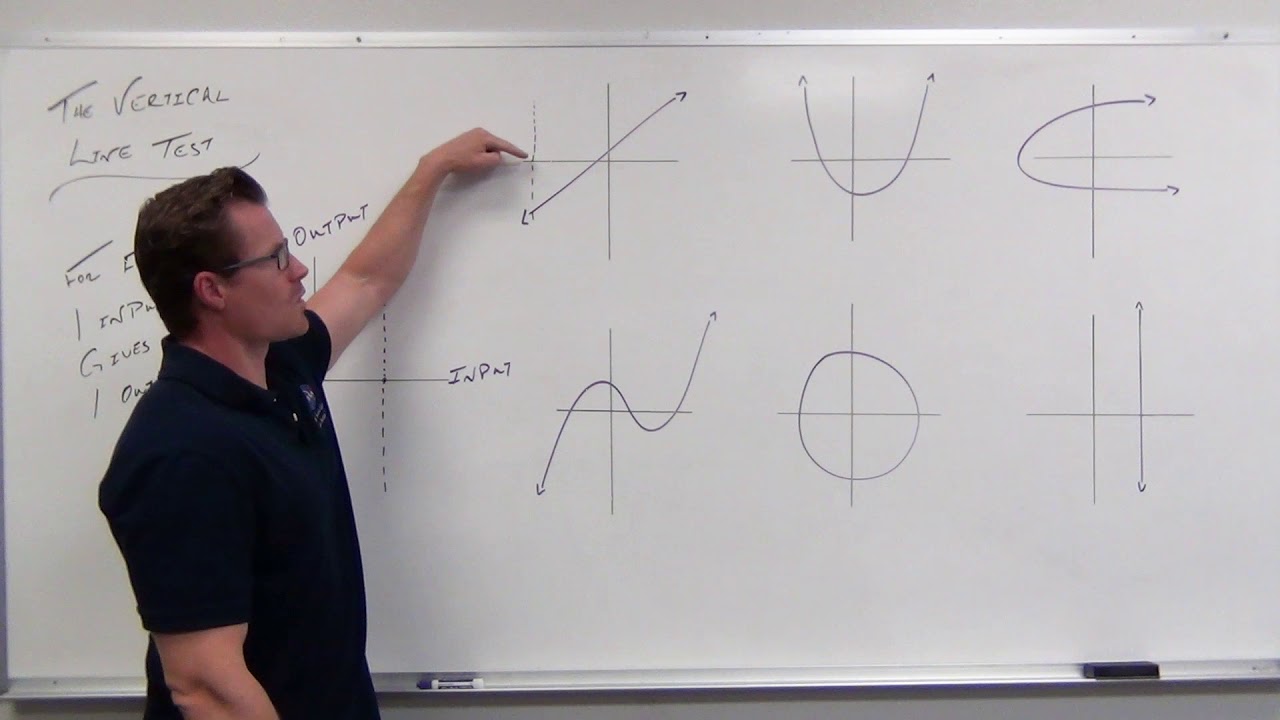
Vertical Line Test

The Organic Chemistry Tutor
8 Feb 201805:27
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the concept of functions in mathematics, specifically focusing on the vertical line test as a method to determine whether a given graph represents a function. By examining various equations, such as linear functions, parabolas, circles, and trigonometric functions, the script explains how a graph passes the test if a vertical line intersects it at only one point. It highlights the importance of this test in discerning true functions from non-functions, thereby aiding in the understanding of mathematical relationships and graphical representations.

Takeaways
  • 📈 The vertical line test is a method to determine if a graph represents a function.
  • 🤔 A graph passes the vertical line test if a vertical line intersects it at only one point.
  • 📊 The linear function y = x is an example of a function, as it forms a straight line and passes the test.
  • 🔢 The equation x = y^2 does not represent a function because a vertical line intersects it at more than one point.
  • 🍃 A parabola y = x^2 passes the vertical line test and is thus a function, as each vertical line intersects the curve at a single point.
  • ⭕ A circle's equation (x^2 + y^2 = constant) does not represent a function, as it intersects a vertical line at two points.
  • 📶 The horizontal line y = 3 represents a function, as it passes the vertical line test by intersecting at only one point.
  • 🔡 A vertical line x = 4 fails the vertical line test, as it intersects any vertical line at an infinite number of points, not representing a function.
  • √ The square root function and the absolute value function both pass the vertical line test and represent functions due to their unique shapes.
  • 🚫 The graph of √x (square root of x) passes the test, while the sine function x (as depicted in the example) does not pass the vertical line test at certain points.
  • 🔢 Functions like x^3 (cubed) and the cube root of x are functions and pass the vertical line test, as indicated by their respective graphs.
Q & A

  • What is the vertical line test used for in the context of functions and graphs?

    -The vertical line test is used to determine whether a graph represents a function. If a vertical line can be drawn that intersects the graph more than once, then the graph does not represent a function. This is because a function, by definition, must have a single output for each input value.

  • How does the vertical line test apply to a linear function like y equals x?

    -For a linear function such as y equals x, if you draw a vertical line, it will intersect the graph at only one point, indicating that the graph represents a function. This is because linear functions are one-to-one, meaning each x-value corresponds to a unique y-value.

  • What happens when you apply the vertical line test to the equation x equals y squared?

    -When applying the vertical line test to the equation x equals y squared, you will find that a vertical line intersects the graph at more than one point. This indicates that the graph does not represent a function, as a function requires that each input value have a unique output value.

  • How can you tell if a parabola like y equals x squared is a function based on the vertical line test?

    -A parabola like y equals x squared will pass the vertical line test because a vertical line will intersect the parabola at only one point. This shows that for each x-value, there is a single corresponding y-value, which is the definition of a function.

  • What is the result of applying the vertical line test to the equation x squared plus y squared equals nine, which represents a circle?

    -The equation x squared plus y squared equals nine represents a circle, and when you apply the vertical line test, the vertical line will intersect the circle at two points. This means the graph is not a function because a function requires that each input value result in a unique output value.

  • How does the vertical line test work for a horizontal line like y equals three?

    -A horizontal line like y equals three will pass the vertical line test because any vertical line drawn on it will intersect at only one point. This is consistent with the definition of a function, as each x-value on the line corresponds to a single y-value.

  • What happens when you apply the vertical line test to a vertical line like x equals four?

    -Applying the vertical line test to a vertical line like x equals four results in failure because a vertical line will intersect it at an infinite number of points. This does not satisfy the criteria for a function, which requires a single output for each input value.

  • How can you determine if the square root of x and the absolute value of x are functions using the vertical line test?

    -Both the square root of x and the absolute value of x can be determined to be functions using the vertical line test because a vertical line will intersect each of these graphs at only one point. This adherence to the one-output-per-input rule confirms that they are indeed functions.

  • Why does the graph of the sine function of x not pass the vertical line test in the given examples?

    -The graph of the sine function of x does not pass the vertical line test in the given examples because it intersects the vertical line at more than one point for a particular line. This indicates that there are multiple output values for at least one input value, violating the definition of a function.

  • How can you confirm that x cubed and the cube root of x are functions using the vertical line test?

    -Both x cubed and the cube root of x can be confirmed as functions using the vertical line test because any vertical line drawn on these graphs will intersect at only one point. This one-to-one correspondence between input and output values is consistent with the definition of a function.

  • What is the conclusion from the video regarding using the vertical line test to identify if a graph represents a function?

    -The conclusion from the video is that the vertical line test is a method to determine if a graph represents a function. If a vertical line intersects the graph more than once, the graph does not represent a function. However, if it intersects at only one point for all vertical lines, then the graph represents a function.

Outlines
00:00
📊 Understanding Functions with the Vertical Line Test

This paragraph introduces the concept of using the vertical line test to determine if a graph represents a function. It explains that a graph passes the test if a vertical line drawn anywhere on the graph touches the graph at only one point. The explanation begins with a linear function (y=x) as an example of a function because it's a straight line that touches a vertical line at a single point. It contrasts this with the equation x=y^2, which is not a function since a vertical line would touch it at more than one point. The paragraph further illustrates the concept with examples of a parabola (y=x^2), a circle (x^2 + y^2 = 9), and a horizontal line (y=3). It also discusses the implications of a vertical line (x=4) and the functions of square root of x and absolute value of x. The paragraph concludes by mentioning the sine function and the functions x^3 and x^(1/3), emphasizing that the latter two pass the vertical line test, while the former does not for a specific graph shown.

05:01
📈 Applying the Vertical Line Test to More Graphs

This paragraph continues the discussion on the vertical line test and its application to various graphs. It challenges the viewer to apply the test to the graphs of the square root of x and the absolute value of x, both of which pass the test as they only touch a vertical line at one point. The paragraph then presents two additional examples for the viewer to consider: the sine function (sin(x)) and the functions x^3 and x^(1/3). It clarifies that while the sine function is generally a function, the specific graph shown does not pass the vertical line test, whereas x^3 and x^(1/3) do pass the test. The paragraph concludes by reinforcing the method of the vertical line test as a way to ascertain whether a given graph represents a function.

Mindmap
Keywords
💡Function
In mathematics, a function is a relation that assigns a single output to each input. It is a way to describe how one quantity changes as another quantity varies. In the context of the video, determining whether a graph represents a function is the main focus. A function is represented by a graph that passes the vertical line test, meaning any vertical line drawn through the graph will intersect at most one point on the graph.
💡Vertical Line Test
The vertical line test is a graphical method used to determine whether a given graph represents a function. According to this test, if any vertical line intersects a graph at more than one point, the graph does not represent a function. The test is based on the definition of a function, which requires that each input (x-value) has exactly one output (y-value).
💡Linear Function
A linear function is a mathematical function that has the form f(x) = mx + b, where m and b are constants, and m is the slope of the line. Linear functions represent straight lines when graphed, and they are one of the simplest types of functions. In the video, y=x is an example of a linear function, which is represented by a straight line on the graph and passes the vertical line test.
💡Parabola
A parabola is a U-shaped curve, which is a graph of a quadratic function. The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants. Parabolas can open upwards or downwards and have a single vertex at their peak or trough. In the video, y=x^2 represents a parabola, which passes the vertical line test as it touches any vertical line at only one point.
💡Circle
A circle is a set of points in a plane that are all at the same distance from a central point, known as the center of the circle. In the context of the video, the equation x^2 + y^2 = 9 represents a circle with a radius of 3, centered at the origin. Circles do not represent functions because they fail the vertical line test; a vertical line will intersect a circle at two points.
💡Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In the context of functions, the square root function is represented by f(x) = √x, and it is increasing on its domain, meaning that as x increases, f(x) also increases. The graph of the square root function is a curve that opens to the right and passes the vertical line test.
💡Absolute Value
The absolute value of a number is the non-negative value of that number without regard to its sign. It is denoted by two vertical lines on either side of the number. The absolute value function is represented by f(x) = |x| and is characterized by a V-shape on a graph. The absolute value function is increasing on its domain and passes the vertical line test.
💡Sine Function
The sine function is a trigonometric function that relates the ratio of the opposite side to the hypotenuse in a right triangle to the angle in that triangle. It is a periodic function that oscillates between -1 and 1 and is represented by the graph of y = sin(x). The sine function does not pass the vertical line test because it intersects any given vertical line at multiple points as it repeats its pattern.
💡Cube Function
The cube function refers to a mathematical function where the independent variable is raised to the third power. The general form is f(x) = x^3. This type of function is not a straight line and can have both positive and negative values. However, the cube function is a function because its graph passes the vertical line test, as each vertical line intersects the graph at most once.
💡Cube Root
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. It is the inverse operation of cubing a number. The cube root function is represented by f(x) = ∛x, and its graph is a curve that is monotonically increasing over its entire domain. The cube root function passes the vertical line test because any vertical line will intersect the graph at only one point.
💡Graph
In mathematics, a graph is a visual representation of the relationship between variables. It is a set of points on a coordinate system, where each point corresponds to a pair of values, one for the x-coordinate and one for the y-coordinate. Graphs are used to visualize functions and equations, and they can help to understand the behavior and properties of these mathematical relationships. The video script discusses various graphs and their ability to represent functions based on the vertical line test.
Highlights

The video discusses the method of using the vertical line test to determine if a graph represents a function.

A linear function, y equals x, is represented by a straight line and passes the vertical line test.

The equation x equals y squared does not represent a function as it fails the vertical line test by touching a vertical line at more than one point.

A parabola, y equals x squared, passes the vertical line test and thus represents a function.

A circle with the equation x squared plus y squared equals nine is not a function because it touches a vertical line at two points.

The vertical line x equals four does not represent a function as it touches a vertical line at an infinite number of points.

The square root of x and the absolute value of x both represent functions as they pass the vertical line test.

The graph of sine x does not pass the vertical line test and therefore is not a function.

The functions x cubed and the cube root of x both pass the vertical line test and are thus considered functions.

Another example is provided to illustrate that a graph touching a vertical line at two points does not represent a function.

The vertical line test is a method to determine if a graph represents a function by checking if any vertical line intersects the graph at most once.

The video provides a comprehensive overview of various mathematical functions and their graphical representations in relation to the vertical line test.

Understanding the vertical line test is crucial for distinguishing between functions and non-functions in graphical analysis.

The video offers clear examples and explanations, making it an educational resource for learning about functions and their graphical interpretations.

The concept of functions and their graphical tests, like the vertical line test, is fundamental in mathematics, particularly in algebra and calculus.

The video's approach to explaining the vertical line test is both systematic and easy to follow, enhancing the viewer's understanding of the topic.

By the end of the video, viewers will have a solid grasp of how to apply the vertical line test to various graphs to ascertain if they represent functions.

The video serves as an effective educational tool for anyone seeking to understand the basics of functions and their graphical analysis.

Transcripts

Browse More Related Video

Using the Vertical Line Test (Precalculus - College Algebra 6)

Ch. 2.2 Graphs of Functions

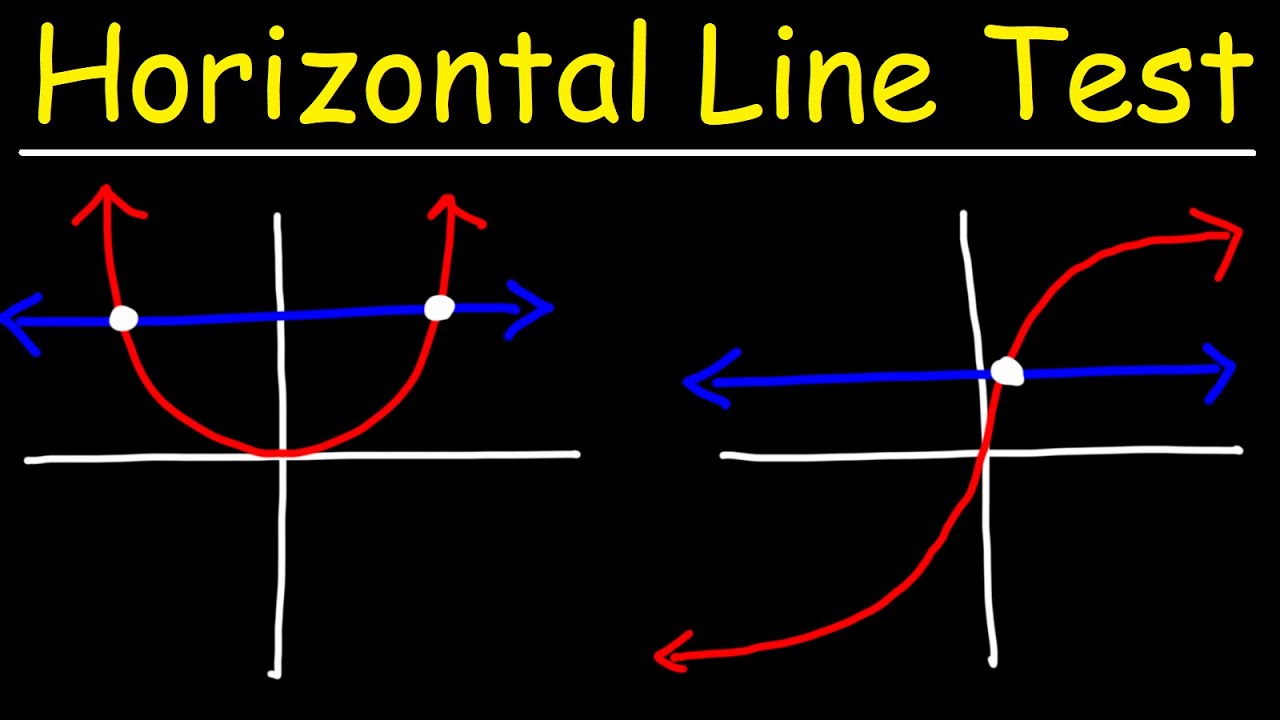
Horizontal Line Test and One to One Functions

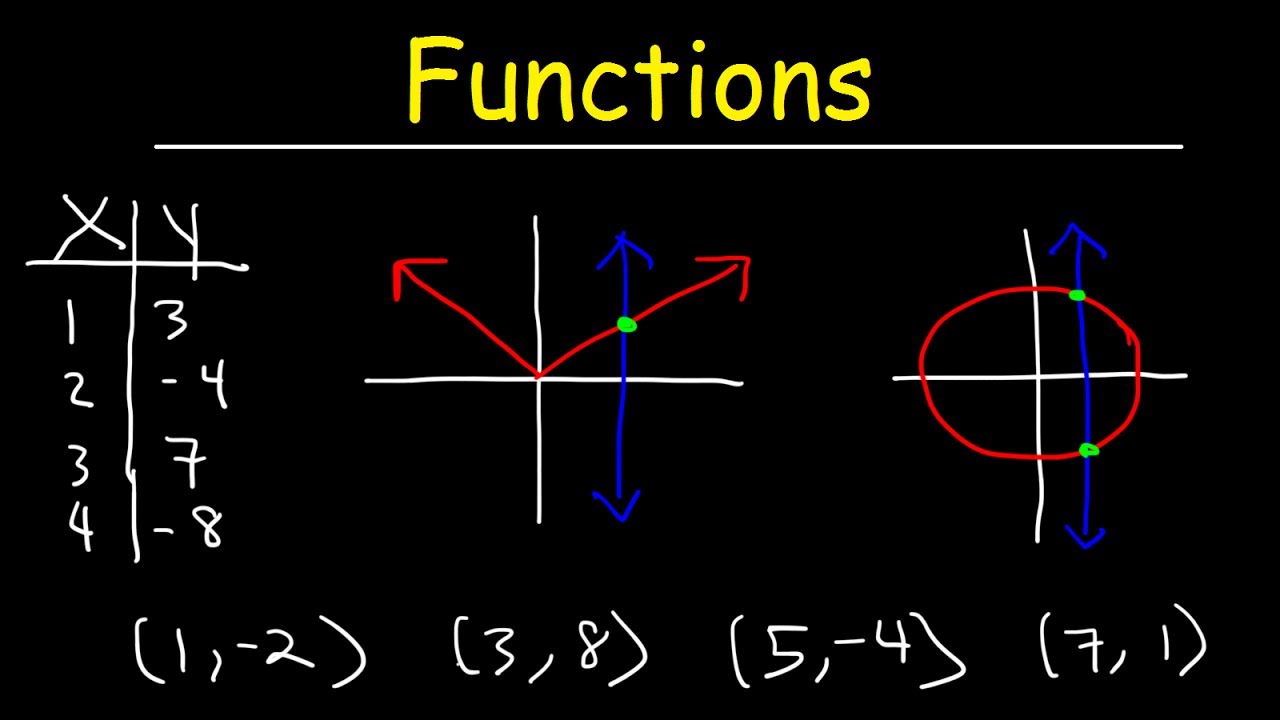
Functions - Vertical Line Test, Ordered Pairs, Tables, Domain and Range

Calculus - Lesson 6 | What are Functions? | Don't Memorise

One to One Functions (Precalculus - College Algebra 50)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsFunctionsVertical Line TestLinear EquationsParabolasCirclesTrigonometryGraph TheoryEducational ContentMath Tutorial