One to One Functions (Precalculus - College Algebra 50)

Professor Leonard
26 Oct 202014:55
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers an insightful exploration into the concept of one-to-one functions, which are fundamental in mathematics for understanding inverse functions. It explains that a one-to-one function is characterized by a unique output for each input, ensuring that the mapping between inputs and outputs is bidirectional. This property is crucial for the existence of inverses, which are essential for mathematical operations like undoing exponentials with logarithms. The script uses the example of employee ID numbers to illustrate the concept and emphasizes the importance of one-to-one functions for the inverse to be meaningful. It also introduces the horizontal line test as a graphical method to determine if a function is one-to-one, complementing the vertical line test used to confirm if a relation is a function. The video concludes by stressing the significance of one-to-one functions in the context of finding inverses, setting the stage for further discussion on the topic in subsequent videos.

Takeaways
  • 📌 A one-to-one function is defined as a function where each input corresponds to a unique output that doesn't repeat.
  • 🔄 The necessity of one-to-one functions arises from the requirement for inverses to exist, which is essential for exploring concepts like exponentials and logarithms.
  • 🧵 The concept of mapping is crucial in one-to-one functions, where each input maps to a unique output and vice versa, maintaining a forward and backward relationship.
  • ❌ If a function is not one-to-one, it fails the horizontal line test, meaning there are repeated outputs for different inputs, which is not allowed for inverses to function properly.
  • 🔍 The horizontal line test is a graphical method to determine if a function is one-to-one by checking if any horizontal line intersects the graph more than once.
  • 📊 The vertical line test is used to verify if a relation is a function, ensuring that no vertical line intersects the graph at more than one point.
  • 🔁 For a function to have an inverse, it must be one-to-one, which means that when inputs and outputs are switched, the resulting relation is also a function.
  • ↕️ The process of finding an inverse involves switching the x and y values, which is only possible if the original function is one-to-one.
  • ✅ Both f(x) and g(x) are functions if their inputs and outputs are unique and do not repeat, but only f(x) is one-to-one based on the given examples.
  • 🚫 A parabola, in general, is not a one-to-one function because it has the same output value for multiple inputs, failing the horizontal line test.
  • 🔑 Understanding one-to-one functions is fundamental to grasp the concept of inverses, which are used to reverse mathematical operations like addition, multiplication, and exponentiation.
Q & A

  • What is a one-to-one function?

    -A one-to-one function is a type of function where each input value maps to a unique output value, ensuring that no two different inputs produce the same output.

  • Why are one-to-one functions important?

    -One-to-one functions are important because they allow for the existence of inverse functions. This means that for every output of a one-to-one function, there is a unique corresponding input, which is necessary for operations like solving exponentials and logarithms.

  • How can you determine if a function is one-to-one by looking at its graph?

    -You can determine if a function is one-to-one by using the horizontal line test. If no horizontal line intersects the graph more than once, the function is one-to-one.

  • What is the vertical line test, and how does it relate to functions?

    -The vertical line test is a graphical method to determine if a curve represents a function. If no vertical line intersects the curve more than once, then the curve passes the vertical line test and represents a valid function.

  • How does the concept of mapping forward and backward apply to one-to-one functions?

    -In a one-to-one function, the concept of mapping forward and backward means that for every input, there is a unique output, and for every output, there is a unique input. This bidirectional mapping ensures that the function is one-to-one.

  • What happens if a function is not one-to-one?

    -If a function is not one-to-one, it means that there are at least two different inputs that produce the same output. Such a function does not have an inverse function because the inverse would not be well-defined (one output would correspond to two inputs).

  • Why do we need inverse functions?

    -We need inverse functions to mathematically 'undo' certain operations. For example, subtraction undoes addition, division undoes multiplication, and logarithms undo exponentiation. Inverse functions are crucial for solving equations and performing various mathematical operations.

  • What is the relationship between the domain and range of a one-to-one function?

    -In a one-to-one function, the domain (set of inputs) and range (set of outputs) have a one-to-one correspondence, meaning each element in the domain maps to a unique element in the range, and vice versa.

  • Can a parabola be a one-to-one function?

    -A parabola is generally not a one-to-one function because it can have multiple inputs corresponding to the same output (e.g., a quadratic function can have two x-values for a single y-value). However, if the domain is restricted, a portion of a parabola can be a one-to-one function.

  • What is the horizontal line test, and how does it help determine if a function is one-to-one?

    -The horizontal line test is a graphical method used to determine if a function is one-to-one. If any horizontal line intersects the graph of the function more than once, the function is not one-to-one because it means there are multiple inputs for the same output.

  • How does the concept of unique outputs relate to the existence of inverse functions?

    -Unique outputs are essential for the existence of inverse functions because if a function has unique outputs for each input, it ensures that when the inputs and outputs are interchanged (as happens with inverse functions), there is a unique input for each output, which is necessary for the inverse to be a function.

Outlines
00:00
📚 Introduction to One-to-One Functions

This paragraph introduces the concept of one-to-one functions, which are essential for understanding inverse functions. A one-to-one function is defined as a function where each input corresponds to a unique output. The importance of one-to-one functions is emphasized for the existence of inverses, which are necessary for exploring mathematical concepts like exponentials and logarithms. The paragraph uses the analogy of employee ID numbers to illustrate the concept of a one-to-one mapping, where each name (input) corresponds to a unique ID number (output), and vice versa.

05:00
🔍 Identifying One-to-One Functions

The second paragraph delves into how to identify whether a given relationship is a one-to-one function by examining the uniqueness of outputs for each input. It explains the horizontal line test, which involves checking if any horizontal line intersects the graph of the function more than once. If it does, the function is not one-to-one because it implies that the same output corresponds to more than one input. The paragraph also discusses the necessity of one-to-one functions for inverses to make sense mathematically, as inverses require a unique mapping between inputs and outputs.

10:01
📈 Graphical Analysis of One-to-One Functions

The final paragraph provides a graphical perspective on one-to-one functions, using the vertical line test to confirm that a relationship is a function and the horizontal line test to determine if it is one-to-one. It explains that for a function to be one-to-one, every potential output (y-value) must intersect the graph at most once, ensuring that each output is unique and corresponds to a single input. The paragraph also discusses why parabolas and horizontal lines cannot represent one-to-one functions due to their nature of producing repeated outputs for different inputs. The importance of understanding one-to-one functions is reiterated in preparation for learning about inverse functions in subsequent videos.

Mindmap
Keywords
💡One-to-One Function
A one-to-one function, also known as an injective function, is a mathematical concept where each input is linked to a unique output, and no two different inputs will produce the same output. This is crucial for the existence of an inverse function. In the video, the concept is illustrated with examples like employee ID numbers, where each name (input) corresponds to a unique ID number (output), ensuring the mapping can be done both ways.
💡Inverse Functions
Inverse functions are mathematical operations that 'reverse' the effect of the original function. If a function takes an input and produces an output, its inverse takes that output and returns the original input. The video emphasizes that only one-to-one functions have inverses because they ensure a unique mapping between inputs and outputs, which is necessary for the inverse to be well-defined.
💡Unique Output
Unique output refers to the property where each input to a function corresponds to a distinct output. This is a defining characteristic of one-to-one functions. In the video, the uniqueness is highlighted as essential for the function to be invertible. An example used is that of ID numbers assigned to employees, where no two employees share the same ID number.
💡Vertical Line Test
The vertical line test is a graphical method to determine if a curve represents a function. According to the video, if any vertical line intersects the curve more than once, the curve does not represent a function because functions require each input to have exactly one output. All the graphs discussed in the video pass the vertical line test, indicating they are all functions.
💡Horizontal Line Test
The horizontal line test is another graphical method used to determine if a function is one-to-one. If a horizontal line intersects the graph of the function more than once, the function is not one-to-one because it implies that the same output corresponds to more than one input. In the video, it is used to analyze the given graphs and determine which of them represent one-to-one functions.
💡Exponentials and Logarithms
Exponentials and logarithms are mathematical operations that are inverses of each other. Exponential functions deal with constant bases raised to varying powers, while logarithms are the inverse operation that finds the power to which the base must be raised to produce a given number. The video mentions that understanding one-to-one functions is essential for exploring these concepts because they are inherently one-to-one and thus have inverses.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The video script clarifies that a function is defined by the rule that one input gives you one output. This basic concept is extended to one-to-one functions, which are a subset of functions with the additional property that each output is unique.
💡Mapping
Mapping in the context of functions refers to the process of assigning outputs to inputs. A one-to-one function ensures a bijective mapping, meaning each input maps to a unique output and vice versa. The video uses the analogy of employee names to ID numbers to illustrate this concept, emphasizing that a one-to-one mapping is required for the inverse function to exist.
💡Non-One-to-One Function
A non-one-to-one function, also known as a non-injective function, is one where an output can be associated with more than one input. This is demonstrated in the video with an example where two employees share the same ID number, which would not allow for a unique reverse mapping and hence, no inverse function. The video explains that such functions fail the horizontal line test.
💡Domain and Range
In the context of functions, the domain refers to the set of all possible inputs for a function, while the range (or output) is the set of all possible outputs. The video touches on the idea that for a function to be one-to-one, its domain must be such that no two different inputs result in the same output, ensuring uniqueness across the range.
💡Graphical Representation
Graphical representation is a method of visually depicting the relationship between inputs and outputs of a function using a graph. In the video, graphical representation is used to illustrate the concepts of one-to-one functions, vertical and horizontal line tests, and to visually confirm whether a function has an inverse. The graphs of functions are plotted with the x-axis representing inputs and the y-axis representing outputs.
Highlights

The introduction of one-to-one functions and their importance in the context of inverse functions.

Explanation that a one-to-one function is defined by one input giving one unique output.

The necessity of one-to-one functions for the existence of inverses, which is crucial for exploring exponentials and logarithms.

The concept of mapping forward and backward in one-to-one functions, exemplified by employee ID numbers.

The scenario where non-unique outputs lead to confusion in practical applications, like ID number conflicts.

The explanation of the vertical line test to determine if a set of points represents a function.

The introduction of the horizontal line test as a method to identify one-to-one functions.

The graphical representation of functions and how they pass the vertical line test to be considered functions.

The graphical analysis of functions to determine if they are one-to-one based on the horizontal line test.

The explanation that a function must be both a function (each input has one output) and one-to-one (each output is unique) to have an inverse.

The example of a non-one-to-one function where the same output is repeated for different inputs.

The importance of one-to-one functions in mathematical operations, such as how inverses undo their respective operations.

The assertion that only one-to-one functions have inverses, and if a function has an inverse, it must be one-to-one.

The brief overview of the content and the anticipation of further discussion on algebraic looks of functions in future videos.

Transcripts

Browse More Related Video

Finding Inverse Functions (Precalculus - College Algebra 51)

Ch. 2.8 One-to-One Functions and their Inverses

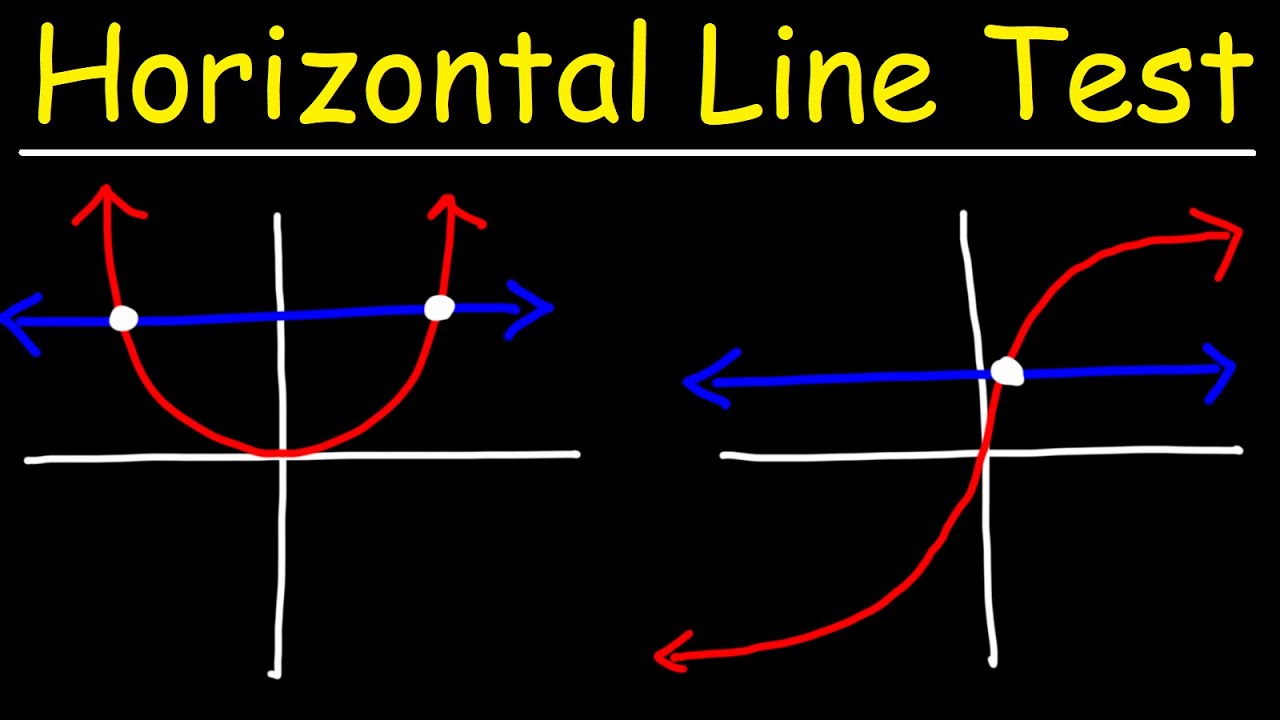
Horizontal Line Test and One to One Functions

Introduction to Inverse Trigonometric Functions (Precalculus - Trigonometry 17)

Functions

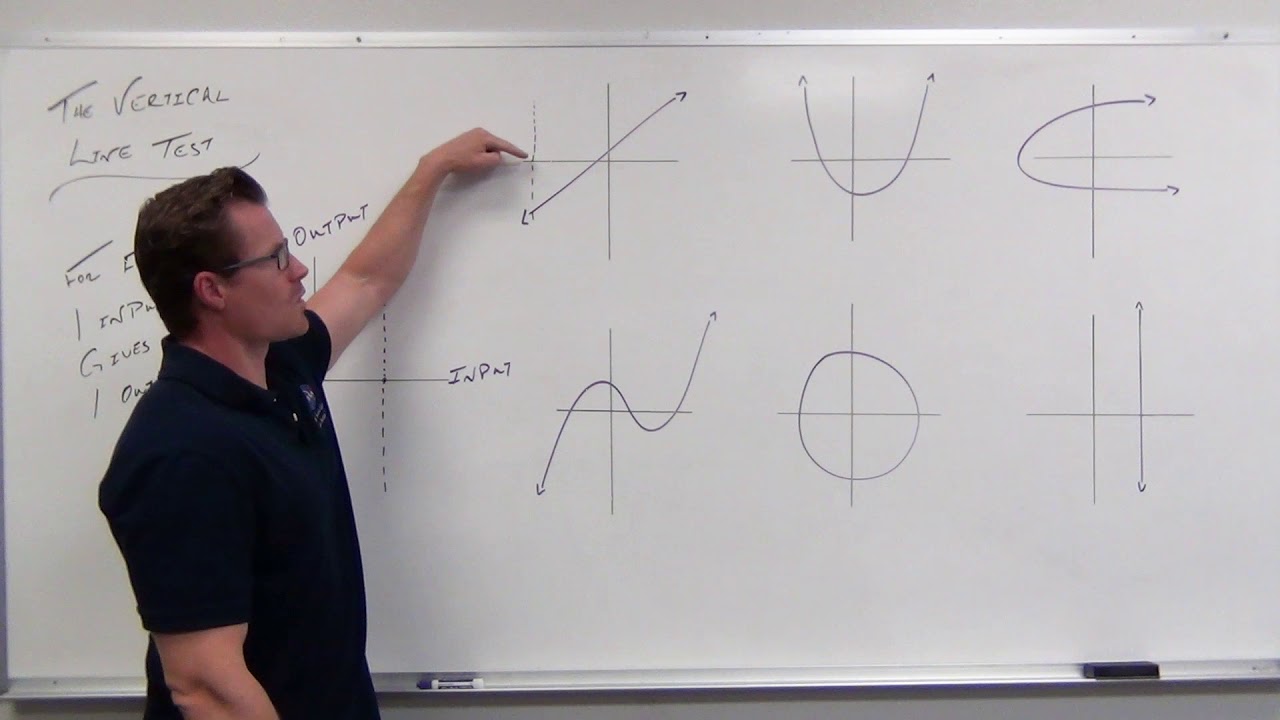
Using the Vertical Line Test (Precalculus - College Algebra 6)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
One-to-One FunctionsInverse FunctionsMathematical ConceptsExponentialsLogarithmsFunction PropertiesUnique OutputsInput-Output MappingVertical Line TestHorizontal Line TestMath Education