1.8 - Higher Order Derivatives
TLDRThis video script offers an in-depth exploration of higher order derivatives, a fundamental concept in calculus. It explains that these derivatives are created by differentiating a function's derivative, leading to a sequence of derivatives that can simplify or complicate the original function. The script delves into various notations for representing these derivatives, including the use of primes and superscripts. It also discusses the practical applications of derivatives in physics, such as determining an object's velocity and acceleration from its position over time, and in business, like analyzing sales trends over months. The video provides step-by-step examples of finding higher order derivatives for different functions, emphasizing the importance of understanding not just the process but also the meaning behind each derivative in context.
Takeaways
- 📌 Higher-order derivatives are obtained by differentiating the derivative of a function, which can simplify or complicate the function depending on its structure.
- 📝 Notation for higher-order derivatives can include additional primes (e.g., f''(x) for the second derivative) or a superscript number in parentheses (e.g., f^(4)(x) for the fourth derivative).
- 🔢 The Leibniz notation uses superscripts next to the 'd' to indicate higher-order derivatives (e.g., d^2y/dx^2 for the second derivative).
- 📈 The second derivative specifically indicates how quickly the first derivative is changing, which can be thought of as the rate of change of the rate of change.
- 🧮 Differentiation can be applied indefinitely to generate as many derivatives as desired, each providing insight into the function's behavior.
- 📚 When differentiating, the power rule is commonly used, which involves bringing down the exponent and decreasing it by one for each differentiation step.
- 🤔 The effect of repeated differentiation varies; it can simplify the function by reducing the power of the variable or complicate it by increasing the complexity of the expression.
- 🚀 An example of a practical application of derivatives is in physics, where the first derivative of position with respect to time gives velocity, and the second derivative gives acceleration.
- 📉 In business applications, the first derivative of a sales function can indicate the rate of change in sales over time, while the second derivative can suggest how that rate of change is itself changing.
- 🔑 The chain rule is essential for differentiating more complex functions, such as those involving nested functions, and can lead to increasingly complicated derivatives with each successive differentiation.
- 📘 When evaluating derivatives at specific points, it's crucial to understand not just the mathematical procedure but also the context and the meaning of the derivative in that context.
Q & A
What is a higher order derivative?
-A higher order derivative is a derivative of a derivative. It is obtained by differentiating the original function, then differentiating the result, and so on, to obtain second, third, fourth, and further derivatives. Each differentiation results in a new function that can itself be differentiated.
How is the second derivative of a function represented using prime notation?
-The second derivative of a function is represented with an additional prime mark. For a function f(x), the first derivative is denoted as f'(x), and the second derivative is denoted as f''(x) or sometimes with a subscript number, like f^(2)(x).
What is the meaning of the second derivative in the context of a function's graph?
-The second derivative of a function represents the rate of change of the first derivative. It tells us how quickly the slope (first derivative) is changing as we move along the function's graph.
How does the process of differentiation affect the complexity of a function over time?
-Differentiation can either simplify or complicate a function over time, depending on the original structure of the function. For some functions, repeated differentiation results in simpler functions, while for others, it may lead to more complex expressions.
What is the Leibniz notation for derivatives?
-Leibniz notation is an alternative way to represent derivatives, using differentials d. For instance, the first derivative of y with respect to x is written as dy/dx. Higher order derivatives in Leibniz notation use superscripts to indicate the order, such as d^2y/dx^2 for the second derivative.
What is the physical interpretation of the first and second derivatives when considering an object's distance traveled over time?
-The first derivative of distance with respect to time represents velocity, which is the rate of change of distance. The second derivative represents acceleration, which is the rate of change of velocity. In physics, this is a common application of derivatives to describe motion.
How does the pattern of differentiation affect the exponents in the function y = 1/x?
-In the function y = 1/x, rewriting it as y = x^(-1) and differentiating repeatedly shows a pattern where the exponent of x in the denominator increases with each derivative. The first derivative has x^(-2), the second has x^(-3), and so on.
What is the chain rule and when is it used in differentiation?
-The chain rule is a method used in calculus to differentiate composite functions, which are functions composed of two or more functions. It is used when a function is nested inside another function, and it allows you to differentiate the outer function first and then multiply by the derivative of the inner function.
How does the structure of a function influence the outcome of its successive derivatives?
-The structure of the original function greatly influences the outcome of its successive derivatives. Polynomial functions with decreasing exponents tend to simplify with differentiation, while functions with nested structures or requiring the chain rule can become more complex with each derivative.
What is the application of higher order derivatives in a business context?
-In a business context, higher order derivatives can be used to analyze the rate of change in sales over time. The first derivative represents the change in sales per month, the second derivative indicates how this rate of change is changing, and further derivatives could provide insights into the stability or predictability of sales trends.
How can the second derivative be interpreted in terms of a business's sales trend?
-The second derivative in a business context, such as sales over time, indicates the rate at which the rate of change (first derivative) is changing. A negative second derivative suggests that the rate of change (increase or decrease in sales) is itself decreasing, which could imply that sales are starting to level out or become more predictable.
Outlines
📚 Introduction to Higher Order Derivatives
The video begins by introducing higher order derivatives, which are obtained by differentiating a derivative. It explains that this process can be continued indefinitely, yielding a sequence of derivatives that can simplify or complicate the original function depending on its structure. The notation for higher order derivatives is also discussed, including the use of primes and superscripts to denote the order of the derivative.
📝 Derivative Notation and Practice
This paragraph delves into the notation of derivatives, highlighting the use of primes and superscripts to indicate the order of the derivative. It also contrasts the common notations: prime notation and Leibniz notation. A practical example is given to demonstrate the process of finding the first six derivatives of a polynomial function, illustrating how differentiation can simplify the function over time.
🌟 The Meaning of the Second Derivative
The video explains the significance of the second derivative, which measures how quickly the first derivative (or rate of change) is changing. It uses the analogy of the slope of a tangent line to a function to clarify this concept. A practice problem is presented to find the first and second derivatives of a given function, emphasizing the process and the interpretation of the results.
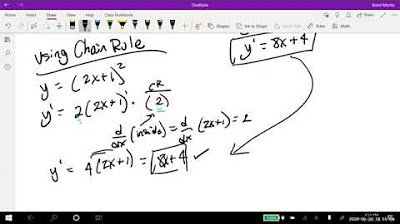
🔗 Chain Rule and Nested Functions
The script addresses the concept of nested functions and the necessity of using the chain rule to differentiate them. It breaks down the steps required to apply the chain rule, including identifying the external and internal functions and their respective derivatives. An example is provided to demonstrate the differentiation process of a nested function, emphasizing the importance of simplifying expressions.
📈 Simplifying Derivatives with Common Factors
The paragraph focuses on the process of simplifying derivatives by identifying and factoring out common terms. It discusses the importance of arranging terms in a logical order and combining like terms. The example continues from the previous paragraph, showing how to further simplify the derivative of a nested function by factoring out common factors and coefficients.
🚀 Applications of Higher Order Derivatives
This part of the video explores the applications of higher order derivatives, particularly in physics and business contexts. It explains how the first derivative represents velocity, the second derivative represents acceleration, and how these concepts can be applied to problems involving distance over time. An example involving a stone falling is used to illustrate these principles.
📊 Business Application of Derivatives
The script concludes with a business-oriented application of derivatives, where the focus is on analyzing the sales of a company over time. It outlines how to calculate and interpret the first and second derivatives of a sales function, providing insight into how the rate of change of sales (revenue growth) is accelerating or decelerating at different points in time.
🎓 Interpretation of Derivatives in Context
The final paragraph emphasizes the importance of interpreting the values obtained from derivatives in the context of the problem. It explains that the first derivative indicates the rate of change (e.g., increasing or decreasing sales), while the second derivative indicates how that rate of change is itself changing (e.g., the acceleration or deceleration of sales growth). The example provided shows how the interpretation of derivatives can offer insights into business performance over time.
Mindmap
Keywords
💡Higher Order Derivatives
💡Notation
💡Derivative
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Power Rule
💡Instantaneous Rate of Change
💡Velocity and Acceleration
💡Position Function
💡Business Application
Highlights
Higher order derivatives are generated by taking the derivative of a derivative, leading to first, second, third, and so on.
Differentiation is a process that can be completed indefinitely, creating new functions each time.
Notation for higher order derivatives includes using additional primes (e.g., f''(x) for second derivative) or a superscript number (e.g., f^(4)(x)).
Leibniz notation uses superscripts next to the 'd' to indicate higher order derivatives (e.g., d^2y/dx^2 for second derivative).
The second derivative indicates how fast the first derivative is changing, providing insight into the rate of change of the slope of a function at different points.
Differentiating a polynomial function can simplify the function over time by reducing the exponents.
The derivative of a constant is always zero, which is observed when differentiating repeatedly and the function simplifies to a constant.
For the function y = 1/x, rewriting 1/x as x^(-1) simplifies differentiation using the power rule rather than the quotient rule.
Differentiation of nested functions, like y = (x^2 + 10x)^20, requires the use of the chain rule and can result in increasingly complex derivatives.
The product rule is essential when differentiating the second derivative of a nested function, as it involves differentiating a product of two functions.
Rearranging terms and factoring out common factors can simplify the process of differentiating and finding higher order derivatives.
In physics, the first derivative of position with respect to time represents velocity, while the second derivative represents acceleration.
For an object in free fall, the distance function s(t) = 4.905t^2 can be differentiated to find velocity and acceleration at any given time t.
In business applications, derivatives can help analyze how sales are changing over time, with the first derivative indicating the rate of change in sales and the second derivative indicating how that rate is changing.
The second derivative can indicate whether a quantity, like sales or velocity, is increasing, decreasing, or leveling off by analyzing the sign and changes in the second derivative's value.
Repeated differentiation can provide insights into the behavior of functions over time, with practical applications in physics and business analytics.
The process of differentiating a function multiple times can reveal simplification or increasing complexity, depending on the original function's structure.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: