Volume with cross sections: triangle | AP Calculus AB | Khan Academy
TLDRThe video script discusses the process of visualizing and calculating the volume of a three-dimensional figure with a base defined by the intersection of two graphs, y=f(x) and y=g(x). The figure is described as having isosceles right triangular cross sections, and the volume is approximated by summing the volumes of these individual triangles. The final expression for the volume is given as a definite integral from x=0 to x=c of (1/4) * (F(x) - G(x))^2 dx, highlighting the intersection points at (0,0) and (c,d).
Takeaways
- 📊 The discussion revolves around visualizing a three-dimensional shape with a base defined by the graphs of Y=F(X) and Y=G(X).
- 🎨 The base of the shape is represented by a shaded region in a specific color (mauve or purple) and appears to pop out of the screen.
- 🔵 A blue line represents the top ridge of the figure, and cross sections are perpendicular to the X-axis.
- 🟨 The cross sections are isosceles right triangles, and when flattened, they maintain the same shape and proportions.
- 📐 The hypotenuse of each isosceles right triangle aligns with the base of the figure, and the equal distances between points on the base correspond to the difference between F(X) and G(X).
- 📈 A coordinate plane is drawn to help visualize the figure from an overhead perspective, with the base and other sides clearly delineated.
- 🤔 The challenge is to derive a definite integral expression that describes the volume of the figure, which has a unique shape akin to a football or rugby ball.
- 🌟 The figure intersects the coordinate plane at specific points (0,0) and (c,d), which are crucial for the integral calculation.
- 📂 The volume is approximated by considering the volume of individual triangles, which is the cross-sectional area times a small depth (dx).
- 📝 The area of each isosceles right triangle is calculated as one-fourth the square of the hypotenuse (H), which is derived from the Pythagorean theorem.
- 🧮 The volume of the entire figure is found by integrating the volume of these triangles from X=0 to X=C, resulting in the definite integral (∫ from X=0 to X=C) of (1/4)H^2 dx.
Q & A
What is the base of the three-dimensional shape described in the script?
-The base of the shape is the shaded region between the graphs of Y = F(X) and Y = G(X).
How are the cross sections of the figure described?
-The cross sections of the figure are isosceles right triangles that are perpendicular to the X-axis.
What is the relationship between the hypotenuse of the isosceles right triangle and the base of the figure?
-The hypotenuse of the isosceles right triangle sits along the base of the figure, and its length is equal to the distance between F(X) and G(X) for a given X value.
How does the distance between the points on the hypotenuse change as X values change?
-The distance between the points on the hypotenuse changes as the X values change because F(X) and G(X) are functions of X, thus altering the lengths and positions of the cross sections.
What is the purpose of the coordinate plane drawing in the script?
-The coordinate plane drawing helps visualize the figure from different angles, particularly from above, to better understand its structure and shape.
How is the volume of the individual triangles in the figure approximated?
-The volume of the individual triangles is approximated by calculating the area of the cross-sectional isosceles right triangle and multiplying it by a very small depth (DX).
What is the expression for the height (H) of the isosceles right triangle in terms of X?
-The height (H) of the isosceles right triangle is given by the function H(X) = F(X) - G(X).
How can the area of the isosceles right triangle be calculated using the Pythagorean theorem?
-The area of the isosceles right triangle can be calculated by recognizing that the sides of the triangle are in a 1:1 ratio to the hypotenuse (A = H/√2), and the area is 1/2 * base * height, which in this case is 1/4 * H^2.
What is the volume of a single triangle in the figure?
-The volume of a single triangle is the area of the cross-sectional isosceles right triangle multiplied by the depth (DX), which is 1/4 * H^2 * DX.
How can the volume of the entire figure be expressed as a definite integral?
-The volume of the entire figure can be expressed as the definite integral from X=0 to X=C of 1/4 * (F(X) - G(X))^2 * DX.
What is the significance of the intersection points of the functions F(X) and G(X) in the context of the volume calculation?
-The intersection points of F(X) and G(X) are significant because they define the limits of the definite integral that calculates the volume of the figure, specifically from the origin (0,0) to the point (C,D).
Outlines
📊 Visualizing a 3D Shape with Intersecting Functions
The paragraph begins with a voiceover introducing the concept of visualizing a three-dimensional shape, whose base is defined by the intersection of two graphs: Y = f(X) and Y = g(X). The speaker describes the base as a shaded region and explains that the top ridge of the figure can be represented by a blue line. The cross sections of the figure, perpendicular to the X-axis, are isosceles right triangles. The speaker provides a detailed explanation of how these cross sections would look when flattened out and relates the dimensions of these triangles to the functions' intersection points. The main goal of this part of the script is to help the audience visualize the shape and set the stage for finding a definite integral that describes the volume of the figure, which is compared to a football or rugby ball. The speaker encourages the audience to use the information that the functions intersect at the points (0,0) and (c,d) to come up with an expression for the volume.
📐 Calculating the Volume of the 3D Shape
In this paragraph, the speaker delves into the process of calculating the volume of the previously described 3D shape. The speaker suggests approximating the volume by considering the volume of individual triangles, which is the area of the cross section multiplied by a small depth (denoted as DX). The height (H) of the triangle is defined as the difference between the functions, F(X) - G(X). The speaker then explains how to find the area of an isosceles right triangle using the Pythagorean theorem and arrives at the area being one-fourth H squared. The volume of each triangle is found by multiplying the area by the depth DX. The speaker then describes how integrating these volumes from X equals zero to X equals C will give the volume of the entire figure. The final expression for the volume is presented as a definite integral from X equals zero to X equals C of (F(X) - G(X)) squared DX.
Mindmap
Keywords
💡Three-dimensional shape
💡Graphs
💡Cross sections
💡Coordinate plane
💡Definite integral
💡Volume
💡Isoceles right triangle
💡Hypotenuse
💡F(X) and G(X)
💡Intersection points
💡Depth (DX)
Highlights
Imagining a three-dimensional shape with a base as the shaded region between the graphs of Y=F(X) and Y=G(X).
The figure is visualized as popping out of the screen with the top ridge drawn in blue.
Cross sections of the figure are isosceles right triangles perpendicular to the X-axis.
The figure is akin to a football or rugby ball when cut in half, but skewed.
A definite integral is sought to describe the volume of the three-dimensional figure.
The figure intersects at the points (0,0) and (c,d), which is key to formulating the integral.
Volume approximation involves considering the volume of individual triangles.
The height (H) of the triangle is defined as F(X) - G(X).
The area of the isosceles right triangle is derived from the Pythagorean theorem.
The area of the triangle is calculated as one-fourth H squared.
The volume of each triangle is the area times a small depth (DX).
The volume of the entire figure is found by integrating the volumes of the triangles from X=0 to X=C.
The definite integral expression for the volume is ∫ from X=0 to X=C of (1/4)(F(X) - G(X))^2 dX.
The process demonstrates a method for visualizing and calculating the volume of complex geometric shapes.
The explanation emphasizes the importance of understanding cross sections and their geometric properties.
The integration of geometry and calculus provides a powerful tool for describing physical objects.
The session concludes with the successful derivation of a definite integral for the volume of the figure.
Transcripts
Browse More Related Video

Volume with cross sections: squares and rectangles (no graph) | AP Calculus AB | Khan Academy
2015 AP Calculus AB Free Response #2

Volume with cross sections: semicircle | AP Calculus AB | Khan Academy

Solid of Revolution (part 4)
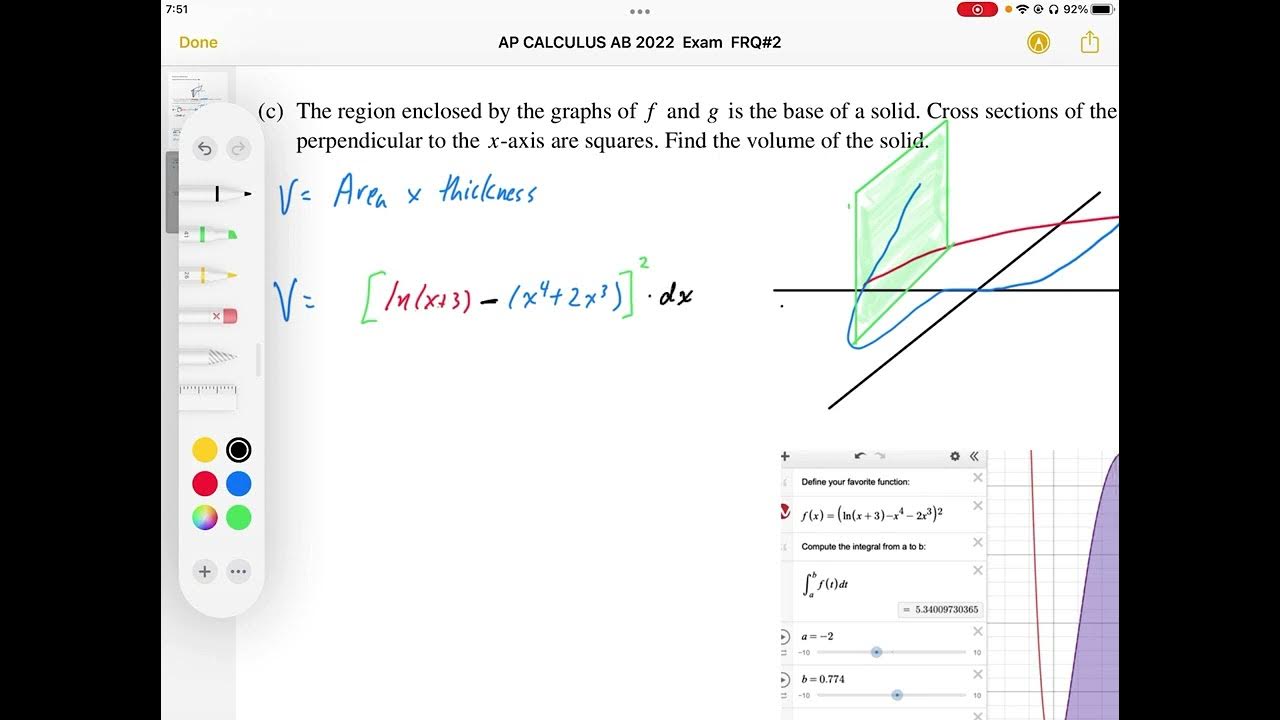
AP CALCULUS AB 2022 Exam Full Solution FRQ#2c

2011 Calculus AB free response #3 (c) | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: