Volume with cross sections: squares and rectangles (no graph) | AP Calculus AB | Khan Academy

Khan Academy
2 Oct 201805:57
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the process of finding the volume of a solid with a specific geometric shape using definite integrals. The solid's base is outlined by the graphs of y = -x^2 + 6x - 1 and y = 4. The cross sections perpendicular to the x-axis are rectangles with height x. The instructor explains how to visualize the graphs to find the intersection points (x=1 and x=5), which define the limits for the integral. The volume is then calculated by integrating the area of the cross sections from x=1 to x=5, using the formula (base area) * height * dx, where the base area is given by the difference in the two y-values, resulting in the integral ∫ from 1 to 5 of (-x^2 + 6x - 5) dx.

Takeaways
  • 📈 The base of the solid is enclosed by the graphs of y = -x^2 + 6x - 1 and y = 4.
  • 🤔 Cross sections of the solid perpendicular to the x-axis are rectangles with height equal to x.
  • 🔍 To find the volume, express it with a definite integral over the interval from x=1 to x=5.
  • 📊 The intersection points of the two graphs are found by setting -x^2 + 6x - 1 equal to 4.
  • 🧠 Solving the equation -x^2 + 6x - 5 = 0 gives the x-values where the solid's cross sections change height.
  • ✅ The factors of the quadratic equation are (x - 1) and (x - 5), indicating the parabola opens downward.
  • 🌐 The vertex of the parabola is at x = 3, which is the midpoint between the intersection points.
  • 📐 The width of the cross sections is determined by the difference in the y-values of the two functions.
  • 🔢 The volume element is given by the base area (negative x squared plus six x minus five) times the height (x) times the infinitesimal depth (dx).
  • 🌠 The definite integral represents the sum of all volume elements from x = 1 to x = 5 to find the total volume of the solid.
  • 📝 The integral is solvable by distributing x and taking the antiderivative of the resulting polynomial.
Q & A

  • What is the region enclosed by the given graphs?

    -The region enclosed is defined by the graphs of y = -x^2 + 6x - 1 and y = 4.

  • How are the cross sections of the solid described in relation to the x-axis?

    -The cross sections of the solid are perpendicular to the x-axis and are rectangles with a height equal to x.

  • What is the equation that represents the intersection of the two given lines?

    -The intersection of the two lines is found by setting -x^2 + 6x - 1 equal to 4.

  • What are the x-values where the two lines intersect?

    -The two lines intersect at x = 1 and x = 5.

  • What is the vertex of the parabola described by the equation -x^2 + 6x - 1?

    -The vertex of the parabola is at x = 3.

  • How can the volume of the solid be expressed using a definite integral?

    -The volume of the solid can be expressed as a definite integral from x = 1 to x = 5 of the function (base) (-height) * dx, where the base is given by -x^2 + 6x - 5.

  • What is the width of the rectangle in the cross section of the solid?

    -The width of the rectangle in the cross section is determined by the difference between the upper function (-x^2 + 6x - 1) and the lower function (4), which simplifies to -x^2 + 6x - 5.

  • How is the volume of the solid calculated?

    -The volume is calculated by multiplying the base of the cross section (negative x squared plus six x minus five) by the height (x) and the infinitesimal depth (dx), then integrating from x equals one to x equals five.

  • What is the significance of the definite integral in calculating the volume?

    -The definite integral allows us to sum up the infinitesimally small volumes of all the cross sections from x equals one to x equals five, giving us the total volume of the solid.

  • How can the antiderivative of the polynomial resulting from the integration be found?

    -The antiderivative of the polynomial can be found by applying the rules of integration to each term of the polynomial, which does not require a calculator and can be done analytically.

Outlines
00:00
📐 Visualizing the Solid and Finding Intersection Points

The paragraph begins with the instructor explaining the task of finding the volume of a solid with a given base and cross sections. The base is defined by the graphs of y = -x^2 + 6x - 1 and y = 4. The cross sections perpendicular to the x-axis are rectangles with height equal to x. The goal is to express the volume using a definite integral. The instructor suggests visualizing the graphs to understand the region better and to find where the two lines intersect. By setting the equations equal to each other and solving for x, the intersection points are found to be x = 1 and x = 5. The paragraph discusses the shape of the parabola and identifies the vertex at x = 3. The visualization of the solid and the base are described, and the process of finding the width of the cross sections is explained. The volume calculation involves multiplying the height (x) by the width (the difference between the two functions) and integrating over the interval from x = 1 to x = 5.

05:02
📚 Integrating to Find the Volume

In this paragraph, the focus is on integrating the cross sections to find the volume of the solid. The instructor describes how to visualize cross sections at different x values and how these sections would look with varying heights. The process of integrating from x = 1 to x = 5 is outlined, emphasizing that the integral involves a polynomial that can be easily solved without a calculator. The definite integral represents the sum of all the cross sections' volumes, and the paragraph concludes with the expression of the solid's volume as a definite integral.

Mindmap
Keywords
💡Solid
In the context of the video, a solid refers to a three-dimensional geometric shape. The base of this solid is defined by the region enclosed by the graphs of two equations: y = -x^2 + 6x - 1 and y = 4. The solid is created by considering cross sections perpendicular to the x-axis, which are rectangles whose height is determined by the variable x.
💡Definite Integral
A definite integral is a mathematical concept used to calculate the signed area under a curve, or in this case, the volume of a solid. It is expressed as the limit of a sum of rectangles as the width of the rectangles approaches zero. In the video, the volume of the solid is found by setting up a definite integral from x = 1 to x = 5 of the function -x^2 + 6x - 5.
💡Graphs
Graphs in this context are visual representations of functions or equations. The video discusses the graphs of two functions: y = -x^2 + 6x - 1 and y = 4. These graphs are used to determine the base of the solid and to find the points of intersection, which are crucial for setting up the definite integral that will be used to find the volume.
💡Intersection
An intersection in mathematics refers to the point or set of points at which two lines, curves, or surfaces meet. In the video, the intersection is used to find the limits of integration, which are the x-values where the two given equations meet the horizontal line y = 4.
💡Vertices
A vertex is a point where two lines or edges meet at an angle. In the context of the video, the vertex of the parabola is the highest or lowest point on the curve. The vertex helps to understand the shape of the solid and is used to find the midpoint between the two intersection points.
💡Cross Sections
Cross sections are cuts or slices through an object that show its internal structure. In the video, the cross sections of the solid are rectangles whose height is given by the variable x and whose width is determined by the difference between the two given equations at any given x-value.
💡Height
In the context of the video, height refers to the vertical dimension of the cross sections of the solid. The height is given by the variable x and is used in the calculation of the volume of the solid through the definite integral.
💡Width
Width in this context refers to the horizontal dimension of the cross sections of the solid. The width is determined by the difference between the upper and lower functions at any given x-value, which is used to calculate the area of each cross section.
💡Volume
Volume is a measure of the amount of space occupied by a solid object. In the video, the volume of the solid is calculated using a definite integral, which sums up the infinitesimal volumes of all the cross sections between the two intersection points of the graphs.
💡Antiderivative
The antiderivative is a function whose derivative is equal to a given function. In the context of the video, finding the antiderivative of the function -x^2 + 6x - 5 is necessary to evaluate the definite integral and thus determine the volume of the solid.
💡Polynomial
A polynomial is an algebraic expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. In the video, the function -x^2 + 6x - 5 is a polynomial, which is used to describe the width of the cross sections of the solid and is integrated to find the volume.
Highlights

The base of the solid is enclosed by the graphs of y = -x^2 + 6x - 1 and y = 4.

Cross sections of the solid perpendicular to the x-axis are rectangles with height equal to x.

The volume of the solid is to be expressed using a definite integral.

To find the intersection points of the two graphs, set -x^2 + 6x - 1 equal to 4.

Solving for x gives us the quadratic equation x^2 - 6x + 5 = 0.

The solutions to the quadratic equation are x = 1 and x = 5, representing the intersection points.

The parabola is downward-opening due to the negative coefficient of the x^2 term.

The vertex of the parabola is at x = 3, midway between the intersection points.

Visualization of the solid helps in understanding the region of integration.

The y-value of the vertex is found by substituting x = 3 into the equation, yielding y = 8.

The base of the solid is defined by the region between the parabola and the line y = 4.

The width of the cross sections is determined by the difference of the two functions.

The volume is calculated by multiplying the height (x) by the width (-x^2 + 6x - 5) and integrating over the interval from x = 1 to x = 5.

The definite integral represents the sum of the volumes of infinitesimally small slices of the solid.

The integral is solvable without a calculator by taking the antiderivative of the polynomial resulting from the multiplication of x with the integrand.

The process demonstrates the application of definite integrals in calculating the volume of a solid with a known cross-sectional shape.

Transcripts

Browse More Related Video

2022 AP Calculus BC Exam FRQ #5

Volume with cross sections: triangle | AP Calculus AB | Khan Academy

Disc method around x-axis | Applications of definite integrals | AP Calculus AB | Khan Academy

Volume with cross sections: intro | Applications of integration | AP Calculus AB | Khan Academy

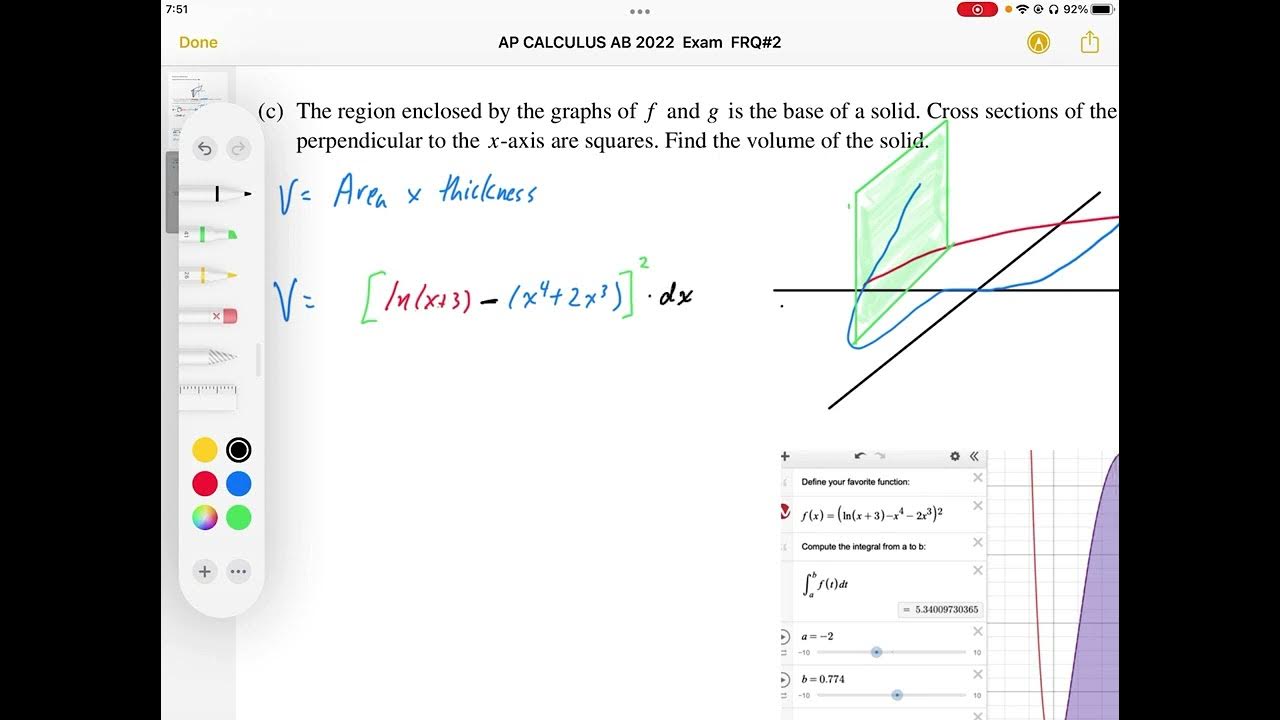
AP CALCULUS AB 2022 Exam Full Solution FRQ#2c

2013 AP Calculus AB Free Response #5

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsIntegral CalculusVolume CalculationParabola VisualizationCross SectionDefinite IntegralProblem SolvingEducational ContentMath TutorialGeometry