AP CALCULUS AB 2022 Exam Full Solution FRQ#2c

Weily Lin
20 Apr 202303:16
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a mathematical problem involving the calculation of the volume of a solid with a base enclosed by the graphs of two functions, f(x) and g(x). The cross-sections of the solid, taken perpendicular to the x-axis, are squares. The script explains the process of finding the volume by first determining the area of the cross-sectional piece, which is the difference between the logarithmic function, log(x) + 3, and the polynomial function, x^4 + 2x^3. The edge length of the square is then calculated, and its area is found by squaring this length. The thickness of each cross-sectional piece is represented by dx along the x-axis. The total volume of the solid is obtained by integrating the area of the cross-sectional pieces from x = -2 to x = 0.774. The final volume, calculated using a calculator, is approximately 5.340 cubic units, providing a clear and concise solution to the problem.

Takeaways
  • 📐 The solid's base is enclosed by the graphs of functions f and g.
  • 🟢 Cross sections of the solid perpendicular to the x-axis are squares.
  • 📏 The length perpendicular to the x-axis, h(x), determines the edge length of the square cross sections.
  • 🧮 The volume of the solid is found by calculating the area of the cross-sectional piece and multiplying by the thickness (dx).
  • 📈 The cross-sectional area is the difference between the logarithmic function log(x) + 3 and the polynomial function x^4 + 2x^3.
  • 🔵 Color coding is used to distinguish between the logarithmic graph and the polynomial function in the calculation.
  • 🛠️ The edge length of the square is obtained by taking the difference of the two functions and squaring it.
  • ∫ The total volume is calculated by integrating the area of the cross-sectional piece from x = -2 to x = 0.774.
  • 🔢 A calculator is used to perform the integration and find the volume, which results in 5.340 cubic units.
  • 📋 The process involves no complex algebraic expansion, keeping the calculation straightforward.
  • 🚫 The script emphasizes avoiding unnecessary algebraic manipulation and using a calculator for the integral.
Q & A

  • What is the shape of the base of the solid described in the transcript?

    -The base of the solid is enclosed by the graphs of two functions, f and g.

  • What are the cross sections of the solid perpendicular to the x-axis?

    -The cross sections of the solid perpendicular to the x-axis are squares.

  • How is the edge length of the square cross section determined?

    -The edge length of the square cross section is determined by the difference between the function log(x) + 3 and the polynomial function x^4 + 2x^3.

  • What is the role of 'h of X' in the calculation?

    -The 'h of X' represents the length perpendicular to the x-axis, which is used to calculate the edge length of the square cross section.

  • What is the formula used to calculate the volume of the solid?

    -The volume of the solid is calculated by taking the area of the cross-sectional piece and multiplying it by the thickness along the x-axis (represented as DX).

  • What is the method used to find the total volume of the solid?

    -The total volume of the solid is found by summing up the volume of each cross-sectional piece from the negative 2 to positive 0.774 along the x-axis.

  • What is the significance of integrating the cross-sectional area from negative 2 to 0.774?

    -Integration is used to calculate the total volume by summing up an infinite number of infinitesimally small cross-sectional areas along the x-axis within the given limits.

  • Why is a calculator used in this context?

    -A calculator is used to simplify the complex algebra involved in expanding and integrating the functions to find the volume of the solid.

  • What is the final calculated volume of the solid?

    -The final calculated volume of the solid is 5.340 cubic units.

  • What is the significance of the color coding in the transcript?

    -The color coding in the transcript is used to visually differentiate between the two functions (log graph and polynomial function) that contribute to the cross-sectional area calculation.

  • Why is it important to square the edge length of the square cross section?

    -Squaring the edge length is necessary to find the area of the square cross section, which is then used to calculate the volume of the solid.

  • What does the term 'thickness' refer to in the context of calculating the volume of the solid?

    -In the context of the solid's volume calculation, 'thickness' refers to the distance along the x-axis (DX) between each cross-sectional slice.

Outlines
00:00
📏 Calculating Solid Volume with Cross-Sections

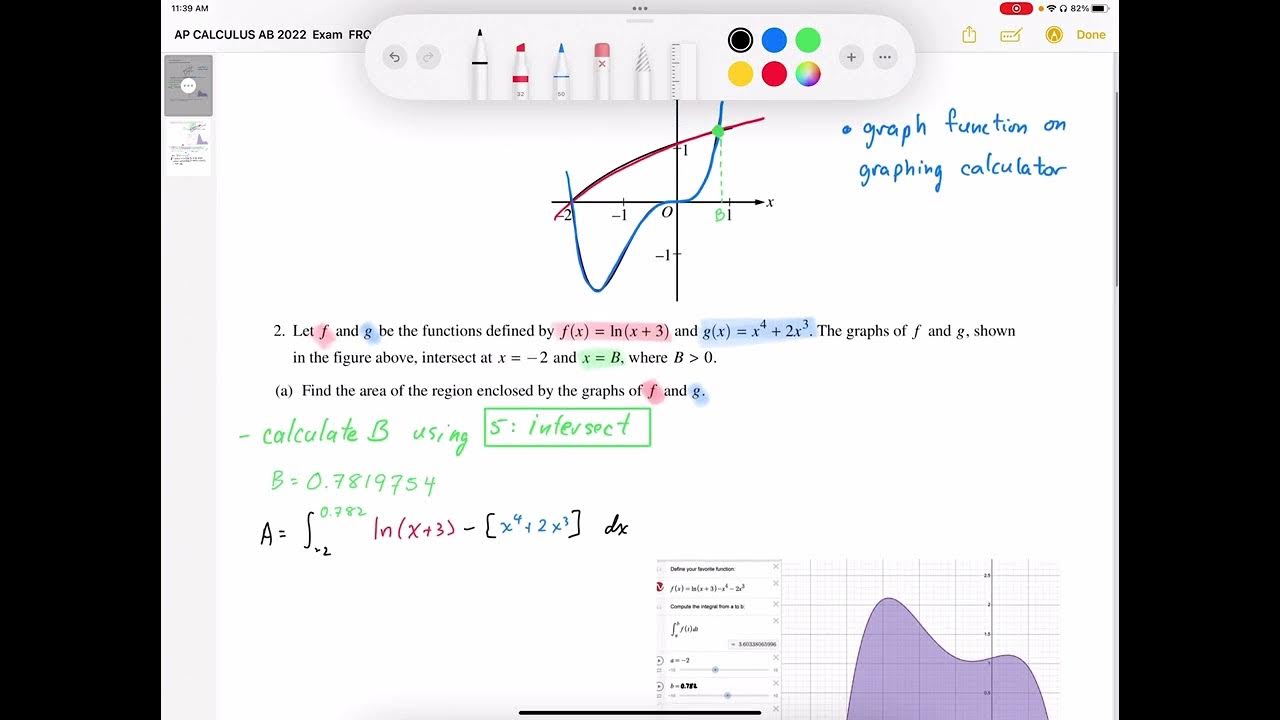
The paragraph explains the process of finding the volume of a solid with a base enclosed by the graphs of functions f and g. The cross-sections perpendicular to the x-axis are squares, and the length perpendicular to the x-axis (h of X) determines the edge length of these squares. The volume is calculated by integrating the area of the cross-sectional piece (the difference between log X plus 3 and the polynomial function X^4 plus 2X^3) over the thickness along the x-axis from -2 to 0.774. The final volume is obtained by summing these areas, resulting in a volume of 5.340 cubic units.

Mindmap
Keywords
💡Solid of Revolution
A solid of revolution is a three-dimensional object created by revolving a two-dimensional shape around an axis. In the video, the solid is formed by revolving the area between two functions around the x-axis, which is a common method in calculus to find volumes of complex shapes. The theme revolves around calculating the volume of this solid.
💡Cross Section
A cross section is a cut through an object that reveals its internal structure. In the context of the video, the cross sections are perpendicular to the x-axis and are squares, which are used to calculate the volume of the solid by integrating over the x-axis.
💡Volume Calculation
Volume calculation is the process of determining the amount of space occupied by an object. The video focuses on calculating the volume of a solid formed by revolving a region around the x-axis using the method of integration.
💡Integration
Integration is a mathematical technique used to find the accumulated sum of a function over an interval. In the video, integration is used to sum up the areas of the cross sections along the x-axis to find the total volume of the solid.
💡Logarithmic Function
A logarithmic function is a mathematical function that is the inverse of an exponential function. In the video, the logarithmic function log(x) + 3 is one of the two functions whose area difference, when revolved around the x-axis, forms the solid.
💡Polynomial Function
A polynomial function is an expression involving a sum of powers in a single variable. The video mentions a polynomial function x^4 + 2x^3, which is part of the area that, when subtracted from the logarithmic function and integrated, helps in determining the volume of the solid.
💡Area Under a Curve
The area under a curve, also known as the definite integral, represents the accumulated sum of the function values over a specified interval. The video involves finding the area between the logarithmic and polynomial functions to determine the edge length of the squares that form the solid's cross sections.
💡Edge Length
Edge length refers to the length of a side of a geometric shape, such as a square. In the video, the difference between the logarithmic and polynomial functions gives the edge length of the squares that are used to calculate the volume of the solid.
💡Thickness
In the context of the solid's volume calculation, thickness refers to the distance along the x-axis between cross sections. The video uses dx to represent an infinitesimally small thickness, which is integrated over to find the volume.
💡Definite Integral
A definite integral is a mathematical concept that calculates the exact value of an integral between two points. The video involves calculating the definite integral from negative 2 to 0.774 to find the volume of the solid.
💡Calculator
A calculator is a device used to perform mathematical operations. In the video, a calculator is used to simplify the process of finding the volume by evaluating the definite integral without manually expanding or simplifying the algebraic expression.
Highlights

The solid's base is enclosed by the graphs of functions f and g.

The cross sections of the solid taken perpendicular to the x-axis are squares.

The length perpendicular to the x-axis is calculated as h(x).

The edge length of the square cross section is determined by the difference between the log graph (log x + 3) and the polynomial function (x^4 + 2x^3).

The volume of the solid is found by multiplying the cross-sectional area by the thickness (dx) along the x-axis.

The cross-sectional area is the square of the edge length, which is the difference between the two functions.

The total volume is obtained by summing (integrating) the volumes of the cross-sectional pieces from x = -2 to x = 0.774.

The integration is performed using a calculator to avoid expanding and simplifying the algebraic expression.

The area under the curve, representing the volume of the solid, is calculated to be 5.340 units squared.

The final volume of the solid is 5.340 cubic units, obtained by multiplying the area by the thickness (dx).

The solid is generated by stacking the square cross sections vertically along the x-axis.

The problem involves finding the volume of a 3D solid with a specific base and cross-sectional shape.

The base of the solid is defined by the intersection of two functions, f and g.

The cross sections are squares perpendicular to the x-axis, with the edge length determined by the difference between two functions.

The volume is calculated using the formula for volume of a solid of revolution: cross-sectional area times thickness.

The cross-sectional area is found by squaring the difference between the two functions that define the edge length.

The integration is performed from x = -2 to x = 0.774 to find the total volume.

A calculator is used to evaluate the integral and obtain the volume of the solid.

The resulting volume of the solid is 5.340 cubic units, demonstrating the application of calculus in finding volumes of complex shapes.

Transcripts

Browse More Related Video

2022 AP Calculus AB Exam FRQ #2

2022 AP Calculus AB Free Response #2

AP CALCULUS AB 2022 Exam Full Solution FRQ#2a

Volume with cross sections: squares and rectangles (no graph) | AP Calculus AB | Khan Academy

2013 AP Calculus AB Free Response #5

Volume with cross sections: intro | Applications of integration | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsVolume CalculationIntegrationGraph AnalysisSolid GeometryCross-Sectional AreaLogarithmic FunctionPolynomial FunctionCalculusProblem SolvingEducational Content