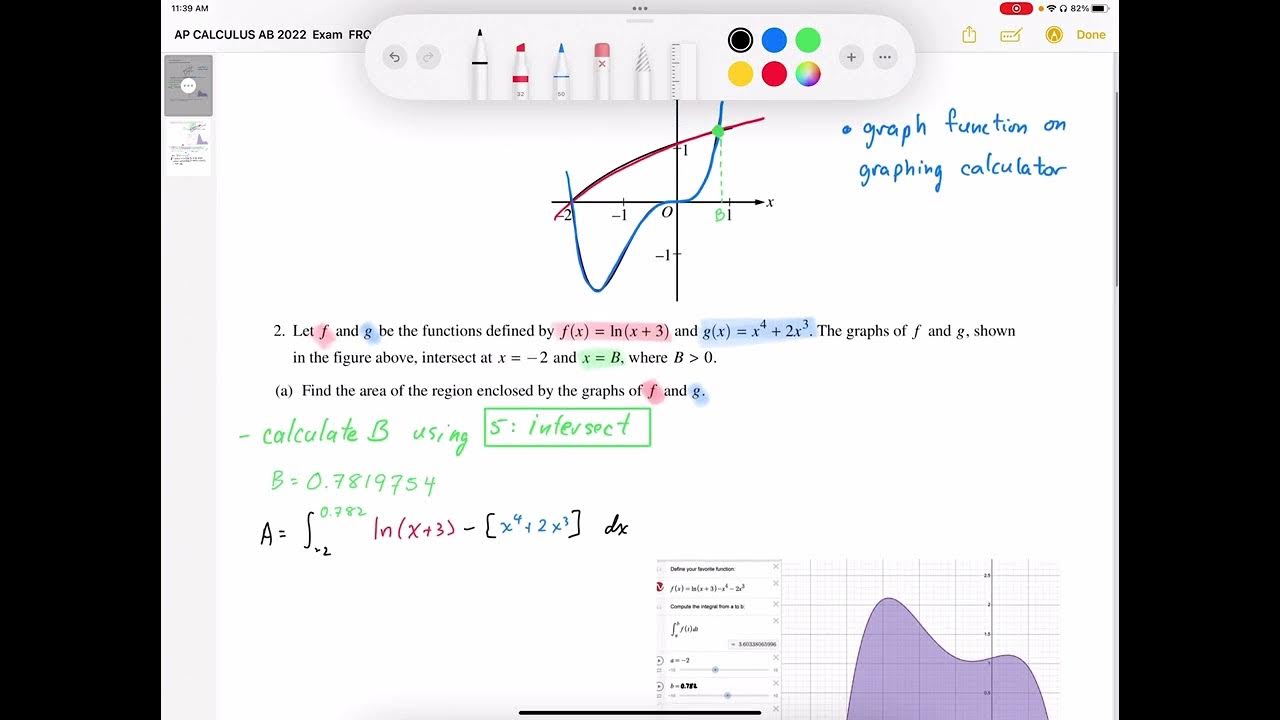
Optimization with Calculus 3
TLDRThe video script presents an intriguing optimization problem involving cutting a 100 cm wire into two pieces to form a square and an equilateral triangle. The goal is to determine the length at which to cut the wire to minimize or maximize the sum of the areas of the two shapes. Through a step-by-step geometric and calculus analysis, it is concluded that cutting the wire at approximately 56.5 cm results in a minimum combined area, while using the entire wire for the square (a = 0) yields a maximum combined area of 625 square centimeters.
Takeaways
- 📏 The problem involves cutting a 100 cm wire into two pieces to form a square and an equilateral triangle.
- 🔍 The objective is to determine where to cut the wire to minimize or maximize the sum of the areas of the two shapes formed.
- 📐 The length of the wire (100 cm) can be considered in any unit, as the problem is essentially about proportions.
- 🔢 The variable 'a' represents the length of the wire used to form the equilateral triangle, and 'b' (100 - a) for the square.
- 📊 The area of the equilateral triangle is calculated using the formula involving the square root of 3 and the side length (a/3).
- 🏢 The area of the square is derived from the side length (25 - a/4), with the formula being a quadratic equation in terms of 'a'.
- 🌟 The combined area function is the sum of the areas of the square and the triangle, expressed as a function of 'a'.
- 📈 Optimization is performed by taking the derivative of the combined area function with respect to 'a' and setting it to zero to find critical points.
- 🔄 The second derivative test is used to determine whether the critical point found is a minimum or maximum, revealing that the function is concave upwards.
- 🏆 The minimum combined area is achieved when 'a' is approximately 56.5 cm, allocating this length to the equilateral triangle and the remainder to the square.
- 🥇 The maximum combined area is obtained when 'a' is 0 cm, using the entire wire to form a square, resulting in an area of 625 square cm.
Q & A
What is the main optimization problem discussed in the transcript?
-The main optimization problem discussed is determining where to cut a 100 cm wire into two pieces, one to form a square and the other an equilateral triangle, in such a way that the sum of the areas of the two shapes is either minimized or maximized.
How is the wire initially described in the problem?
-The wire is initially described as being 100 centimeters long and is to be cut into two pieces, with one piece forming a square and the other an equilateral triangle.
What are the variables used to represent the lengths of the wire pieces?
-The variables used to represent the lengths of the wire pieces are 'a' for the piece forming the equilateral triangle and 'b' (later corrected to '100 - a') for the piece forming the square.
What is the formula derived for the area of the equilateral triangle in the transcript?
-The area of the equilateral triangle is derived to be (sqrt(3)/36) * a^2, where 'a' is the length of the wire piece used to form the triangle.
What is the formula for the area of the square formed from the wire?
-The area of the square is calculated as (625 - (50/4)*a + (a^2/16)), where 'a' represents the remaining length of the wire after the triangle is formed.
How is the combined area function expressed in terms of 'a'?
-The combined area function is expressed as the sum of the areas of the equilateral triangle and the square, which is (sqrt(3)/36) * a^2 + (625 - (50/4)*a + (a^2/16)).
What method is used to find the minimum and maximum values of the combined area function?
-Calculus is used to find the minimum and maximum values of the combined area function, specifically by taking the first derivative of the function, setting it to zero to find critical points, and then taking the second derivative to determine whether these points are minima or maxima.
What is the result of the optimization problem when minimizing the combined area?
-The result of the optimization problem when minimizing the combined area is at a = 56.5 cm, where the wire is cut to form an equilateral triangle with 56.5 cm and a square with the remaining 43.5 cm.
What is the maximum combined area according to the transcript?
-The maximum combined area is 625 square centimeters, which occurs when the entire 100 cm wire is used to form a square, with no wire left for the triangle.
How does the second derivative test confirm that a = 56.5 cm is a minimum point?
-The second derivative test confirms that a = 56.5 cm is a minimum point because the second derivative of the combined area function with respect to 'a' is a positive constant, indicating that the function is concave upwards and thus the slope is increasing at this point, which is characteristic of a minimum.
What are the boundary conditions considered for maximizing the combined area?
-The boundary conditions considered for maximizing the combined area are when 'a' is 0 (using the entire wire for the square) and when 'a' is 100 (using the entire wire for the triangle).
What is the conclusion of the optimization problem?
-The conclusion is that the minimum combined area is achieved by cutting the wire at 56.5 cm for the triangle and 43.5 cm for the square, while the maximum combined area is achieved by using the entire wire for the square, resulting in an area of 625 square centimeters.
Outlines
📏 Introduction to the Optimization Problem
The speaker introduces an optimization problem involving a 100 cm wire cut into two pieces, one forming a square and the other an equilateral triangle. The goal is to find the cut length 'a' that minimizes or maximizes the sum of the areas of the two shapes. The problem allows for the possibility of no cut, meaning the entire wire could form either a square or a triangle. The speaker begins to visualize the problem and sets up the initial conditions, using 'a' for the length of the wire segment forming the triangle and '100 - a' for the segment forming the square.
📐 Calculating the Areas and Setting Up the Equation
The speaker delves into the geometry behind the problem, explaining how to calculate the areas of the equilateral triangle and the square formed from the wire segments. The area of the triangle is derived using the formula involving the square root of 3 and the side length 'a'. The area of the square is calculated using the side length '25 - a/4'. The combined area 'A_combined' is then expressed as a function of 'a', summing the areas of both shapes. The speaker sets up the calculus for optimization by finding the derivative of the combined area function with respect to 'a'.
🔢 Solving for the Optimal Cut Length 'a'
The speaker solves for the optimal cut length 'a' by setting the derivative of the combined area function equal to zero and solving the resulting equation. After simplifying the equation, the speaker finds that 'a' is approximately 56.5 cm. The speaker then discusses the implications of this value, noting that it falls within the valid range of 0 to 100 cm. The speaker questions whether this value represents a minimum or maximum and decides to investigate further by considering the concavity of the function at this point.
📈 Determining the Nature of the Extremum and Maximizing the Combined Area
The speaker analyzes the second derivative of the combined area function to determine the nature of the extremum found at 'a' = 56.5 cm, concluding that it is a minimum point due to the function being concave upwards. The speaker then explores the boundary conditions by setting 'a' to 0 and 100 to find the maximum combined area. At 'a' = 0, the entire wire forms a square with an area of 625 cm², and at 'a' = 100, the entire wire forms a triangle with an area of 481 cm². The speaker concludes that the maximum combined area is achieved when 'a' is 0, resulting in a square with an area of 625 cm², and the minimum combined area is achieved at 'a' ≈ 56.5, allocating 56.5 cm to the triangle and 43.5 cm to the square.
Mindmap
Keywords
💡Optimization Problem
💡Centimeters
💡Equilateral Triangle
💡Square
💡Area
💡Perimeter
💡Calculus
💡Derivative
💡Second Derivative
💡Boundary Conditions
💡Minimum and Maximum
Highlights
The optimization problem involves cutting a 100 cm wire into two pieces to form a square and an equilateral triangle.
The goal is to find the cut length 'a' that minimizes or maximizes the sum of the areas of the square and the triangle.
The wire is cut at a point 'a' centimeters from the left-hand side, with the remaining length being 100 - a centimeters.
The side length of the equilateral triangle formed from length 'a' is a/3.
The side length of the square formed from the remaining length (100 - a) is (25 - a/4).
The area of the equilateral triangle is calculated using the formula (sqrt(3)/36) * a^2.
The area of the square is calculated using the formula (625 - 50/4a + a^2/16).
The combined area function is the sum of the areas of the square and the triangle.
To find the minimum or maximum, the derivative of the combined area function with respect to 'a' is set to zero.
The first derivative of the combined area function is (a/8 - 50/4) + (2/sqrt(3)/18)a.
The second derivative of the combined area function is a positive constant, indicating the function is concave upwards.
The minimum combined area is achieved when 'a' is approximately 56.5 cm, committing 56.5 to the triangle and 43.5 to the square.
The maximum combined area is 625 square centimeters, achieved by using the entire 100 cm wire to form a square.
The problem-solving approach combines geometric understanding with calculus for optimization.
The problem is solved without the use of complex software or tools, relying on manual calculations and logical reasoning.
The process demonstrates the practical application of mathematical concepts in solving real-world problems.
The problem highlights the importance of precision and attention to detail in mathematical calculations.
The solution involves a step-by-step explanation, making it accessible for various levels of mathematical understanding.
The problem provides an example of how to apply mathematical optimization to geometric shapes.
The conclusion of the problem emphasizes the value of both minimum and maximum solutions in practical scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: