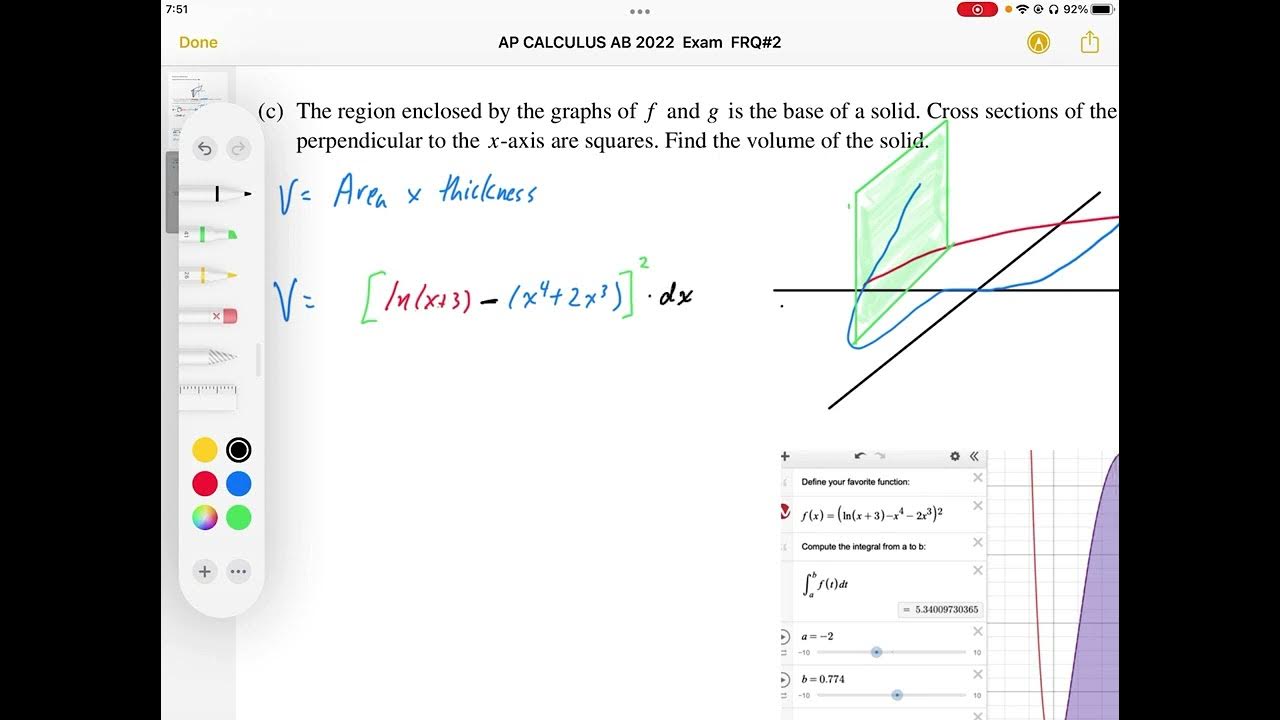
AP CALCULUS AB 2022 Exam Full Solution FRQ#2a
TLDRThe video script discusses a graphing calculator problem involving two functions: a logarithmic function f(x) = log(x) + 3 and a polynomial function g(x) = x^4 + 2x^3. The problem requires finding the area enclosed by the graphs of these functions, which intersect at x = -2 and an unknown point B. Using a graphing calculator, the intersection point B is determined to be approximately 0.7819. The area under the curves is calculated by integrating the difference between the two functions from x = -2 to x = 0.7819. Two methods are demonstrated: one by integrating the combined function and the other by finding the area under the logarithmic function and subtracting the area under the polynomial function. The graphing calculator yields an area of approximately 3.604 square units, confirming the correct calculation of the enclosed region.
Takeaways
- 📊 The problem involves graphing and finding the area between two functions, f(x) and g(x), represented by a logarithmic function and a polynomial function respectively.
- 🔍 The logarithmic function is defined as f(x) = log(x) + 3, and the polynomial function is g(x) = x^4 + 2x^3.
- 🤔 The graphs of these functions intersect at x = -2 and at an unknown point x = B.
- 🔢 To find the value of B, the script uses a graphing calculator and the intersect function (calc 5) on a TI-84 calculator, resulting in B ≈ 0.7819754.
- 📐 The area to be found is between the two curves from the lower bound x = -2 to the upper bound x = 0.782.
- 📈 The integration method involves subtracting the polynomial function from the logarithmic function to find the area under the curves.
- ∫ The integral to calculate the area is taken from -2 to 0.782 of (log(x) + 3) - (x^4 + 2x^3) dx.
- 📊 The graphing calculator is used to visualize and integrate the functions, providing a graphical representation of the area to be calculated.
- 📝 The area calculated using the graphing calculator is approximately 3.604 square units.
- 🤓 An alternative method is mentioned where the area under the log function is found and then the area under the polynomial function is subtracted.
- 📐 The alternative method yields the same result of 3.604 square units for the enclosed area.
- 📚 The process demonstrates the use of a graphing calculator for solving complex integration problems and finding areas between curves.
Q & A
What is the problem with the graphing calculator that the transcript discusses?
-The problem involves finding the area enclosed by the graphs of two functions, f(x) = log(x) + 3 and g(x) = x^4 + 2x^3, which intersect at x = -2 and an unknown point B.
What are the two functions given in the problem?
-The two functions given are f(x) = log(x) + 3 (represented in red) and g(x) = x^4 + 2x^3 (represented in blue).
How does one find the value of B where the two graphs intersect?
-To find the value of B, one needs to use the intersect function (calc 5) on a graphing calculator like the TI-84, which yields B ≈ 0.7819.
What are the bounds of integration for calculating the area between the curves?
-The bounds of integration are from x = -2 to x = 0.7819, as these are the points where the two functions intersect.
How does one calculate the area under the curves?
-The area is calculated by integrating the upper function f(x) minus the lower function g(x) from the lower bound to the upper bound.
What is the result of the integration on the graphing calculator?
-The area enclosed by the graphs of f and g, as calculated by the graphing calculator, is approximately 3.604 square units.
What is an alternative method to find the area under the curves?
-An alternative method is to find the area under the log function from x = -2 to x = 0.7819 and then subtract the area under the polynomial function with the same bounds.
What is the area under the log function from x = -2 to x = 0.7819?
-The area under the log function from x = -2 to x = 0.7819 is approximately 2.249.
What is the area under the polynomial function from x = -2 to x = 0.7819?
-The area under the polynomial function from x = -2 to x = 0.7819 is a negative area, approximately -1.355 am (which seems to be a unit error or typo in the transcript).
How does the negative area under the polynomial function affect the final area calculation?
-The negative area under the polynomial function is subtracted from the area under the log function, resulting in the final positive area of 3.604 square units.
What is the significance of the negative area in the polynomial function's calculation?
-The negative area indicates that part of the polynomial function lies below the x-axis, and its contribution to the total area is subtractive rather than additive.
What tool is used to perform the integration on the graphing calculator?
-The integrate function (under calc and then 7) on the graphing calculator is used to perform the integration.
Outlines
📈 Graphing Calculator Problem: Finding Enclosed Area
The paragraph introduces a graphing calculator problem involving the intersection of two functions: a logarithmic function f(x) = log(x) + 3 and a polynomial function g(x) = x^4 + 2x^3. The graphs of these functions intersect at x = -2 and an unknown point B. The task is to find the area enclosed by the graphs. To solve this, one must first graph the functions and find the intersection point B using the intersect function on a TI-84 calculator. The value of B is determined to be approximately 0.7819. With the bounds known, the area is calculated by integrating the difference between the upper function (logarithmic) and the lower function (polynomial) from x = -2 to x = 0.782. The integration yields an area of approximately 3.604 square units. An alternative method is also mentioned, which involves calculating the area under the logarithmic function and subtracting the area under the polynomial function within the same bounds, leading to the same result.
Mindmap
Keywords
💡Graphing Calculator
💡Log Function
💡Polynomial Function
💡Intersection
💡Integration
💡CALC Function
💡Bounds of Integration
💡Area Calculation
💡Integration Function
💡Units Squared
💡TI-84 Calculator
Highlights
The problem involves graphing two functions, f(x) = log(x) + 3 and g(x) = x^4 + 2x^3, and finding the area enclosed by their graphs.
The graphs intersect at x = -2 and an unknown point B.
To find the intersection point B, use the intersect function (calc 5) on a graphing calculator like the TI-84.
The value of B is calculated to be approximately 0.7821754.
The bounds of integration for finding the area are from x = -2 to x = B.
The area can be calculated by integrating the difference of the two functions: f(x) - g(x).
The upper function to integrate is log(x) + 3 and the lower function is x^4 + 2x^3.
The integral is evaluated from the lower bound of -2 to the upper bound of 0.782.
Using the integrate function (calc 7) on the graphing calculator, the area is found to be approximately 3.604 square units.
Alternatively, the area under the log function from -2 to 0.782 can be found first, which is approximately 2.249.
Then the area under the polynomial function from -2 to 0.782, which is approximately -1.355, can be subtracted to get the final area of 3.604.
The problem demonstrates the application of graphing calculators in solving area problems involving functions.
The intersect function (calc 5) is a key tool for finding points of intersection between two functions.
The area between two curves can be found by integrating the difference of the functions over a given interval.
The integrate function (calc 7) on a graphing calculator can be used to evaluate the area numerically.
Combining the functions f(x) - g(x) allows for calculating the area in one step, rather than finding the areas under each function separately.
The problem involves using logarithmic and polynomial functions, which are fundamental concepts in calculus.
The solution process is explained step-by-step, making it accessible to learners with some background in calculus.
The problem illustrates the practical application of calculus in finding areas enclosed by curves.
Using a graphing calculator simplifies the process of finding intersections and evaluating integrals.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: