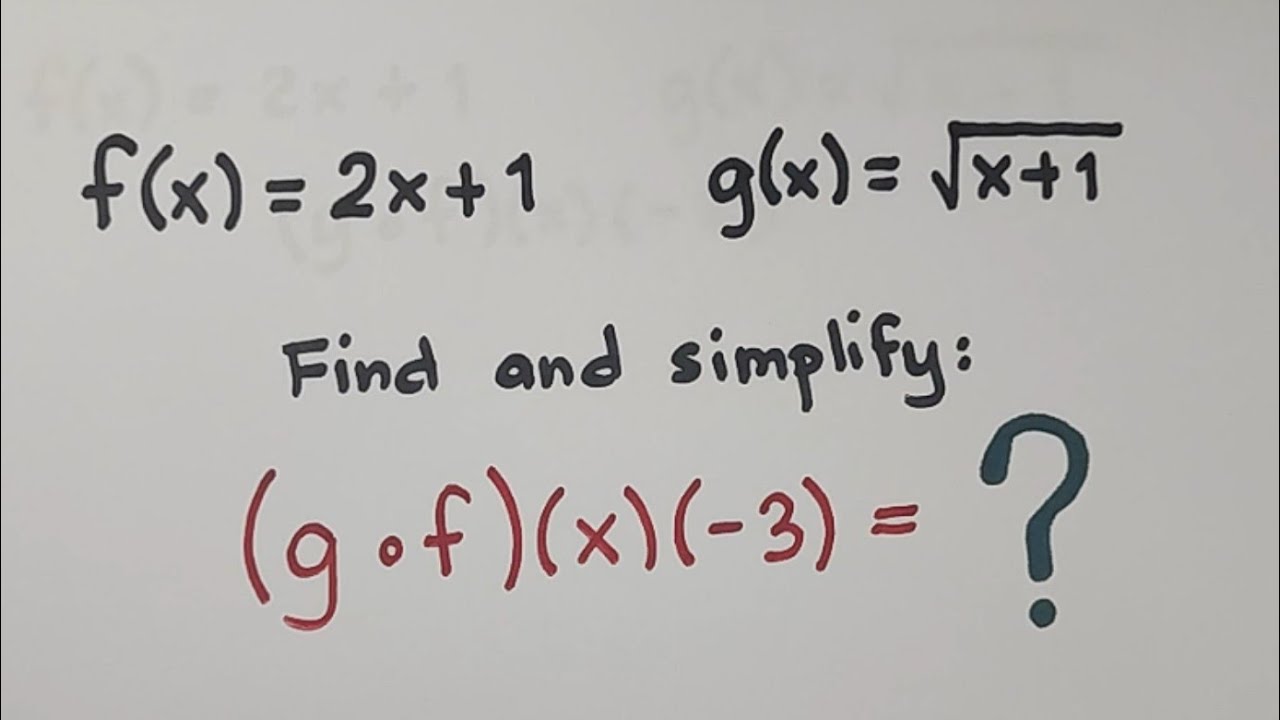Composite Functions
TLDRThis video tutorial provides a clear guide on evaluating composite functions, using two detailed examples to demonstrate the process. The first example involves the functions g(x) = 2x - 3 and f(x) = x - 1, leading to the evaluation of g(f(x)) and f(g(x)). The second example features functions f(x) = (2x + 4)/5 and g(x) = 3x - 7, with an additional application involving the specific value of x = 5. The video concludes with a challenge for viewers to apply the concepts learned.
Takeaways
- 📚 The video discusses the process of evaluating composite functions, which are functions where one function is nested inside another.
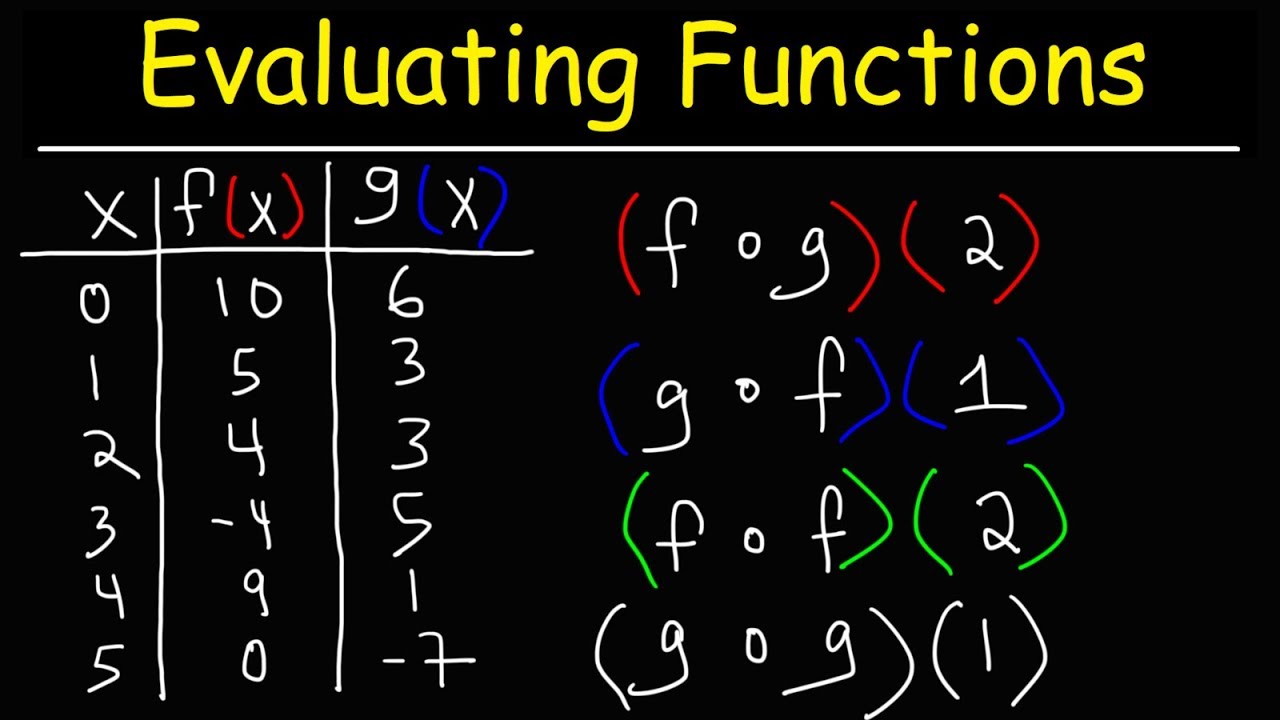
- 🔍 The first example given involves the functions g(x) = 2x - 3 and f(x) = x - 1, and the task is to find g(f(x)) and f(g(x)).
- 🧠 To evaluate g(f(x)), the f(x) function is substituted into the g(x) function, replacing every instance of x with (x - 1).
- 📈 After substitution and simplification, g(f(x)) is found to be 2x - 5.
- 🔄 Similarly, to find f(g(x)), the g(x) function is substituted into the f(x) function, replacing x with (2x - 3).
- 📊 After performing the substitution and simplifying, f(g(x)) is calculated to be 2x - 4.
- 📝 The second example involves the functions f(x) = (2x + 4) / 5 and g(x) = 3x - 7, with the goal to find f(g(x)) and evaluate f(g(5)).
- 👉 For the second example, f(g(x)) is determined by substituting g(x) into f(x), resulting in a function (6x - 10) / 5.
- 🏁 Evaluating f(g(5)) involves substituting x with 5 in the f(g(x)) function, yielding a result of 4.
- 💡 The video emphasizes the importance of understanding substitution and simplification in evaluating composite functions.
- 🎓 The video concludes with a challenge for viewers to evaluate a composite function on their own and engage with the content by sharing their answers in the comments.
- 🔔 The channel encourages viewers to subscribe, like the video, and turn on notifications for new content updates.
Q & A
What is the main topic of the video?
-The main topic of the video is how to evaluate composite functions.
What are the two functions given in example one?
-In example one, the functions given are g(x) = 2x - 3 and f(x) = x - 1.
What is the first part of the evaluation in example one?
-The first part of the evaluation in example one is to find g(f(x)).
How is g(f(x)) evaluated in the video?
-g(f(x)) is evaluated by substituting f(x) into g(x), which results in 2(x - 1) - 3, simplifying to 2x - 5.
What is the second part of the evaluation in example one?
-The second part of the evaluation in example one is to find f(g(x)).
How is f(g(x)) evaluated in the video?
-f(g(x)) is evaluated by substituting g(x) into f(x), which results in (2x - 3) - 1, simplifying to 2x - 4.
What are the functions given in example two?
-In example two, the functions given are f(x) = (2x + 4)/5 and g(x) = 3x - 7.
What is the first part of the evaluation in example two?
-The first part of the evaluation in example two is to find f(g(x)).
How is f(g(x)) evaluated in example two?
-f(g(x)) is evaluated by substituting g(x) into f(x), which results in (2(3x - 7) + 4)/5, simplifying to (6x - 10)/5.
What is the second part of the evaluation in example two?
-The second part of the evaluation in example two is to determine f(g(5)).
How is f(g(5)) evaluated in the video?
-f(g(5)) is evaluated by substituting x with 5 in the f(g(x)) expression, resulting in 4.
What is the final result of f(g(5)) in example two?
-The final result of f(g(5)) in example two is 4.
What does the video encourage viewers to do at the end?
-The video encourages viewers to evaluate a question presented on screen and share their answers in the comments, as well as to subscribe to the channel, like the video, and turn on notifications.
Outlines
📚 Evaluating Composite Functions - Part 1
This paragraph introduces the topic of evaluating composite functions and sets the stage for the examples to follow. The video aims to explain the process of substitution and simplification involved in evaluating composite functions, starting with an example where g(x) = 2x - 3 and f(x) = x - 1. The first part of the example focuses on finding g(f(x)) by substituting the f(x) function into the g(x) function, leading to the result g(f(x)) = 2x - 5. The explanation is detailed, walking through each step of the substitution and simplification process.
📝 Further Exploration of Composite Functions - Part 2
The second paragraph continues the exploration of composite functions with a new set of functions, f(x) = (2x + 4)/5 and g(x) = 3x - 7. The task here is to find f(g(x)) and then evaluate f(g(5)). The explanation emphasizes the method of substitution, where the g(x) function is inserted into the f(x) function, resulting in f(g(x)) = (6x - 10)/5. The paragraph concludes with the specific evaluation of f(g(5)), which simplifies to 4. The paragraph also includes a prompt for viewers to engage with the content by evaluating a screen-displayed question and sharing their answers in the comments.
Mindmap
Keywords
💡Composite Functions
💡Function Evaluation
💡Substitution
💡Distributive Law
💡Simplification
💡Algebra
💡Functions
💡Mathematical Expressions
💡Like and Subscribe
💡Notification Bell
💡Examples
Highlights
The video discusses the process of evaluating composite functions, providing a clear and detailed explanation.
The presenter introduces two examples to illustrate the evaluation of composite functions.
In the first example, the functions given are g(x) = 2x - 3 and f(x) = x - 1.
To find g(f(x)), the f(x) function is substituted into the g(x) function.
The result of g(f(x)) is 2x - 5, derived by applying the distributive law and simplifying the expression.
For the second part of the example, f(g(x)) is found by substituting g(x) into f(x).
The final expression for f(g(x)) is 2x - 4, obtained by replacing x with (2x - 3) in the f(x) function.
The second example involves functions f(x) = (2x + 4)/5 and g(x) = 3x - 7.
To find f(g(x)), the g(x) function is substituted into the f(x) function, resulting in an expression (2(3x - 7) + 4)/5.
Simplifying the expression for f(g(x)) yields 6x - 10/5, or 6x - 2.
The video then demonstrates how to find the specific value of f(g(5)) by substituting x with 5 in the f(g(x)) expression.
The result of f(g(5)) is 4, showing the practical application of composite function evaluation.
The presenter emphasizes the importance of understanding the order of operations and substitution in composite functions.
The video concludes with a challenge question for viewers to practice their understanding of composite functions.
The presenter encourages viewers to engage with the content by subscribing to the channel and participating in the comments section.
The video provides a comprehensive guide to evaluating composite functions, suitable for learners at various levels.
The use of step-by-step examples helps to clarify the process of substitution and simplification in composite functions.
The video's approach to teaching composite functions is both practical and accessible, making it an excellent resource for educational purposes.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: