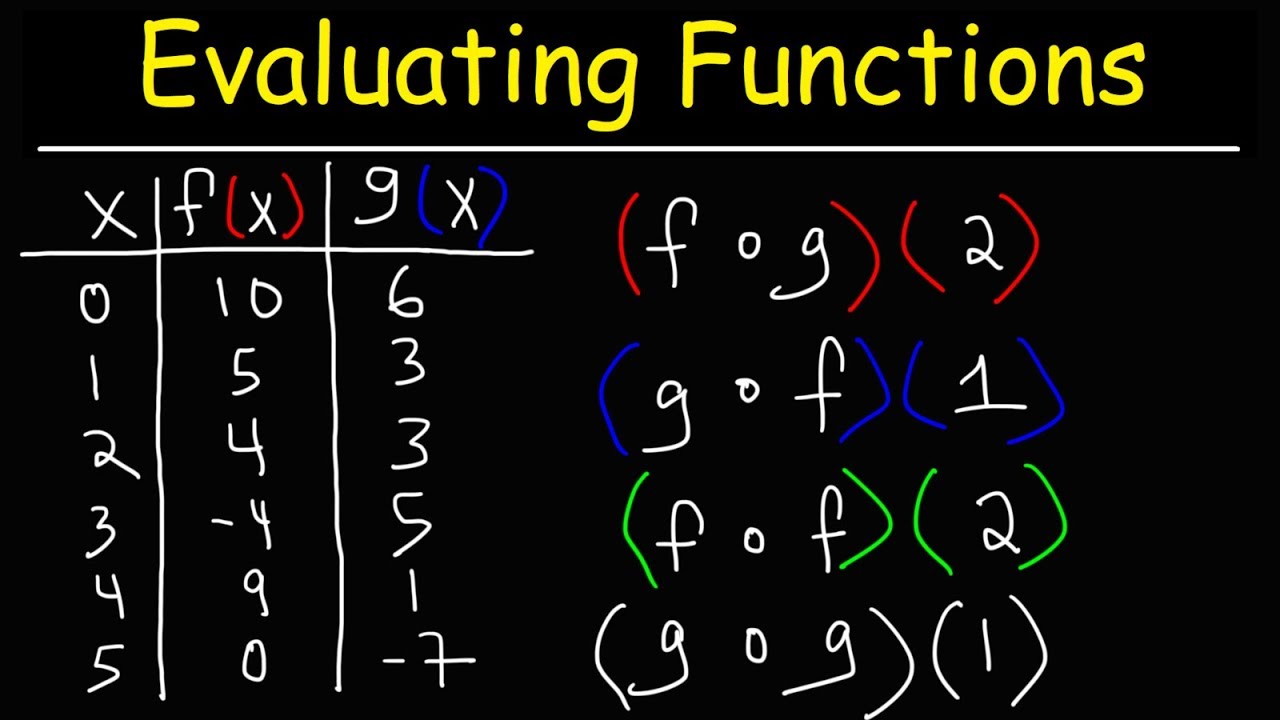
Composition of Function - General Mathematics - Grade 11

MATH TEACHER GON
3 Sept 202209:20
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the teacher explains the concept of composite functions with clarity. The focus is on evaluating a specific composite function, g(f(x)), where f(x) = x + 1 and g(x) = √(x) + 1, at x = -3. The step-by-step process involves first evaluating g(f(x)) and then substituting x with -3, leading to the conclusion of an imaginary number result, 2i. The video also touches on evaluating another composite function with a different set of functions, demonstrating the versatility of the method. The teacher encourages engagement with the content and the channel, promoting further learning and interaction.

Takeaways
  • 📚 The topic of the video is about composite functions and evaluating a given composite function with specific input values.
  • 🔢 Two functions are introduced: f(x) = x + 1 and g(x) = √(x) + 1.
  • 🌟 The goal is to simplify and evaluate g(f(x)) for x = -3.
  • 🎯 First, evaluate g(f(x)) by substituting f(x) into g(x), resulting in √(2x + 1) + 1.
  • 🛠️ When x = -3, the expression becomes √(2(-3)) + 2, which simplifies to √(-6) + 2.
  • 📐 The square root of a negative number leads to an imaginary result: √(-4) = 2i.
  • 🥇 The final evaluated value of g(f(x)) when x = -3 is 2i.
  • 📝 Another example is given involving a fractional expression with f(x) = 2x + 1 and g(x) = (2x + 1) / (x - 1).
  • 🧠 The process of evaluating g(f(x)) involves simplifying the expression by substituting f(x) into g(x) and then evaluating at the given input.
  • 📊 For the second example, f(r) = 6 + 1, which simplifies to 7 when evaluated at x = 2.
  • 📌 The video emphasizes the step-by-step process of evaluating composite functions with specific input values.
Q & A

  • What is the topic of the video?

    -The topic of the video is about composite functions and evaluating a given composite function.

  • What are the two functions given in the example?

    -The two functions given are f(x) = x + 1 and g(x) = √(x) + 1.

  • What is the composite function g(f(x)) that needs to be simplified and evaluated?

    -The composite function g(f(x)) is g(x) evaluated at f(x), which becomes √(2x + 1) + 1 after substitution.

  • What is the value of the composite function g(f(x)) when x is -3?

    -When x is -3, the value of g(f(x)) is 2i, which is the square root of -4, representing an imaginary number.

  • How does the teacher guide the students through the process of evaluating g(f(x)) at x = -3?

    -The teacher first explains to evaluate g(f(x)) by substituting f(x) into g(x), then simplifies the expression, and finally evaluates it by replacing x with -3 to get the result of 2i.

  • What is the second example given in the script?

    -The second example involves the function f(r(x)) where r(x) = 2x + 1 and the task is to evaluate f(r(x)) at x = 2.

  • What is the result of the function f(r(x)) when x is 2?

    -The result of f(r(x)) when x is 2 is 7, after simplifying the expression 4x + 2 over x - 1 plus 1.

  • How does the teacher simplify the expression for the second example?

    -The teacher simplifies the expression by applying the distributive property, multiplying and dividing the terms, and then combining like terms to get the final result.

  • What advice does the teacher give on how to approach evaluating composite functions?

    -The teacher advises to first evaluate the inner function, substitute it into the outer function, simplify the resulting expression, and then evaluate it with the given input value.

  • What is the significance of the imaginary number in the context of the first example?

    -The imaginary number, represented by 'i', is significant because it shows that the square root of a negative number is not a real number but an imaginary one, which is a fundamental concept in complex number theory.

  • How does the teacher conclude the video?

    -The teacher concludes by summarizing the method of evaluating composite functions with specific input values and encourages students to follow his social media accounts for updates.

Outlines
00:00
📚 Introduction to Composite Functions

This paragraph introduces the concept of composite functions, explaining the task of evaluating a given composite function with specific values. The example provided involves two functions, f(x) = x + 1 and g(x) = √(x) + 1, and the goal is to simplify and evaluate g(f(x)) for x = -3. The explanation includes a step-by-step solution, highlighting the process of substituting values and simplifying expressions, leading to the conclusion that g(f(x)) = √(2x) + 1. The final evaluation results in an imaginary number, 2i, demonstrating the concept of complex numbers in the context of composite functions.

05:01
📝 Evaluating Composite Functions with Fractional Input

The second paragraph continues the discussion on evaluating composite functions, this time with a fractional input. The functions involved are f(x) = 2x + 1 and the composite function is evaluated for x = 2. The process involves simplifying the expression by substituting the value of x into the function and applying the distributive property. The summary walks through the arithmetic steps, leading to the final evaluation of f(x) for x = 2 as 7. The paragraph concludes by emphasizing the methodical approach to evaluating composite functions with specific inputs and encourages viewers to follow the instructor's social media accounts for updates.

Mindmap
Keywords
💡composite function
A composite function is a function that is formed by combining two or more functions in such a way that the output of one function becomes the input of another. In the video, the functions f(x) = x + 1 and g(x) = √x + 1 are used to form the composite function g(f(x)). The video demonstrates how to evaluate this composite function at a specific input value.
💡evaluate
To evaluate a function means to find its value for a specific input or argument. In the context of the video, the teacher is guiding the viewers through the process of evaluating a composite function at a given input value, such as g(f(-3)) where -3 is the input.
💡function
A function is a mathematical relation that pairs each element from a set (called the domain) with exactly one element from another set (called the range). Functions are typically represented by a symbol, such as f, followed by an argument within parentheses, like f(x). In the video, two functions, f(x) and g(x), are defined and used to create a composite function.
💡square root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the symbol √ and is used in the function g(x) = √(x) + 1 in the video. Square roots are particularly relevant when dealing with real numbers and are a fundamental concept in mathematics.
💡input
In the context of functions, the input is the value that is given to the function to obtain an output. The input is often represented by a variable, such as x, and is essential for evaluating functions and composite functions.
💡output
The output of a function is the result or value that is returned when a specific input is provided to the function. In the video, the output is the value obtained after evaluating the composite function g(f(x)) at a particular input.
💡imaginary number
An imaginary number is a number that can be written in the form of i times a real number, where i is the square root of -1. Imaginary numbers are used to extend the real number system to include numbers that do not have real square roots. In the video, the square root of -4 results in an imaginary number, 2i.
💡step-by-step solution
A step-by-step solution is a detailed, sequential process for solving a mathematical problem. It breaks down the problem into smaller, manageable steps, making it easier to understand and follow. The video provides a step-by-step approach to evaluating a composite function at a specific input.
💡simplify
To simplify a mathematical expression means to reduce it to a more straightforward form, often by applying arithmetic rules and properties. Simplification helps to make expressions easier to understand and compute. In the video, the teacher simplifies the composite function to find its value at a given input.
💡negative number
A negative number is a number that is less than zero. In the context of the video, negative numbers are used as input values for the functions, and understanding how to handle them is crucial for evaluating functions correctly.
💡domain
The domain of a function is the set of all possible input values (x-values) for which the function is defined. It is important to consider the domain when evaluating functions, especially when dealing with square roots or other operations that may not be defined for all real numbers.
Highlights

Introduction to composite functions and evaluation of a given composite function.

Two functions given: f(x) = x + 1 and g(x) = sqrt(x) + 1.

Task to simplify and find g(f(x)) for x = -3.

Explanation of the step-by-step process to evaluate g(f(x)) for a given x value.

First method to evaluate g(f(x)) involves finding g(x) first.

Substitution of x with (x + 1) in the function g to find g(f(x)).

Simplification of g(f(x)) to the square root of (2x + 1) + 1.

Evaluation of g(f(x)) for x = -3 results in the square root of (-6 + 2).

The square root of negative four results in an imaginary number, 2i.

Final evaluation of g(f(x)) for x = -3 is 2i.

Introduction of the next example involving a fractional expression.

Evaluation of f(r(x)) where r(x) = 2x + 1 and the input x is 2.

Substitution of x with (2x + 1) in the function f and simplification.

Result of f(r(x)) for x = 2 is a simplified fraction.

Further simplification leads to the final result of f(r(x)) = 7.

Explanation of how to evaluate a composite function with a specific input in a step-by-step manner.

The video provides a clear and detailed walkthrough for understanding composite functions and their evaluation.

Transcripts

Browse More Related Video

Composite Functions

How To Evaluate Composite Functions Using Function Tables | Precalculus

Composite Function Explained - The Basics You NEED To Know!

Composition of Functions (Precalculus - College Algebra 48)

Composite Functions

Composite and Inverse Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsComposite FunctionsFunction EvaluationImaginary NumbersEducational ContentMath TutorialSquare RootsAlgebraMathematics TeachingOnline Learning