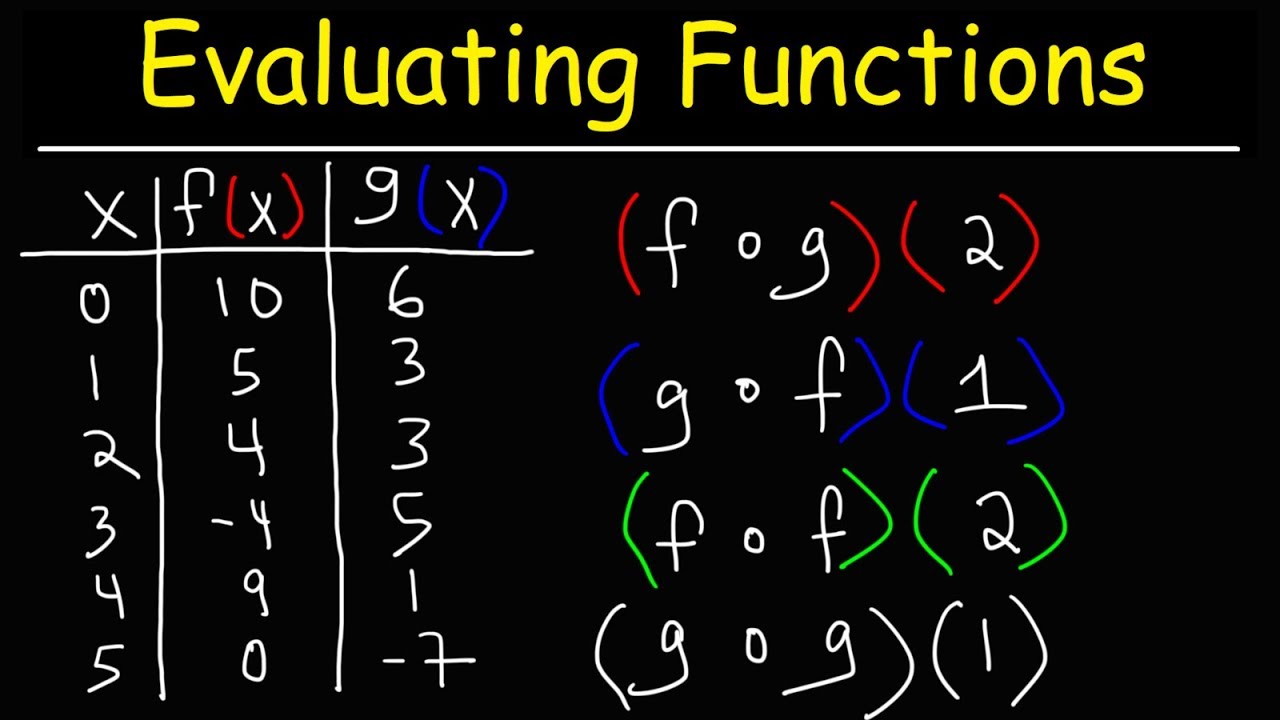
Composite Functions

The Organic Chemistry Tutor
2 Feb 201805:23
EducationalLearning
32 Likes 10 Comments

TLDRThis video lesson delves into the concept of composite functions, demonstrating how to compute f(g(x)) and g(f(x)) using given functions f(x) = 3x - 4 and g(x) = x^2 - 3. It illustrates the process of substitution and distribution to find the resulting expressions, and applies these methods to evaluate the functions at specific points, such as f(g(2)) and g(f(-1)). The lesson is a comprehensive guide to understanding and working with composite functions in mathematics.

Takeaways
  • 📚 Composite functions involve one function being 'inside' another, denoted by f(g(x)).
  • 🔢 To find f(g), replace the 'x' in the function f with the entire function g(x).
  • 📈 For f(g), the order of functions matters; f(x) * g(x) represents multiplication, not composition.
  • 🌟 Example given: f(x) = 3x - 4 and g(x) = x^2 - 3, so f(g(x)) = 3(x^2 - 3) - 4 = 3x^2 - 13.
  • 🔄 To calculate g(f), the process is reversed; replace the 'x' in g(x) with the expression of f(x).
  • 📊 Another example: f(x) = 5x + 2, g(x) = x^3 - 4, and evaluating f(g(2)) results in 5(2^3 - 4) + 2 = 22.
  • 🤔 When finding g(f), first evaluate the inner function f(x), then substitute the result into g(x).
  • 🧠 Example for g(f): f(x) = 5x + 2, g(x) = x^3 - 4, and g(f(-1)) = (5(-1) + 2)^3 - 4 = -31.
  • 📝 It's important to follow the correct order of operations when dealing with composite functions.
  • 🔍 Always distribute and simplify expressions as needed when calculating composite functions.
  • 📈 Understanding composite functions is crucial for advanced mathematical concepts and problem-solving.
  • 🎓 The ability to evaluate composite functions is a key skill in algebra and calculus.
Q & A

  • What is a composite function?

    -A composite function is when one function is inside of another, symbolized by an open circle. It is different from function multiplication.

  • How is the composite function f(g(x)) calculated given f(x) = 3x - 4 and g(x) = x^2 - 3?

    -To calculate f(g(x)), replace x in f(x) with g(x). This gives f(g(x)) = 3(x^2 - 3) - 4, which simplifies to 3x^2 - 13.

  • What mistake is made in the calculation of g(f(x)) in the transcript?

    -The mistake is in the step of squaring 3x - 4; it is incorrectly expanded as 3x - 4 times 2x - 4. The correct expansion involves squaring the entire expression (3x - 4)^2.

  • How do you correctly calculate g(f(x)) given f(x) = 3x - 4 and g(x) = x^2 - 3?

    -Correctly calculate g(f(x)) by plugging f(x) into g(x). This means replacing x in g(x) with 3x - 4, and correctly expanding (3x - 4)^2, then subtracting 3.

  • What are the correct steps to evaluate f(g(2)) given f(x) = 5x + 2 and g(x) = x^3 - 4?

    -First, find g(2), which is 2^3 - 4 = 4. Then, evaluate f(g(2)) by plugging g(2) into f(x), resulting in f(4) = 5(4) + 2 = 22.

  • How do you find the value of g(f(-1)) with the given functions f(x) = 5x + 2 and g(x) = x^3 - 4?

    -First, evaluate f(-1) = 5(-1) + 2 = -3. Then, calculate g(f(-1)) by substituting f(-1) into g(x), leading to g(-3) = (-3)^3 - 4 = -27 - 4 = -31.

  • What symbol is used to indicate multiplication between two functions, and how is it different from the symbol for composition?

    -A closed circle symbolizes function multiplication, which is different from the open circle used to indicate composition of functions.

  • How does the concept of function composition differ from the traditional algebraic operations?

    -Function composition involves inserting one function into another, rather than performing algebraic operations like addition, subtraction, multiplication, or division on the functions.

  • What does the process of distributing a coefficient within a function look like in the context of composite functions?

    -In the context of composite functions, distributing a coefficient involves multiplying the coefficient by each term inside the function before combining like terms, as seen in the step from 3(x^2 - 3) - 4 to 3x^2 - 13.

  • What is the significance of correctly squaring a binomial in the calculation of composite functions?

    -Correctly squaring a binomial is crucial in the accurate calculation of composite functions, as it affects the outcome of the function composition. Any mistake in this step can lead to incorrect results for the entire composition.

Outlines
00:00
📚 Introduction to Composite Functions

This paragraph introduces the concept of composite functions in mathematics. It explains how to represent composite functions using function notation, distinguishing between f(g(x)) and fg(x). The lesson begins with defining two functions, f(x) = 3x - 4 and g(x) = x^2 - 3, and then proceeds to calculate the composite function f(g(x)). The process involves replacing the x in f(x) with the expression for g(x), leading to the calculation of 3(x^2 - 3) - 4, which simplifies to 3x^2 - 13. The paragraph then explains how to find g(f(x)) by reversing the roles of f and g, using the new functions f(x) = 5x + 2 and g(x) = x^3. It demonstrates the evaluation of g(f(x)) by first calculating g(x) and then substituting the result into f(x), ultimately arriving at the expression 9x^2 - 24x + 13. The explanation includes a step-by-step breakdown of the calculations, ensuring a clear understanding of the process.

Mindmap
Keywords
💡composite functions
Composite functions are a mathematical concept where one function is applied to the result of another function. In the context of the video, it is the primary topic being discussed. For example, if we have a function f(x) = 3x - 4 and another function g(x) = x^2 - 3, the composite function f(g(x)) would mean we apply the function f to the result of g(x).
💡function composition
Function composition is the process of calculating the result of a composite function. It involves nesting one function inside another, as demonstrated in the video where f(g(x)) is computed by substituting the inner function g(x) into the outer function f(x).
💡distribute
In mathematics, to distribute means to multiply a term outside of parentheses by each term inside the parentheses. In the video, this operation is used when calculating f(g(x)) for the function f(x) = 3x - 4 and g(x) = x^2 - 3, where the 3 is distributed over the terms in the parentheses (x^2 and -3).
💡FOIL
FOIL is a method used to expand the product of two binomials (expressions with two terms). It stands for First, Outer, Inner, Last, which refers to the terms to be multiplied in each step. In the video, FOIL is used when calculating g(f(x)) where f(x) = 5x + 2 and g(x) = x^3 - 4, specifically when expanding (3x - 4)^2.
💡evaluate
To evaluate a function means to find its value for a specific input. In the video, this is done by substituting a given value for the variable in the function and simplifying the expression to get the result.
💡variable
In mathematics, a variable is a symbol that represents a number that can change. In the context of the video, variables like x are used in the functions f(x) and g(x) to indicate the input that the functions operate on.
💡squared
The term 'squared' refers to the operation of multiplying a number by itself. In the context of the video, squaring a variable or an expression is part of defining the functions g(x) and calculating their values.
💡cubed
Cubed means raising a number to the third power, which involves multiplying the number by itself three times. In the video, cubing is used when defining the function g(x) in the example with f(x) = 5x + 2.
💡substitute
Substitution in mathematics is the process of replacing one value or expression with another. In the video, substitution is used to calculate the values of composite functions by replacing the variable in one function with the entire expression of another function.
💡simplify
Simplification in mathematics involves making a complex expression easier to understand by reducing it to a more straightforward form. In the video, simplification is the final step after performing operations like distributing or applying the FOIL method to make the expressions more manageable and to find the final answer.
💡negative
A negative number is a number that is less than zero. In the context of the video, negative numbers are used as coefficients or as entire values in the functions, and they play a role in the calculations and final results.
Highlights

Introduction to composite functions and their mathematical representation.

Definition of f(x) as 3x - 4 and g(x) as x^2 - 3.

Explanation of the difference between composite functions and multiplication of functions.

Procedure to find f(g(x)) by substituting g(x) into f(x).

Calculation of f(g(x)) as 3(x^2 - 3) - 4, resulting in 3x^2 - 13.

Process of finding g(f(x)) by substituting f(x) into g(x).

Expansion of (3x - 4)^2 to find g(f(x)), resulting in 9x^2 - 24x + 13.

Example of evaluating f(x) at a specific value, with f(x) = 5x + 2 and g(x) = x^3 - 4.

Determination of g(2) which equals 4 by substituting x with 2 in g(x).

Evaluation of f(g(2)) by substituting g(2) into f(x), resulting in f(4) = 22.

Illustration of evaluating g(f(x)) with x replaced by -1, leading to g(f(-1)) = -31.

Explanation of how to evaluate composite functions by substitution and simplification.

Use of the distributive property in expanding expressions for composite functions.

Demonstration of the FOIL method in expanding binomial expressions.

Clarification of the order of operations in composite functions (first function, then the second).

Importance of understanding the notation and symbols in composite functions (open circle for composition, closed circle for multiplication).

Practical application of composite functions in solving mathematical problems.

Step-by-step guide on how to evaluate composite functions, making it accessible for learners.

Transcripts

Browse More Related Video

How To Evaluate Composite Functions Using Function Tables | Precalculus

Composite Function Explained - The Basics You NEED To Know!

Composite Functions

Function Operations

10 - What are Composite Functions? (Part 1) - Evaluating Composition of Functions & Examples

Composite and Inverse Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsComposite FunctionsFunction EvaluationAlgebraEducationMath TutorialMathematics EducationStep-by-Step GuideMath ConceptsLearning