Calculus AB/BC – 6.10 Integrating Functions Using Long Division and Completing the Square

The Algebros

7 Jan 202117:14

EducationalLearning

32 Likes 10 Comments

TLDRIn this engaging lesson, Mr. Bean tackles advanced algebra 2 topics: completing the square and long division of polynomials. He emphasizes the importance of these techniques in simplifying integrands for integration, especially when direct integration is not feasible. The video offers a step-by-step walkthrough of long division and synthetic division, demonstrating how to handle various polynomial divisions. Mr. Bean also delves into completing the square, showing how it can transform complex expressions into integrable forms. The lesson is a must-watch for those seeking to master these algebraic manipulations and their applications in calculus.

Takeaways

📚 The lesson focuses on applying long division and completing the square to manipulate polynomials for integration.
🔗 For those unfamiliar with long division or completing the square, additional resources are provided in the video description.
🤔 Long division and synthetic division are introduced as methods to simplify polynomials, with synthetic division applicable for linear divisors in the form of x - a.
📊 An example of long division is walked through, demonstrating how to divide a cubic polynomial by a linear polynomial.
📈 The result of the long division is used to find the antiderivative, showcasing the process of integrating each term.
🔄 Synthetic division is shown as a more efficient method for dividing when the divisor is linear, with a step-by-step example provided.
🧩 Completing the square is explained as a technique to create perfect squares in quadratic expressions, which simplifies integration.
🔢 A detailed example of completing the square is given, transforming a quadratic expression into a form that can be easily integrated.
🌐 The concept of u-substitution is introduced for more complex integrals, with an example involving a natural log function.
💡 Recognizing when to use long division, completing the square, or u-substitution is emphasized as an important skill for solving difficult integrals.
🚀 The lesson concludes with a challenging example modeled after AP exam problems, demonstrating the application of the techniques learned.

Q & A

What is the main topic of the lesson?
-The main topic of the lesson is completing the square and long division polynomial in the context of algebra 2.
Why are completing the square and polynomial long division important in integration?
-Completing the square and polynomial long division are important in integration because they help manipulate the integrand into a form that can be integrated, especially when the integrand is not immediately integrable.
What is the significance of the integrand in the context of this lesson?
-The integrand is significant because it is the part of the integral that we take the anti-derivative of. Manipulating the integrand through completing the square and polynomial long division can make it easier to find the anti-derivative.
What is synthetic division, and when can it be used?
-Synthetic division is a shorthand method for dividing a polynomial by a linear factor of the form x - a. It can be used when the divisor is linear and there is no coefficient in front of the x term.
How does long division work in polynomials?
-Long division in polynomials involves dividing the dividend (the polynomial to be divided) by the divisor (another polynomial), similar to how division works with numbers. You divide the leading term of the dividend by the leading term of the divisor, multiply the divisor by the result, subtract it from the dividend, and bring down the next term to continue the process.
What is the purpose of completing the square in the context of the lesson?
-Completing the square is used to rewrite a quadratic expression in a form that allows for easier integration. It involves adding and subtracting the square of half the coefficient of the linear term to the quadratic expression.
How does the讲师 (lecturer) demonstrate the application of completing the square?
-The lecturer demonstrates the application of completing the square by showing how to rewrite the denominator of an integral in a form where it becomes a perfect square, which can then be integrated using inverse trigonometric functions.
What is the role of u-substitution in integration?
-U-substitution is a technique used in integration to simplify the integrand by replacing a part of it with a new variable, u. This can make the integral easier to solve, especially when dealing with complex fractions or expressions involving inverse trigonometric functions.
What is the significance of recognizing patterns in integration?
-Recognizing patterns in integration is crucial because it helps determine the appropriate method to use for solving a given integral. It can make the process more efficient and less prone to errors.
How does the讲师 (lecturer) address the challenge of recognizing when to use certain techniques in integration?
-The lecturer acknowledges that recognizing when to use certain techniques like completing the square or u-substitution is a key skill that students need to develop. The lecturer plans to discuss this in the last lesson of the unit, focusing on pattern recognition.
What is the final challenging problem presented in the lesson?
-The final challenging problem involves a complex integral with a denominator that requires completing the square and u-substitution to simplify and solve. The lecturer walks through the process of transforming the integrand into a form that can be integrated using the tangent inverse function.

Outlines

00:00

📚 Introduction to Completing the Square and Long Division

This paragraph introduces the topic of completing the square and long division in the context of algebra 2. Mr. Bean explains that the lesson will not teach these methods from scratch but may remind those who already know them. He emphasizes the importance of these techniques in manipulating the integrand for integration, particularly when the integrand cannot be directly integrated. Mr. Bean also mentions that resources will be provided for those who need to learn these methods from the beginning.

05:01

📝 Long Division and Synthetic Division Examples

In this paragraph, Mr. Bean walks through the process of long division, using an example to illustrate how to divide a polynomial. He then explains synthetic division, a shortcut method for dividing when the divisor is linear. The paragraph includes a step-by-step demonstration of both methods, highlighting when to use each one and how they can simplify the process of finding the integral of a polynomial.

10:01

🔢 Advanced Techniques: U-Substitution and Completing the Square

This paragraph delves into more advanced mathematical techniques, including u-substitution and completing the square. Mr. Bean provides a detailed explanation of how to apply these methods to complex integrals, transforming them into more manageable forms. The paragraph includes a challenging example that requires both long division and u-substitution, demonstrating the process of solving complex problems in calculus.

15:02

🧠 Mastering the Concepts: AP Exam-Style Problems

The final paragraph focuses on preparing for the AP exam by tackling a problem similar to those found on the exam. Mr. Bean guides the audience through the process of completing the square and using u-substitution to solve a difficult integral. He emphasizes the importance of recognizing when to apply these techniques and encourages practice to master the concepts for the AP exam.

Mindmap

Keywords

💡Completing the Square

Completing the square is a technique used in algebra to transform a quadratic equation into a perfect square trinomial, making it easier to solve or integrate. In the video, this method is highlighted as essential for manipulating the integrand in calculus, particularly when integrating functions that cannot be directly integrated. The process involves adding and subtracting a particular value (half of the linear coefficient squared) to complete the square. The narrator emphasizes its importance for calculus students, especially in preparing for situations where this technique simplifies the integration process.

💡Polynomial Long Division

Polynomial long division is a method for dividing a polynomial by another polynomial of lesser or equal degree, much like long division with numbers. In the context of the video, it's introduced as a precursor to understanding how to manipulate algebraic expressions in calculus. The video's narrator, Mr. Bean, demonstrates this technique as a way to simplify expressions before integrating, showing its utility in breaking down more complex polynomials into simpler parts that can be more easily integrated.

💡Integrand

The integrand is the function that is to be integrated, positioned inside the integral sign and before the differential, such as 'dx'. In the video, understanding and manipulating the integrand through completing the square and polynomial long division is stressed as crucial for calculus students. This is because the integrand's form can significantly affect the ease or possibility of performing the integration, and these algebraic techniques can transform the integrand into a more manageable form.

💡Synthetic Division

Synthetic division is presented as a faster, simpler alternative to polynomial long division when dividing by a linear divisor. It involves less writing and fewer calculations. The video illustrates how to use synthetic division for divisors of the form x - a, where 'a' is a constant, demonstrating its efficiency and suggesting its use when applicable. This technique, alongside polynomial long division, is shown as a valuable tool for preparing the integrand for integration.

💡Anti-derivative

The anti-derivative, or indefinite integral, of a function is a function whose derivative is the original function. In the video, taking the anti-derivative is the goal of manipulating the integrand through algebraic methods. Mr. Bean illustrates how after simplifying expressions using completing the square and polynomial long division, one can more easily find the anti-derivatives, demonstrating the connection between algebraic manipulation and integral calculus.

💡U-Substitution

U-substitution is a technique used to simplify the process of finding the integral of a function. It involves changing the variables in an integral to make it easier to integrate. In the video, u-substitution is employed after completing the square and polynomial long division to simplify the integral further. This shows the method's relevance in solving integrals that initially seem complicated, emphasizing its role in integral calculus.

💡Coefficient

A coefficient in algebra is a numerical or constant quantity placed before and multiplying the variable in an algebraic term. The video highlights the importance of coefficients in completing the square and polynomial long division, explaining how these values influence the steps and outcomes of these processes. The manipulation of coefficients is shown to be key in preparing functions for integration.

💡Placeholder

A placeholder in the context of polynomial long division, as mentioned in the video, is a zero term added to ensure each degree of the variable is represented, even if it originally lacks a coefficient in the polynomial. This concept is important for correctly applying polynomial long division, as it ensures that the division process accounts for all degrees of the polynomial being divided, thus accurately preparing the expression for further operations like integration.

💡Inverse Trig Functions

Inverse trigonometric functions, such as arc tangent or sine inverse, are functions that reverse the action of the trigonometric functions. In the video, these functions appear as results of integrating certain forms of functions obtained after completing the square. This highlights the interplay between algebraic manipulation and calculus, demonstrating how algebraic techniques can lead to integrals that result in inverse trigonometric functions.

💡Natural Logarithm

The natural logarithm, denoted as ln, is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.71828. In the calculus video, the natural logarithm arises as part of the anti-derivative of certain functions that have been manipulated using algebraic techniques like polynomial long division. This emphasizes the diversity of outcomes when integrating different functions and the importance of these algebraic techniques in facilitating the integration process.

Highlights

Introduction to the lesson on completing the square and long division polynomial in algebra 2.

Clarification that the lesson assumes prior knowledge of the topics and provides resources for those unfamiliar.

Explanation of the importance of completing the square and long division in relation to the integrand in calculus.

Demonstration of long division with a polynomial, including the step-by-step process.

Use of synthetic division for simpler problems with a linear divisor.

Example of how to take the anti-derivative after performing long division.

Reiteration of the lesson's purpose and the application of long division and completing the square in calculus.

Detailed walkthrough of a complex integral problem using long division and u-substitution.

Introduction to completing the square with a focus on the quadratic term and linear term.

Illustration of completing the square with a negative coefficient in front of x squared.

Example of completing the square with a radical in the denominator.

Explanation of how to handle a complex integral with both long division and completing the square.

Demonstration of recognizing when to use completing the square during problem-solving.

Presentation of a challenging problem similar to those found on AP exams.

Solution to the challenging problem using completing the square and u-substitution.

Conclusion of the lesson with encouragement for further practice and mastery.

Transcripts

Browse More Related Video

Calculus AB/BC – 1.6 Determining Limits Using Algebraic Manipulation

Calculus AB/BC – 1.7 Selecting Procedures for Determining Limits

Integral of a Quotient

Factoring Polynomials - By GCF, AC Method, Grouping, Substitution, Sum & Difference of Cubes

Polynomials - Long Division

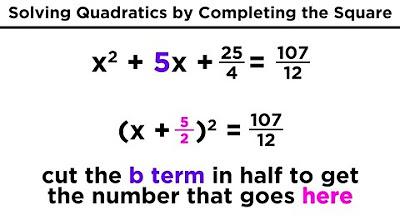
Solving Quadratics by Completing the Square

Calculus AB/BC – 6.10 Integrating Functions Using Long Division and Completing the Square

Takeaways

Q & A

What is the main topic of the lesson?

Why are completing the square and polynomial long division important in integration?

What is the significance of the integrand in the context of this lesson?

What is synthetic division, and when can it be used?

How does long division work in polynomials?

What is the purpose of completing the square in the context of the lesson?

How does the讲师 (lecturer) demonstrate the application of completing the square?

What is the role of u-substitution in integration?

What is the significance of recognizing patterns in integration?

How does the讲师 (lecturer) address the challenge of recognizing when to use certain techniques in integration?

What is the final challenging problem presented in the lesson?