Polynomials - Long Division
TLDRThis instructional video offers a step-by-step guide on performing long division with polynomials. Starting with basic examples, it progressively tackles more complex problems, teaching viewers how to set up the divisor and dividend, execute division, multiplication, and subtraction to find the quotient. The video also demonstrates how to handle missing terms in polynomials by introducing zeros and concludes with a detailed example dividing a fifth-degree polynomial by a trinomial, including how to manage remainders. The host encourages viewers to practice and subscribe for more educational content on various math and science topics.
Takeaways
- 📚 The video provides a step-by-step tutorial on long division with polynomials.
- 📈 The tutorial progresses from easier to more complex problems to help viewers grasp the concept.
- 🔍 The first example involves dividing a quadratic polynomial by a linear polynomial, resulting in a simple linear quotient.
- 📝 The process includes steps like dividing, multiplying, and subtracting to simplify the polynomial expression.
- ✅ The video demonstrates how to check the work by multiplying the quotient by the divisor to see if it matches the original dividend.
- 📉 The second example shows division of a polynomial with a higher degree by a linear polynomial, resulting in a quotient with a remainder.
- 📘 It explains how to handle cases where terms are missing in the polynomial, by including zero coefficients for those terms.
- 🔢 The third example involves dividing a quartic polynomial by a quadratic polynomial, illustrating the process with a detailed example.
- 📚 The video covers division of polynomials with higher degrees and includes remainders in the final answers.
- 📝 The final example demonstrates dividing a quintic polynomial by a quadratic polynomial, showing the inclusion of remainders in the solution.
- 👍 The video encourages viewers to subscribe for more math and science content, indicating a range of topics covered by the channel.
Q & A
What is the main topic of the video?
-The main topic of the video is how to use long division with polynomials.
What is the first polynomial division problem presented in the video?
-The first polynomial division problem is to divide x^2 + 9x + 20 by x + 5.
What is the quotient of the first division problem in the video?
-The quotient of the first division problem is x + 4.
What is the process of long division with polynomials as explained in the video?
-The process involves dividing the leading term of the dividend by the leading term of the divisor, multiplying the divisor by the result, subtracting from the dividend, and repeating the process with the new polynomial until the degree of the remainder is less than the divisor.
How does the video suggest checking the work after performing polynomial long division?
-The video suggests multiplying the quotient by the divisor and checking if the result matches the original dividend.
What is the second polynomial division problem presented in the video?
-The second polynomial division problem is to divide 6x^2 + 7x - 20 by 2x + 5.
What is the quotient of the second division problem in the video?
-The quotient of the second division problem is 3x - 4.
What is the significance of including zero terms when the polynomial has missing degrees?
-Including zero terms for missing degrees ensures that the polynomial is represented correctly and allows for accurate division.
How does the video handle division when the degree of the remainder is less than the divisor?
-When the degree of the remainder is less than the divisor, the division stops, and the remainder is included in the final answer.
What is the final example problem presented in the video?
-The final example problem is to divide x^5 + 2x^4 + x^3 - x^2 - 22x - 15 by x^2 + 2x - 3.
What is the final answer format when there is a remainder in polynomial long division?
-The final answer includes the quotient and the remainder over the divisor, written as 'quotient + remainder/ divisor'.
Outlines
📚 Introduction to Polynomial Long Division
The video begins with an introduction to polynomial long division, emphasizing the importance of watching the entire video for a progressive understanding of the topic. The first example involves dividing a quadratic polynomial, x^2 + 9x + 20, by a linear polynomial, x + 5. The process is explained step by step, starting with setting up the problem, performing the division, multiplication, and subtraction to arrive at the quotient, x + 4, and confirming the remainder is zero. The method is then applied to a second example, dividing 6x^2 + 7x - 20 by 2x + 5, resulting in a quotient of 3x - 4. The video demonstrates how to check the work by multiplying the quotient by the divisor and verifying it equals the original dividend.
🔍 Verifying Polynomial Division
This paragraph focuses on the verification process of polynomial division. It uses the example of multiplying 3x - 4 by 2x + 5 to demonstrate how to check the correctness of the division. The multiplication is carried out step by step, resulting in the original dividend, 6x^2 + 7x - 20, confirming the division was done correctly. The video then moves on to tackle a more complex polynomial division problem involving a quartic polynomial divided by a quadratic polynomial, with the setup and initial steps of the division process being outlined.
📘 Complex Polynomial Division with Missing Terms
The video script continues with a complex example of polynomial long division, where the polynomial 6x^4 - 30x^2 + 0x^3 + 0x + 24 is divided by 2x^2 - 8. The process involves handling missing terms by including zero coefficients for those terms. The division begins by dividing the leading term of the dividend by the leading term of the divisor, resulting in a quotient term. The script then describes the multiplication of this term by the divisor and the subsequent subtraction to simplify the expression. The process is repeated until the remainder is obtained, leading to the final quotient of 3x^2 - 3.
📘 Dividing Polynomials with Higher Exponents and Remainders
The final paragraph of the script introduces an even more challenging polynomial division problem, where a fifth-degree polynomial is divided by a trinomial. The division process is detailed, starting with dividing the highest degree term of the dividend by the highest degree term of the divisor. The script explains the multiplication of the resulting quotient term by the divisor and the subtraction from the dividend to simplify the expression. The process is iteratively applied to each term, with attention to changing signs during subtraction. The video concludes with obtaining a quotient and a remainder, illustrating how to express the final answer when a remainder is present.
🎉 Conclusion and Encouragement to Explore More
In the concluding paragraph, the video script summarizes the process of dividing polynomials using long division and encourages viewers to apply the method to various problems. It also invites viewers to subscribe for more educational content, mentioning the range of topics covered in other videos, such as chemistry, physics, algebra, trigonometry, pre-calculus, and calculus. The script emphasizes the importance of practice and provides a final thank you for watching the video.
Mindmap
Keywords
💡Long Division
💡Polynomials
💡Dividend
💡Divisor
💡Quotient
💡Remainder
💡Exponents
💡Coefficients
💡Like Terms
💡Subtraction
💡Multiplication
Highlights
Introduction to long division with polynomials, starting with easy problems and progressively getting harder.
Setting up the long division problem with the divisor on the outside and the dividend on the inside.
Dividing x squared by x to obtain x as the first term of the quotient.
Multiplying the first term of the quotient by the divisor and subtracting it from the dividend.
Finding the remainder after the first subtraction step.
Continuing the division process by dividing the new leading term by the divisor.
Multiplying and subtracting to find the next term of the quotient and the new remainder.
Completing the division to find the quotient x plus 4 for the given polynomial example.
Demonstrating another example with a polynomial divided by a binomial, emphasizing the division, multiplication, and subtraction steps.
Using the FOIL method to check the work by multiplying the quotient by the divisor.
Presenting a more complex example with a higher degree polynomial and a missing term, illustrating the inclusion of zero coefficients.
Dividing a higher degree polynomial by a binomial, showing the process of subtracting exponents and multiplying terms.
Handling a remainder when the degree of the divisor is higher than the degree of the current term.
Dividing a fifth-degree polynomial by a trinomial, detailing the step-by-step process.
Correcting a mistake during the division process and continuing with the correct steps.
Finalizing the division with a quotient and remainder, and explaining how to write the answer with the remainder included.
Encouraging viewers to subscribe for more math and science videos covering various topics.
Transcripts
Browse More Related Video

How To Use Synthetic Division on Any Polynomial!

Long Division With Polynomials - The Easy Way!

Terminology for the basic operations and writing algebraic expressions from words

Finding ALL Solutions of Polynomials (Precalculus - College Algebra 37)

Math Antics - Long Division
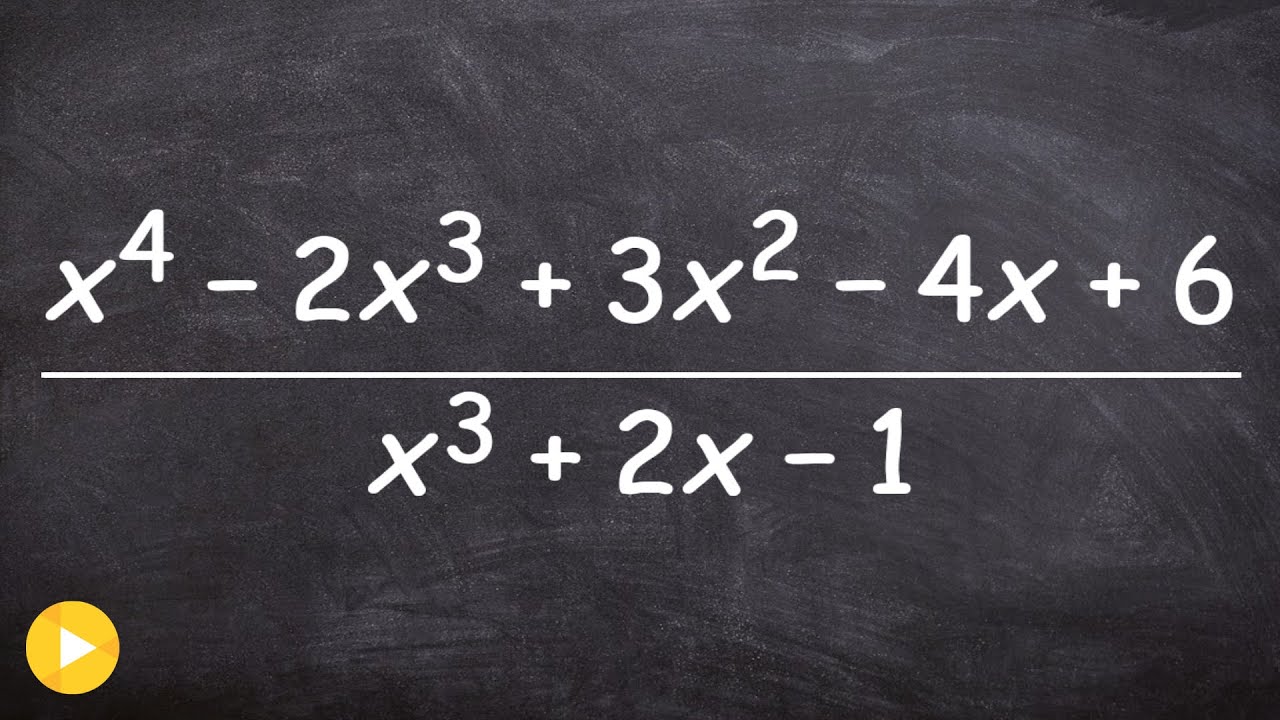
How to divide a trinomial into a polynomial using long division
5.0 / 5 (0 votes)
Thanks for rating: