Calculus AB/BC – 1.6 Determining Limits Using Algebraic Manipulation

The Algebros
28 Aug 202011:03
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging calculus lesson, Mr. Bean teaches algebraic manipulation to find limits. Starting with direct substitution, he simplifies limits by plugging in values. He then covers factoring and canceling to handle indeterminate forms, demonstrating how to simplify expressions before applying direct substitution. Mr. Bean also explores non-existent limits, showing how algebraic manipulation reveals their absence. The lesson concludes with special trigonometric limits, emphasizing the approach to one for sine over x and zero for 1 - cos(x) over x, providing shortcuts for solving these common problems efficiently.

Takeaways
  • 📚 Direct Substitution: The simplest method to find a limit is by substituting the value of x that the limit approaches into the expression to find the y-value.
  • 📈 Constant Limits: When the expression simplifies to a constant, regardless of the value of x, the limit is that constant value, as seen with y = 6.
  • 🔍 Indeterminant Form: An expression like 0/0 indicates an indeterminant form, which requires algebraic manipulation to find the limit.
  • 🔄 Factor and Cancel: Factoring out common terms in the numerator and denominator can simplify expressions and resolve indeterminant forms.
  • 📉 Limits at Holes: Even if an expression cannot be simplified to find a limit directly, like at x = 0 in the example, the limit can still be determined by looking at the behavior of the function from both sides of the hole.
  • 🔢 Simplification Before Substitution: Simplifying the expression before direct substitution can make it easier to find the limit, especially when dealing with complex fractions.
  • 🚫 Non-Existent Limits: If an expression cannot be simplified to allow for direct substitution, such as when x approaches a value that makes the denominator zero without canceling, the limit does not exist.
  • 📉 Asymptotes and Limits: Understanding the behavior of functions near vertical asymptotes helps in determining when limits do not exist due to the function approaching infinity or negative infinity.
  • 📚 Special Trig Limits: Certain trigonometric limits, like sin(x)/x as x approaches 0, have specific values and should be memorized for quick problem-solving.
  • 🔢 Trigonometric Manipulation: Multiplying the numerator and denominator by the same trigonometric function can simplify limits involving trigonometric expressions.
  • 📐 Difference of Squares: Recognizing and applying the difference of squares formula can simplify trigonometric limits, as shown with cos^2(x) - 1 factored into (cos(x) - 1)(cos(x) + 1).
Q & A

  • What is the main topic of the lesson presented by Mr. Bean?

    -The main topic of the lesson is algebraic manipulation to find limits in calculus.

  • What is the first method Mr. Bean introduces to find limits?

    -The first method introduced is direct substitution, where you plug in the value of x that the limit is approaching into the expression.

  • What is the result of the limit as x approaches -1 for the expression x^2 + 2x - 4?

    -The result of the limit as x approaches -1 for the expression x^2 + 2x - 4 is -5.

  • How does the graph of the expression x^2 + 2x - 4 behave as x approaches -1?

    -The graph of the expression x^2 + 2x - 4 is a parabola, and as x approaches -1, the y-value approaches -5.

  • What is the limit of the expression y = 6 as x approaches 2?

    -The limit of the expression y = 6 as x approaches 2 is 6, since it is a constant value and does not depend on x.

  • What is an indeterminate form in calculus?

    -An indeterminate form in calculus occurs when an expression results in 0/0 or similar undefined forms, which cannot be directly evaluated.

  • How does Mr. Bean suggest simplifying the limit as x approaches 0 for the expression (x(x - 5))/(x - 4)?

    -Mr. Bean suggests factoring out an x from the numerator and then canceling the common x terms with the denominator, leaving 4x - 5, which simplifies to -5 after direct substitution of x = 0.

  • What is the limit as x approaches -7 for the expression (2x^2 + x - 7)/(x + 7) after factoring?

    -After factoring, the limit as x approaches -7 for the expression simplifies to 2x - 1, and upon direct substitution, it results in -15.

  • How can you determine if a limit does not exist?

    -A limit does not exist if, after simplification, you cannot plug in the value of x that the limit is approaching, or if the left and right sides of the point do not approach the same value.

  • What is a special trigonometric limit that Mr. Bean discusses?

    -Mr. Bean discusses the special trigonometric limit of sin(x)/x as x approaches 0, which approaches 1.

  • How does Mr. Bean suggest memorizing the trigonometric limits for sin(x)/x and 1 - cos(x)/x?

    -Mr. Bean suggests associating the sine function with the number 1 and the cosine function with the number 0 to help memorize that sin(x)/x approaches 1 and 1 - cos(x)/x approaches 0 as x approaches 0.

  • What is the result of the limit as x approaches 0 for the expression 3sin(3x)/x?

    -The result of the limit as x approaches 0 for the expression 3sin(3x)/x is 3, by using the special trigonometric limit for sin(x)/x.

  • How does Mr. Bean explain the limit of the expression (sin(7x) - sin(9x))/(x^2) as x approaches 0?

    -Mr. Bean explains that by separating the fraction and multiplying both the numerator and denominator by x, the limit simplifies to 7/9, using the special trigonometric limits.

  • What is the result of the limit as x approaches 0 for the expression cos^2(x) - 1/x?

    -The result of the limit as x approaches 0 for the expression cos^2(x) - 1/x is 0, after factoring it as a difference of squares and canceling terms.

Outlines
00:00
📚 Introduction to Algebraic Manipulation in Calculus

In this calculus lesson, Mr. Bean introduces the concept of algebraic manipulation to find limits of functions. He begins with the basic technique of direct substitution, demonstrating how to evaluate limits by simply plugging in the value that x approaches into the function. The example given is a quadratic function, where as x approaches -1, the limit is found to be -5 by direct substitution. Mr. Bean also explains that for constant functions, like y = 6, the limit is the constant value itself. The lesson then moves on to more complex scenarios where direct substitution is not possible due to indeterminate forms, such as 0/0. In such cases, algebraic manipulation like factoring and cancellation is required to simplify the expression before finding the limit.

05:01
🔍 Exploring Indeterminate Forms and Factoring Techniques

This section of the video script delves deeper into handling indeterminate forms that arise when attempting direct substitution results in 0/0. Mr. Bean illustrates how to factor expressions to simplify them and make direct substitution possible. He provides an example where factoring out an x from the numerator and recognizing common factors with the denominator allows for cancellation, leading to a simplified expression whose limit can be found by direct substitution. The script also includes a discussion on limits that do not exist, showing how algebraic manipulation can reveal that the left and right limits approach different values, indicating the absence of a limit. Graphs are used as visual aids to understand the behavior of functions at certain points, especially near vertical asymptotes.

10:03
📉 Understanding Trigonometric Limits and Special Cases

The final part of the script focuses on trigonometric limits, specifically the behavior of sine and cosine functions as they approach certain values. Mr. Bean explains the special limits of sine x over x and x over sine x as x approaches zero, both of which tend to one. He also covers the limit of 1 - cosine x over x, which approaches zero. The script emphasizes the importance of recognizing these special cases and provides mnemonic devices to remember the outcomes of these limits. Additionally, Mr. Bean demonstrates how to manipulate trigonometric expressions to simplify them and apply these special limits, showing examples of how to factor and adjust expressions to reveal the underlying simple limits. The lesson concludes with a preview of more complex manipulation techniques to be covered in future lessons.

Mindmap
Keywords
💡Algebraic Manipulation
Algebraic manipulation refers to the process of transforming algebraic expressions into different but equivalent forms to simplify calculations or to make the expression more understandable. In the video's context, it is used to find limits by changing the form of the expression, such as factoring and canceling terms, which is essential for understanding how to approach limits that cannot be solved by direct substitution.
💡Limit
A limit in calculus is the value that a function or sequence approaches as the input (often denoted as 'x') approaches a certain value. The video focuses on finding these limits through various algebraic techniques. For example, the script discusses the limit as x approaches -1 for the expression x^2 + 2x - 4, which is found by direct substitution, resulting in a limit of -5.
💡Direct Substitution
Direct substitution is a method used to find the limit of a function by simply substituting the value that the variable is approaching into the function. The video demonstrates this with the example of a constant function where the limit as x approaches 2 is 6, as the function value does not depend on x and remains constant.
💡Indeterminant Form
An indeterminant form arises when an expression simplifies to 0/0 or undefined expressions like ∞/∞ after direct substitution. The video explains that when this occurs, algebraic manipulation is necessary to find the limit. For instance, when trying to find the limit as x approaches 0 for the expression x/(x+1), direct substitution results in an indeterminant form, prompting the need for further manipulation.
💡Factor and Cancel
Factor and cancel is a technique used to resolve indeterminant forms by factoring expressions and canceling out common terms. The video illustrates this with an example where the numerator and denominator are factored, allowing for the cancellation of terms, which simplifies the expression and makes it possible to find the limit through direct substitution.
💡Graph
In the context of the video, a graph represents the visual representation of a function or set of functions, showing the relationship between the input (x) and output (y) values. The script uses graphs to illustrate the behavior of functions as x approaches certain values, such as showing a parabola and its limit at x = -1, or a constant function represented by a horizontal line.
💡Trig Limits
Trig limits refer to the limits involving trigonometric functions. The video discusses special cases, such as the limit of sin(x)/x as x approaches 0, which is a common trigonometric limit that equals 1. These limits are important in understanding the behavior of trigonometric functions near certain points.
💡Sine and Cosine Functions
Sine and cosine are fundamental trigonometric functions that relate the angles of a right triangle to the ratios of its sides. In the video, these functions are used in the context of limits, such as sin(x)/x approaching 1 as x approaches 0, which is a key concept in trigonometric limit problems.
💡Difference of Squares
The difference of squares is an algebraic identity that states that the difference between the squares of two expressions can be factored into the product of the sum and difference of the two expressions (a^2 - b^2 = (a+b)(a-b)). The video uses this identity to simplify the expression cos^2(x) - 1, which factors into (cos(x) + 1)(cos(x) - 1), allowing for further manipulation to find the limit as x approaches 0.
💡Asymptote
An asymptote is a line that a curve approaches but never intersects. In the context of the video, vertical asymptotes are mentioned, which occur when the denominator of a rational function is zero, and the function approaches infinity or negative infinity. The script uses the concept of asymptotes to explain why certain limits do not exist, as seen in the example where the limit as x approaches -6 does not exist due to the vertical asymptote at that point.
Highlights

Introduction to algebraic manipulation in calculus for finding limits.

Direct substitution method explained with an example.

Demonstration of direct substitution resulting in the limit of -5.

Graphical representation of a parabola and its limit as x approaches -1.

Explanation of constant limits and their graphical representation.

Indeterminant form identified and the need for algebraic manipulation.

Factoring technique to resolve indeterminant forms in limits.

Example of factoring and canceling to simplify a limit expression.

Limit of a simplified expression using direct substitution.

Graphical explanation of a function with a hole at x=0 and its limit.

Factoring a rational function and its limit as x approaches -7.

Graphical representation of a function with a hole and its limit.

Identifying limits that do not exist through algebraic manipulation.

Explanation of vertical asymptote and non-existent limits.

Special trigonometric limits involving sine and cosine functions.

Memorization tips for trigonometric limits with sine and cosine.

Shortcut method for calculating limits with sine and cosine functions.

Example of applying the shortcut method to a trigonometric limit.

Difference of squares factoring technique in trigonometric limits.

Conclusion of the lesson with a preview of the next topic.

Transcripts

Browse More Related Video

Calculus AB/BC – 1.7 Selecting Procedures for Determining Limits

AP Calculus AB - 1.6b Determining Limits Using Algebraic Manipulation

Calculus AB/BC – 1.8 Determining Limits Using the Squeeze Theorem

Calculus AB/BC – 1.14 Infinite Limits and Vertical Asymptotes

Calculus AB/BC – 1.4 Estimating Limit Values from Tables

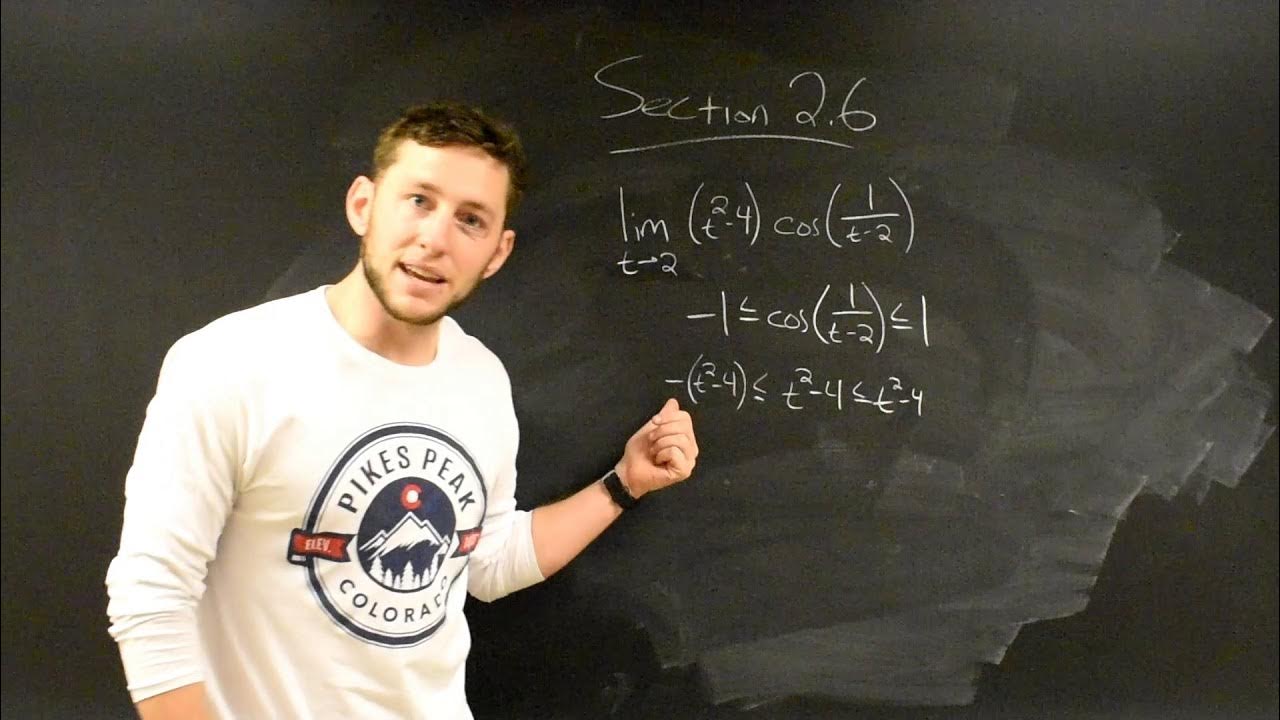
Limits Involving Sine and Cosine & The Squeeze Theorem!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Algebraic ManipulationCalculus LessonsDirect SubstitutionFactor and CancelIndeterminant FormTrig LimitsGraph AnalysisLimit ExistenceSine Over XCosine Squared