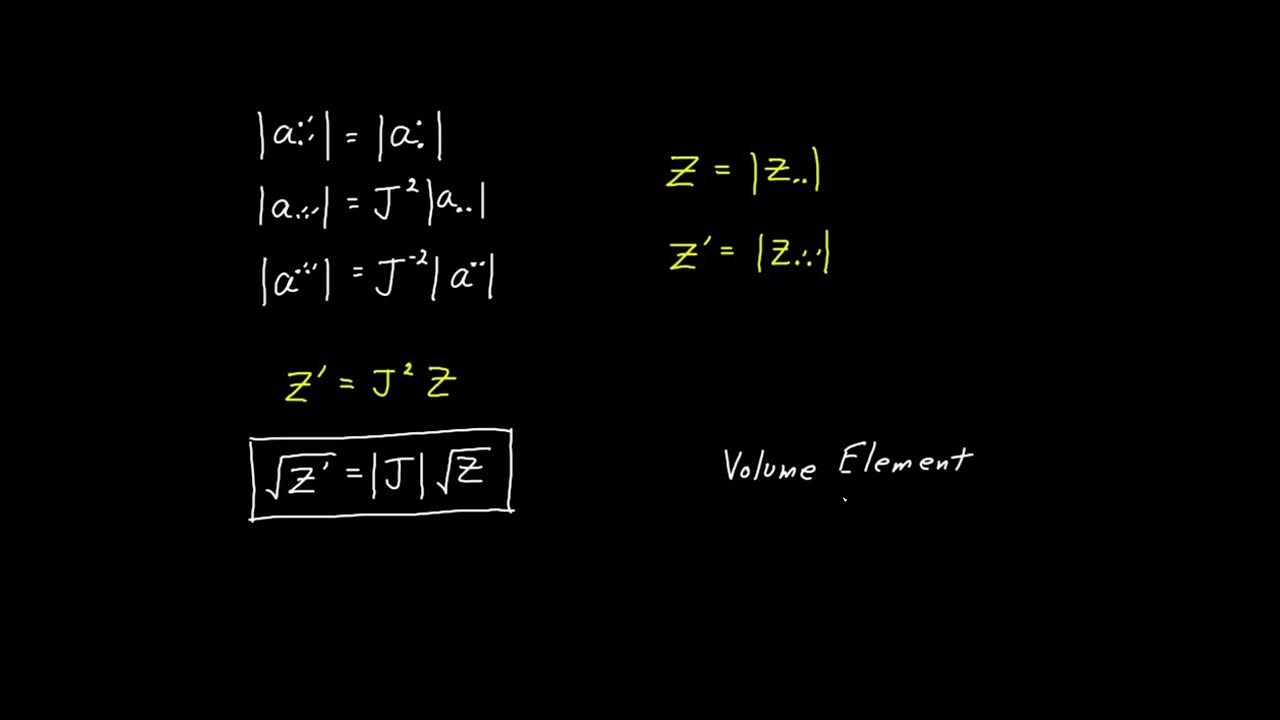Tensor Calculus for Physics Ep. 14 | Covariant Curl
TLDRThis episode of 'Tensor Calculus for Physics' delves into the formal expression of the curl operator in tensor language, highlighting its distinction from divergence and the Laplacian. The video clarifies the concept of tensor density, particularly focusing on the Levi-Civita symbol, which is not a tensor but transforms as one when multiplied by the square root of the metric determinant. The presenter provides a step-by-step derivation of the covariant curl vector in any coordinate system, using spherical coordinates as an example to demonstrate the process. The aim is to offer a deeper understanding of tensor calculus in physics, preparing viewers for upcoming topics on curvature.
Takeaways
- 📚 The video discusses the tensor calculus approach to the differential operator 'curl', emphasizing its unique considerations compared to 'divergence' and 'laplacian'.
- 🌀 The script introduces the concept of 'curl' in tensor language, explaining that it differs from other operators due to its inherent tensor density nature.
- 📏 The video contrasts the approach of the book 'Tensor Calculus for Physics' by Dwight Neuenschwander with a more formal treatment of the subject.
- 🔗 It explains that the Levi-Civita symbol, used in expressing 'curl', is not a tensor but a tensor density, which does not transform as a tensor under coordinate changes.
- 📉 The script revisits the concept of tensor density, illustrating it with the determinant of the metric and the Jacobian, which are scalar densities.
- 🔍 The video clarifies that tensor densities are objects that almost transform as tensors but are multiplied by a power of the Jacobian in the transformation rule.
- 📐 The script demonstrates how to make 'curl' covariant by defining a new tensor, the Levi-Civita tensor, which is a product of the square root of the metric tensor and the Levi-Civita symbol.
- 📝 The video provides a detailed derivation of the covariant curl vector in terms of covariant derivatives and the contravariant Levi-Civita tensor.
- 🌐 The script explains that the curl operator is particularly relevant in three-dimensional space and assumes i, j, k run from one to three in the tensor notation.
- 📈 The video simplifies the expression for the curl vector by showing that connection coefficients in the covariant derivative cancel out, leading to a simplified formula.
- 📚 The video concludes with an example in spherical coordinates to illustrate the application of the derived tensor calculus formula for 'curl'.
Q & A
What is the main topic of the video?
-The main topic of the video is the expression of the curl in the language of tensors within the context of tensor calculus for physics.
Why does the video mention that curl is treated differently from divergence and the Laplacian?
-Curl is treated differently because of the special considerations needed when expressing it in index notation, which involves the Levi-Civita symbol, a tensor density rather than a tensor.
What is a tensor density according to the video?
-A tensor density is an object that almost transforms as a tensor of a given rank but is multiplied by a certain power of the Jacobian in the transformation rule.
Why is the Levi-Civita symbol considered a tensor density?
-The Levi-Civita symbol is considered a tensor density because it transforms with a factor of the Jacobian, which is not the case for a true tensor.
What is the weight of a tensor density?
-The weight of a tensor density is the power to which the Jacobian factor is raised in the transformation rule.
How does the video approach the tensorial representation of curl?
-The video approaches the tensorial representation of curl by defining a new tensor called the Levi-Civita tensor, which is the product of the square root of the metric tensor and the Levi-Civita symbol.
What is the contravariant curl vector defined as in the video?
-The contravariant curl vector is defined as a contravariant vector with components calculated using the Levi-Civita tensor and covariant derivatives of a covariant vector field.
How does the video simplify the expression for the contravariant curl vector?
-The video simplifies the expression by showing that the connection coefficients, or Christoffel symbols, cancel out, leaving a simpler form involving direct derivatives.
What is the significance of the cyclic permutation in the Levi-Civita tensor when calculating curl?
-The cyclic permutation in the Levi-Civita tensor is significant because it anti-symmetrizes the tensor, which is a key property for calculating curl components.
How does the video relate the contravariant curl vector to the ordinary vector?
-The video relates the contravariant curl vector to the ordinary vector by dividing by the square root of the metric component, which is the usual prescription for converting between covariant and contravariant vectors.
What coordinate system is used for the example in the video?
-The video uses spherical coordinates for the example to demonstrate the calculation of a curl component.
Why does the video mention that the curl has limited use outside of three-dimensional space?
-The video mentions this because the Levi-Civita symbol and the concept of curl are inherently tied to three dimensions, making their application in higher dimensions less straightforward.
What is the relationship between the curl component calculated and the field strength tensors in electromagnetism?
-The video explains that the curl components can be related to the field strength tensors in electromagnetism by expressing them in terms of the components of a second-rank tensor.
Outlines
📚 Introduction to Tensor Calculus for Curl
The video script begins with an introduction to an episode on tensor calculus, focusing on the differential operator 'curl'. The speaker mentions that curl will be discussed in a more formal way than in the book 'Tensor Calculus for Physics' by Dwight E. Neuenschwander. The script highlights the need for special considerations when expressing curl in the language of tensors, as opposed to divergence and the Laplacian. The speaker also indicates that any derivations not covered in the video will be linked in the description for further exploration.
🔍 Understanding Tensor Densities and Curl
This paragraph delves into the concept of tensor densities, which are not tensors but transform with a power of the Jacobian. The script explains that the determinant of the metric is a scalar density, and the Levi-Civita symbol (used in the expression for curl) is a tensor density due to its transformation properties. The speaker clarifies that the product of the square root of the metric determinant and the Levi-Civita symbol results in a full-fledged tensor, which is crucial for expressing curl in a generally covariant form.
📘 Defining the Levi-Civita Tensor for Curl
The script introduces the Levi-Civita tensor, defined as the product of the square root of the metric determinant and the Levi-Civita symbol, making it a rank three covariant tensor. The speaker discusses the importance of using covariant and contravariant vectors and tensors for expressing curl in a covariant form. The paragraph also explains the transformation of the Levi-Civita tensor and how it can be used to define the contravariant curl vector component in terms of covariant derivatives and covariant vectors.
🔧 Simplifying the Covariant Curl Expression
The paragraph discusses simplifying the expression for the curl in covariant form. It explains the anti-symmetrization property of the Levi-Civita tensor and how it can be used to simplify the curl expression. The script also addresses the limited applicability of curl and cross products to three-dimensional spaces and provides a simplified formula for the curl component in terms of covariant derivatives and the covariant vector field.
🌐 Applying Curl in Spherical Coordinates
The script provides an example of calculating the curl in spherical coordinates, specifically focusing on the theta component. It demonstrates the process of converting covariant vectors to ordinary vectors and applying the curl formula derived earlier. The example illustrates how the contravariant curl vector is related to the ordinary vector by dividing by the metric component. The speaker emphasizes the importance of careful consideration in promoting quantities to tensors to avoid confusion with additional factors like the square root of the metric determinant.
🎉 Conclusion and Preview of Future Topics
The final paragraph wraps up the discussion on curl in tensor calculus and expresses excitement for upcoming topics. The speaker invites viewers to share their thoughts in the comments and teases future videos on curvature, indicating a shift from purely mathematical discussions to more physical applications of tensor calculus.
Mindmap
Keywords
💡Tensor Calculus
💡Curl
💡Differential Operators
💡Covariant Derivatives
💡Tensor Densities
💡Levi-Civita Symbol
💡Covariant Vectors
💡Contravariant Vectors
💡Spherical Coordinates
💡Metric Tensor
Highlights
Introduction to the episode on tensor calculus for physics, focusing on differential operators, specifically curl.
Explanation of the unique approach to expressing curl in the language of tensors, differing from the book 'Tensor Calculus for Physics' by Dwight E. Newenschwander.
Discussion on the formal treatment of tensor calculus and the special considerations for curl in comparison to divergence and the Laplacian.
Introduction to the concept of tensor density and its distinction from a tensor, with the Levi-Civita symbol as an example.
Explanation of how the determinant of the metric and the Levi-Civita symbol transform as tensor densities.
The importance of the tensor density in the context of integration measures and the transformation to a tensor through integration.
Definition of the contravariant Levi-Civita tensor and its role in making the curl expression generally covariant.
The simplification of the curl expression using the contravariant Levi-Civita tensor and covariant derivatives.
Clarification on the use of covariant and contravariant vectors and derivatives in the curl expression for ease of calculation.
Derivation of the contravariant curl vector component and its relationship to the ordinary vector.
The cancellation of connection coefficients in the curl expression, simplifying the final form.
Application of the curl expression in spherical coordinates as an example to demonstrate the generality of the approach.
Conversion of the covariant vector to the ordinary vector in the context of spherical coordinates.
Final expression for the curl component in spherical coordinates, relating the contravariant vector to the ordinary vector.
Highlighting the practicality of the derived curl expression for use in any coordinate system.
Anticipation for the upcoming videos on curvature, indicating a shift towards more physical applications of tensor calculus.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: