Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams

The Organic Chemistry Tutor
21 Mar 201916:58
EducationalLearning
32 Likes 10 Comments

TLDRThis video explains the concept of probability, focusing on defining key terms like sample space, favorable outcomes, and calculating the probability of various events. It walks through examples of tossing multiple coins, rolling dice, and drawing balls from an urn to demonstrate how to list out sample spaces, determine numbers of favorable outcomes, and divide them by total possible outcomes to calculate probabilities. The video explains that probability ranges from 0 (impossible event) to 1 (certain event) and how to interpret different probability values.

Takeaways
  • 😀 Probability is calculated as number of favorable outcomes divided by total possible outcomes
  • 😊 Sample space represents all possible outcomes that can occur
  • 💡 Probability ranges from 0 (impossible event) to 1 (certain event)
  • 📝 Can use tree diagrams to determine sample space when multiple events occur
  • 🤔 Conditional probability calculates probability of one event given another event occurred
  • 🧮 Contingency tables summarize relationship between two categorical variables
  • 🌳 Mutually exclusive events cannot occur at the same time
  • ⚖️ Independent events have no effect on each other's probabilities
  • 🔢 Complementary events cover all possible outcomes between them
  • 📈 Other relevant probability topics covered in stats playlist
Q & A

  • What is sample space in probability?

    -The sample space is the set of all possible outcomes that can occur in an experiment or random trial.

  • How do you calculate the probability of an event occurring?

    -To calculate the probability of an event occurring, take the number of favorable outcomes that lead to that event and divide it by the total number of possible outcomes.

  • What does a probability value of 0.3 mean?

    -A probability value of 0.3 means there is a 30% chance of that event happening. Out of 10 trials, we would expect the event to occur around 3 times.

  • How do you construct a tree diagram for a probability experiment?

    -To construct a tree diagram, start with the first step of the experiment and draw branches for each possible outcome. Then for each outcome branch, add additional branches for the subsequent step. Continue until all steps are captured.

  • What is meant by 'at least' one head when flipping two coins?

    -When asked for the probability of 'at least one head' when flipping two coins, this includes the outcomes of getting two heads or one head and one tail. It excludes the possibility of getting two tails.

  • What is meant by 'exactly' one tail when flipping three coins?

    -When asked for the probability of 'exactly one tail' when flipping three coins, this means getting outcomes like head-head-tail or head-tail-head. It does not include cases like all heads or all tails.

  • What does 'at most' 4 mean on a die roll?

    -On a die roll, 'at most 4' means the outcomes 1, 2, 3, or 4. It includes getting a 4 but excludes outcomes 5 and 6.

  • What is the difference between sample space and favorable outcomes?

    -The sample space includes all possible outcomes in an experiment. The favorable outcomes are the outcomes within the sample space that lead to the event we want to find the probability of.

  • What is meant by mutually exclusive and complementary events?

    -Mutually exclusive events cannot happen at the same time. Complementary events cover all possibilities between them - one or the other must happen.

  • Where can I find more resources on probability?

    -The video creator has a full probability playlist on their Youtube channel. You can also search Youtube for 'The Organic Chemistry Tutor' and topics like conditional probability.

Outlines
00:00
😀 What is Probability and Sample Space

This paragraph introduces the concept of probability (P(a)) and how to calculate it as the number of favorable outcomes divided by total possible outcomes. It also covers sample space - the set of all possible outcomes for an experiment like flipping coins. A tree diagram is used to list out sample spaces.

05:03
😃 Calculating Probability of Events with Coins

This paragraph works through examples of calculating probability for events like getting at least 1 head when flipping 2 fair coins. It also finds the probability of getting at least 2 tails or exactly 1 tail when flipping 3 fair coins using the sample space and tree diagram.

10:04
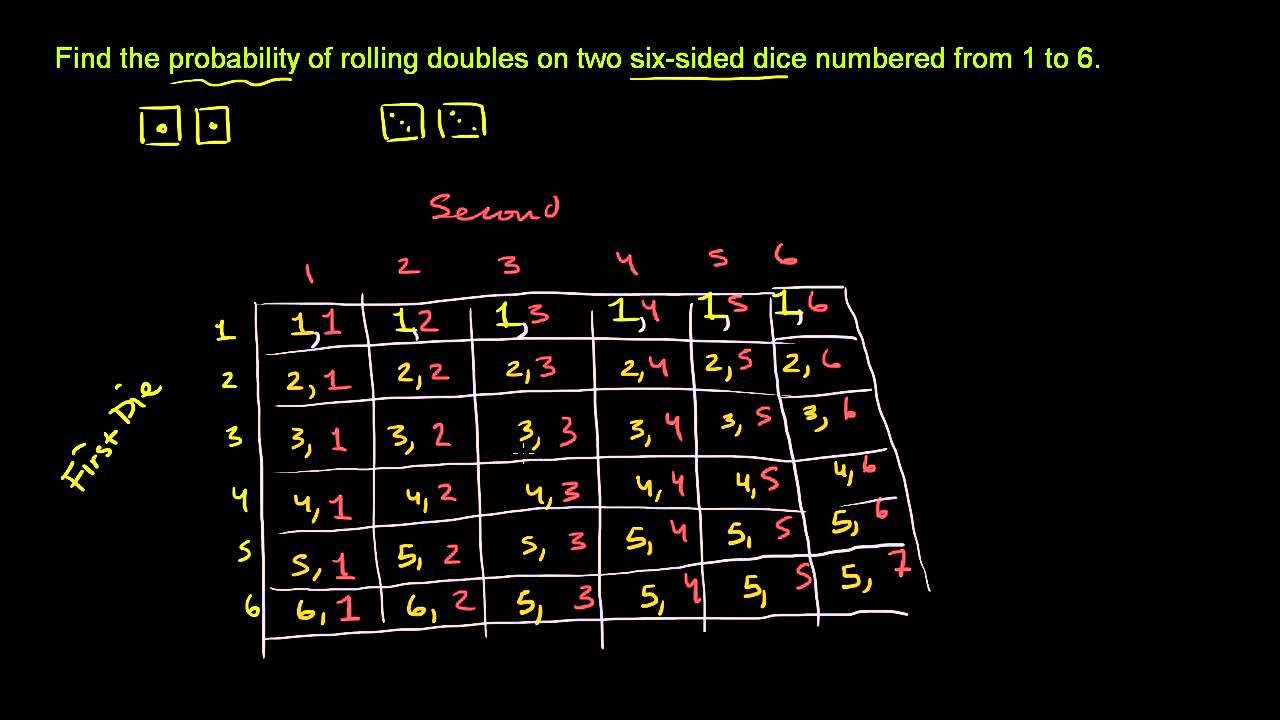
😊 Probability With a 6 Sided Die

This paragraph gives examples of finding probability with a 6 sided die. It covers finding the probability of getting a 2, getting a 3 or 5, getting a number <=4, >3, and <=5. The sample space and favorable outcomes are listed out and used to calculate each probability.

15:05
😀 More Probability and Statistics Videos

The last paragraph let's viewers know there are more probability and statistics videos available. It mentions topics like independent events, conditional probability, contingency tables, etc. and how to access more videos on the channel.

Mindmap
Keywords
💡probability
Probability refers to the likelihood of an event occurring. It is a number between 0 and 1 indicating how likely something is to happen. The video discusses methods to calculate probability, such as finding the number of favorable outcomes divided by total possible outcomes. For example, when flipping two coins the probability of getting at least one heads is 0.75.
💡sample space
The sample space represents all the possible outcomes that can occur in an experiment. For example, when flipping two coins, the sample space is {heads, tails} for each coin, so the overall sample space is {heads, heads}, {heads, tails}, {tails, heads}, {tails, tails}.
💡tree diagram
A tree diagram visually represents the different possible outcomes by branching out different possibilities from an initial starting point. For example, a tree diagram can illustrate all possible outcomes of flipping multiple coins by having each branch represent an additional coin flip.
💡favorable outcome
A favorable outcome is an outcome that leads to the event we are interested in. For example, when calculating probability of getting at least one heads when flipping two coins, the favorable outcomes are {heads, heads}, {heads, tails}, and {tails, heads}.
💡independent events
Independent events are events where the outcome of one event does not affect the outcome of another event. For example, each flip of a coin is independent - getting heads on one flip does not make getting heads on the next flip more or less likely.
💡conditional probability
Conditional probability refers to the probability of an event occurring given that another event has already occurred. For example, the probability that it is raining given that the grass is wet.
💡mutually exclusive
Mutually exclusive events refer to events that cannot happen simultaneously. For example, when rolling a die, getting a 1 and getting a 2 are mutually exclusive.
💡complementary events
Complementary events refer to all outcomes that did not occur in the original event. For example, if event A is getting a 5 when rolling a die, the complementary event is getting 1, 2, 3, 4 or 6.
💡contingency table
A contingency table summarizes the frequency distribution of variables. It is often used in probability to represent the number of times different outcomes occur from an experiment.
💡statistics
Statistics is the study of collecting, analyzing, and making inferences from data. Probability falls under the domain of statistics.
Highlights

Probability is calculated as number of favorable outcomes divided by total possible outcomes

Sample space represents all possible outcomes that can occur

Tree diagrams help determine sample space when multiple events occur

Probability is always between 0 and 1

If probability is 0, event can never happen; if 1, event always happens

Probability of 0.3 means 30% chance of event occurring

Calculate probability by favorable outcomes divided by total outcomes

At least one head when flipping two coins has 75% probability

Getting at least two tails when flipping three coins has 50% probability

Exactly one tail when flipping three coins has 37.5% probability

Numbers less than or equal to 5 with six sided die has 83.3% probability

Check video description for full statistics and probability playlist

Using examples shows how to calculate probability of various events

Calculating probability is straightforward with practice on examples

Understanding sample space is key first step before probability calculations

Transcripts

Browse More Related Video

What is Probability? (GMAT/GRE/CAT/Bank PO/SSC CGL) | Don't Memorise

Chapter 4 Probability Part 1

Probability of More Complex Outcome

4.1.0 Basics of Probability - Lesson Overview, Key Concepts and Learning Outcomes

Die rolling probability | Probability and combinatorics | Precalculus | Khan Academy

Probability of Complementary Events & Sample Space

Rate This

5.0 / 5 (0 votes)

Thanks for rating: