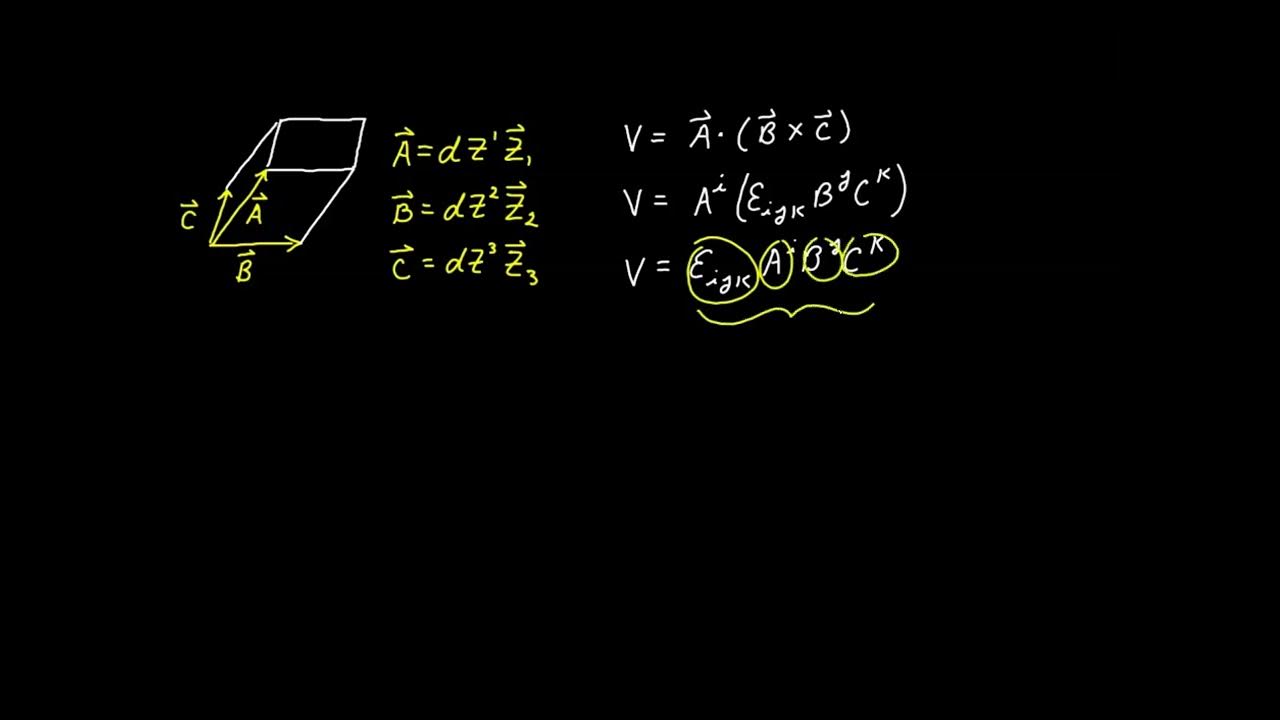Video 48 - Volume Element

Tensor Calculus

6 Sept 202318:43

EducationalLearning

32 Likes 10 Comments

TLDRIn this video, the concept of the volume element in tensor calculus is introduced, which is the square root of the determinant of the covariant metric tensor, denoted as 'Z'. The video demonstrates how the volume element varies across different coordinate systems, such as Cartesian, affine, polar, cylindrical, and spherical, each having a unique expression for 'Z'. It also derives the partial derivative of the volume element with respect to a coordinate variable 'z_i', showing its relationship with the Christoffel symbols. The volume element is highlighted as a crucial tool in tensor calculus, similar to the role of the Jacobian in linear algebra, but with a focus on its positive, non-negative nature.

Takeaways

📚 The video introduces the concept of the volume element in tensor calculus, which is the square root of the determinant of the covariant metric tensor (Z).
🔍 The volume element is not an invariant and varies with different coordinate systems, serving a similar purpose to the Jacobian determinant in linear algebra but always non-negative.
📏 The script explains that the volume element is represented as the absolute value of the Jacobian determinant to ensure it is non-negative, indicating orientation preservation.
📈 The volume element is calculated for various coordinate systems: Cartesian (1), affine (a * b * sin(α)), polar (r), cylindrical polar (ρ), and spherical polar (r² * sin(θ)).
📝 The determinant of the covariant metric tensor is shown to be calculated by multiplying diagonal elements in Cartesian, polar, and cylindrical coordinates, but requires more computation in affine and spherical polar coordinates.
🧩 The video demonstrates the process of deriving the partial derivative of the volume element with respect to a coordinate variable, using the covariant metric tensor and the Christoffel symbols.
🔧 The chain rule is applied to find the partial derivative of the determinant Z, leading to a relationship involving the Christoffel symbols and the metric tensor.
⚖️ The final expression for the partial derivative of the volume element with respect to z_i is given by the volume element multiplied by the Christoffel symbol, indicating how it changes with respect to the coordinate.
🔑 The Christoffel symbols are key in understanding how the volume element transforms between coordinate systems, as shown by the contraction with the metric tensor.
🔄 The script emphasizes the importance of the volume element in tensor calculus for future applications, such as the derivation of the Volterra formula in the next video.
🔑 The video concludes with a brief review, reinforcing the significance of the volume element and its role in tensor calculus, especially in transformations between coordinate systems.

Q & A

What is the new object introduced in video 48 of tensor calculus?
-The new object introduced is the volume element, which is the square root of the determinant of the covariant metric tensor, denoted as Z.
Why is the determinant of a second ranked mixed tensor considered an invariant quantity?
-The determinant of a second ranked mixed tensor is an invariant quantity because it remains unchanged under coordinate transformations, making it an absolute tensor of rank 0.
What is the weight of the determinant of a second ranked tensor with two lower indexes?
-The determinant of a second ranked tensor with two lower indexes is a relative tensor of weight 2 due to the positive exponent of 2 in the transformation factor.
How is the volume element related to the Jacobian determinant in linear algebra?
-The volume element is roughly equivalent to the Jacobian determinant used in linear algebra for changing or transforming from one coordinate system to another, but it is always non-negative.
What is the volume element for Cartesian coordinates?
-In Cartesian coordinates, the volume element is 1, as the determinant of the covariant metric tensor is simply the product of the diagonal elements, which are all 1.
What is the expression for the volume element in affine coordinates?
-The volume element in affine coordinates is given by a * b * sine(Alpha), derived from the determinant of the covariant metric tensor.
How is the volume element calculated for plain polar coordinates?
-In plain polar coordinates, the volume element is r, as the determinant of the covariant metric tensor is r squared, and the square root of that gives r.
What is the volume element for cylindrical polar coordinates?
-For cylindrical polar coordinates, the volume element is rho, since the determinant of the covariant metric tensor is rho squared, and taking the square root yields rho.
What is the expression for the volume element in spherical polar coordinates?
-In spherical polar coordinates, the volume element is r squared * sine(Theta), derived from the determinant of the covariant metric tensor.
What is the derived relationship for the partial derivative of the volume element with respect to a coordinate variable z_i?
-The partial derivative of the volume element with respect to z_i is the volume element itself, times the Christoffel symbol of the second kind, contracted with the covariant metric tensor.

Outlines

00:00

📚 Introduction to the Volume Element in Tensor Calculus

This paragraph introduces the concept of the volume element in tensor calculus, which is the square root of the determinant of the covariant metric tensor. It explains the difference between absolute and relative tensors, emphasizing that the determinant of a second-ranked tensor with two lower indices is a relative tensor of weight 2. The video script discusses the simplification of notation using 'Z' to represent the determinant and 'Z Prime' for its transformed version. It also touches on the role of the volume element, which is analogous to the Jacobian determinant in linear algebra, but with the important distinction that the volume element is always non-negative, representing a positive value or zero.

05:00

📘 Calculating Volume Elements in Different Coordinate Systems

The second paragraph delves into the calculation of the volume element for various coordinate systems, starting with Cartesian coordinates where the determinant is simply 1, leading to a volume element of 1. It then moves on to affine coordinates, where the determinant involves a more complex calculation resulting in a volume element of 'a * b * sine(Alpha)'. The script continues with plain polar, cylindrical polar, and spherical polar coordinates, each with its unique determinant and resulting volume element expressions. For plain polar, the volume element is 'r', for cylindrical it's 'rho', and for spherical it's 'r^2 * sine(Theta)'.

10:00

🔍 Derivation of Partial Derivatives of the Volume Element

This paragraph focuses on the derivation of the partial derivative of the volume element with respect to a coordinate variable. It begins by discussing the determinant of the covariant metric tensor and how it can be broken down using the chain rule. The script introduces a relationship between the cofactor and the determinant, which is then used to simplify the expression for the partial derivative. The process involves contracting both sides of the equation with the contravariant metric tensor and simplifying to find that the partial derivative of 'Z' with respect to 'z_i' is 'Z * gamma^m_i'. The paragraph concludes with the expression for the partial derivative of the volume element itself.

15:00

📝 Summary of the Volume Element and its Partial Derivative

The final paragraph provides a summary of the concepts covered in the video, including the introduction of the volume element and its role in tensor calculus. It reiterates that the volume element is not an invariant object and varies across different coordinate systems. The script also reviews the transformation of the volume element using the absolute value of the Jacobian determinant. The paragraph concludes with the derived relationship for the partial derivative of the volume element with respect to 'z_i', which is expressed as the product of the volume element and the Christoffel symbol. This relationship is highlighted as a key takeaway that will be utilized in future videos, starting with the derivation of the geodesic equation.

Mindmap

Keywords

💡Volume Element

The volume element is a fundamental concept in differential geometry and tensor calculus, representing the volume of an infinitesimal region in a given coordinate system. It is defined as the square root of the determinant of the metric tensor, denoted as √|g| in the script. The volume element is crucial for understanding how volume changes under coordinate transformations and is used in integrals over a manifold. In the video, the volume element is derived for various coordinate systems, such as Cartesian, affine, polar, cylindrical, and spherical, illustrating its role in tensor calculus.

💡Tensor Calculus

Tensor calculus is a mathematical framework for handling tensor operations in a coordinate-free manner, which is essential for general relativity and other areas of physics. It extends the concepts of vectors and scalars to higher dimensions and allows for the manipulation of these quantities under changes of coordinates. The video script discusses the introduction of the volume element within the context of tensor calculus, emphasizing its importance in the field.

💡Covariate Metric Tensor

The covariant metric tensor, often denoted as 'g_ij', is a key component in differential geometry. It encodes the geometry of a space by providing a way to measure distances and angles. In the script, the determinant of the covariant metric tensor is used to define the volume element, highlighting its significance in determining the properties of space in various coordinate systems.

💡Determinant

The determinant is a scalar value that can be computed from a square matrix and is used to describe the volume scaling factor of the linear transformation described by the matrix. In the context of the video, the determinant of the covariant metric tensor is essential for defining the volume element and understanding the geometric properties of different coordinate systems.

💡Jacobian Determinant

The Jacobian determinant is a measure of how a function transforms an infinitesimal region in one coordinate system to another. It is used in various fields, including physics and engineering, to understand changes in variables under transformations. In the script, the Jacobian determinant is compared to the volume element, with the latter being always non-negative, unlike the Jacobian which can be positive or negative depending on the orientation of the coordinate systems.

💡Coordinate Systems

Coordinate systems are used to define positions in a geometric space using a set of numbers. The video script discusses several types of coordinate systems, including Cartesian, affine, polar, cylindrical, and spherical, each with its own properties and applications. The volume element is derived for each of these systems, demonstrating how it varies with the choice of coordinates.

💡Christoffel Symbols

Christoffel symbols, denoted as Γ in the script, are used in differential geometry and general relativity to describe the motion of a vector field along another vector field. They are crucial for understanding how vectors change as one moves through a curved space. In the script, Christoffel symbols are used in the derivation of the partial derivative of the volume element with respect to a coordinate variable.

💡Partial Derivative

A partial derivative is a derivative of a function of multiple variables with respect to one of those variables, while the others are held constant. In the context of the video, the partial derivative of the volume element with respect to a coordinate variable is derived, showing how the volume element changes locally in response to small changes in the coordinate.

💡Orientation

Orientation in a coordinate system refers to the handedness of the system, which can be either right-handed or left-handed. The script mentions that the sign of the Jacobian determinant can indicate the orientation of the coordinate systems involved in a transformation, with positive indicating the same orientation and negative indicating opposite orientations.

💡Invariance

Invariance in physics and mathematics refers to the property of a quantity that remains unchanged under certain transformations. The script discusses how the determinant of a second-rank mixed tensor is an invariant quantity, meaning it has the same value regardless of the coordinate system used, which is a fundamental concept in tensor calculus.

💡Relative Tensor

A relative tensor is a tensor that changes under coordinate transformations in a specific way, as opposed to an absolute tensor, which remains invariant. In the script, the determinant of a second-rank tensor with two lower indices is identified as a relative tensor of weight 2, indicating how it scales under transformations.

Highlights

Introduction of a new object known as the volume element in tensor calculus.

Illustration of the volume element's value in various sample coordinate systems.

Derivation of the partial derivative of the volume element with respect to coordinate value z i.

Explanation of the determinant of a second-ranked mixed tensor as an invariant quantity.

Differentiation between absolute and relative tensors based on the determinant of a second-ranked tensor.

Application of these results to the covariant metric tensor using the letter Z.

Simplification of syntax with the introduction of Z and Z Prime to represent determinants.

Expression of Z Prime in terms of J squared times Z and the introduction of the volume element.

Comparison of the volume element to the Jacobian determinant in linear algebra.

Clarification on the orientation of coordinate systems and its impact on the Jacobian determinant.

Demonstration of the volume element's non-negativity and its role in tensor calculus.

Calculation of the volume element in Cartesian coordinates and its simplification to one.

Determination of the volume element in affine coordinates as a B sine Alpha.

Calculation of the volume element in plain polar coordinates as simply r.

Derivation of the volume element in cylindrical polar coordinates as rho.

Calculation of the volume element in spherical polar coordinates as r squared sine Theta.

Derivation of the partial derivative of the determinant Z with respect to z i using the chain rule.

Use of the cofactor and the contravariant metric tensor to isolate the partial derivative.

Final expression for the partial derivative of the volume element with respect to z i.

Review of the role of the volume element in tensor calculus and its transformation properties.

Anticipation of the use of the derived relationships in future videos, starting with the next one.

Transcripts

Browse More Related Video

Tensor Calculus 5b: Invariants Are Tensors

Video 31 - Christoffel Symbol Examples

Video 50 - Voss Weyl Examples

Video 54 - Integration

Video 42 - Trajectory Examples

Video 12 - Jacobian Examples