Probability Formulas, Symbols & Notations - Marginal, Joint, & Conditional Probabilities
TLDRThe video provides key probability formulas and concepts for students learning the topic. It covers calculating marginal, union, joint, conditional, and negation probabilities. It explains the symbols for union and intersection and how to tell if events are independent, dependent, or mutually exclusive. It discusses the addition rule for 'or' and multiplication rule for 'and.' It also compares the conditional probability and Bayes Theorem formulas. Overall, the video aims to equip students with the main formulas and conceptual understanding needed to solve common probability problems.
Takeaways
- 😀 Marginal probability calculates the chance of a single event occurring independently.
- 📊 Union probability is the chance that either event A or event B occurs.
- 🔀 Joint probability is the chance that both events A and B occur together.
- ❗️ Conditional probability calculates the chance of A given B has already occurred.
- ✅ Independent events do not affect each other's probabilities.
- 🔗 Dependent events have probabilities that rely on prior events.
- ☑️ The addition rule applies when calculating 'A or B'.
- ✖️ The multiplication rule applies when calculating 'A and B'.
- 🔻 Bayes' theorem relates conditional and joint probability.
- ❌ Negation probability is the chance that an event does NOT occur.
Q & A
What is marginal probability?
-Marginal probability is the probability of a single event occurring independent of other events. For example, what is the probability of event A occurring given a sample space of numbers 1-9.
What do the symbols ∪ and ∩ represent?
-The symbol ∪ represents union, combining the elements of two sets. The symbol ∩ represents intersection, finding the common elements between two sets.
How do you calculate union probability?
-Union probability is calculated using the addition rule: P(A or B) = P(A) + P(B) - P(A and B). For mutually exclusive events, P(A and B) = 0.
What is joint probability?
-Joint probability is the probability that both events A and B occur together simultaneously. It's calculated as P(A and B) = P(B|A)P(A) = P(A|B)P(B).
What are some examples of independent vs dependent events?
-Tossing coins and drawing marbles with replacement are independent events. Drawing marbles without replacement are dependent events since the probabilities change based on previous draws.
What does P(A|B) represent?
-P(A|B) represents the conditional probability - the probability of A occurring given that B has already occurred.
How are conditional probability and Bayes theorem related?
-Conditional probability P(A|B) = P(A & B) / P(B). Bayes theorem gives an equivalent form using P(B|A) instead.
When can P(AB) and P(BA) be different?
-P(AB) and P(BA) represent the order of events, with A occurring before B vs B before A. So they can be different if the order matters.
What is negation probability?
-Negation probability is the probability that the complement of an event occurs, equal to 1 - P(A). For example, if P(B) = 0.35, P(not B) = 1 - 0.35 = 0.65.
What key formulas should I memorize for probability?
-Key formulas: marginal probability, addition/multiplication rules, conditional probability, Bayes theorem, joint probability, negation probability. Understand when to apply each one.
Outlines
😀 Introducing Key Probability Concepts and Formulas
The first paragraph introduces key concepts in probability that will be covered in the video, including types of probabilities, symbols and notation, independent and dependent events, mutually exclusive events, and formulas that will be discussed.
😃 Understanding Marginal, Union, and Intersection Probability
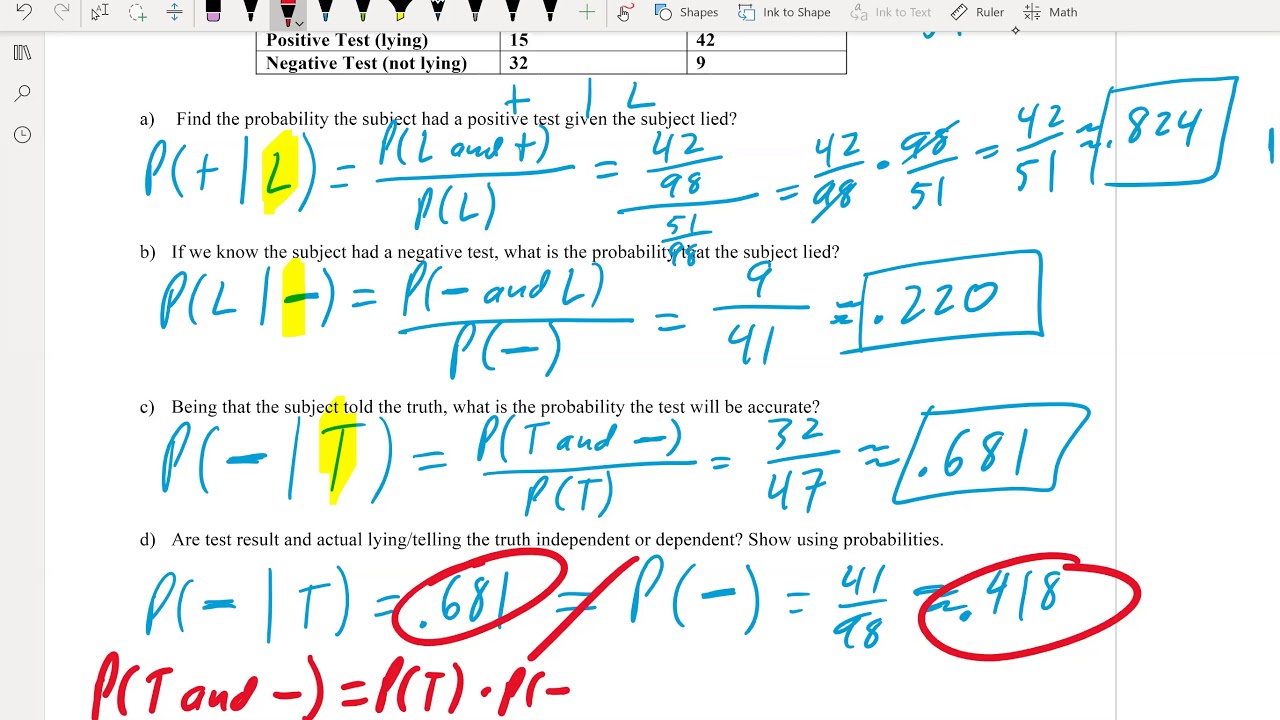
The second paragraph explains marginal, union, and intersection probability using a specific example and numerical sample space. It covers calculating probability for individual events as well as combined events using addition and multiplication rules.
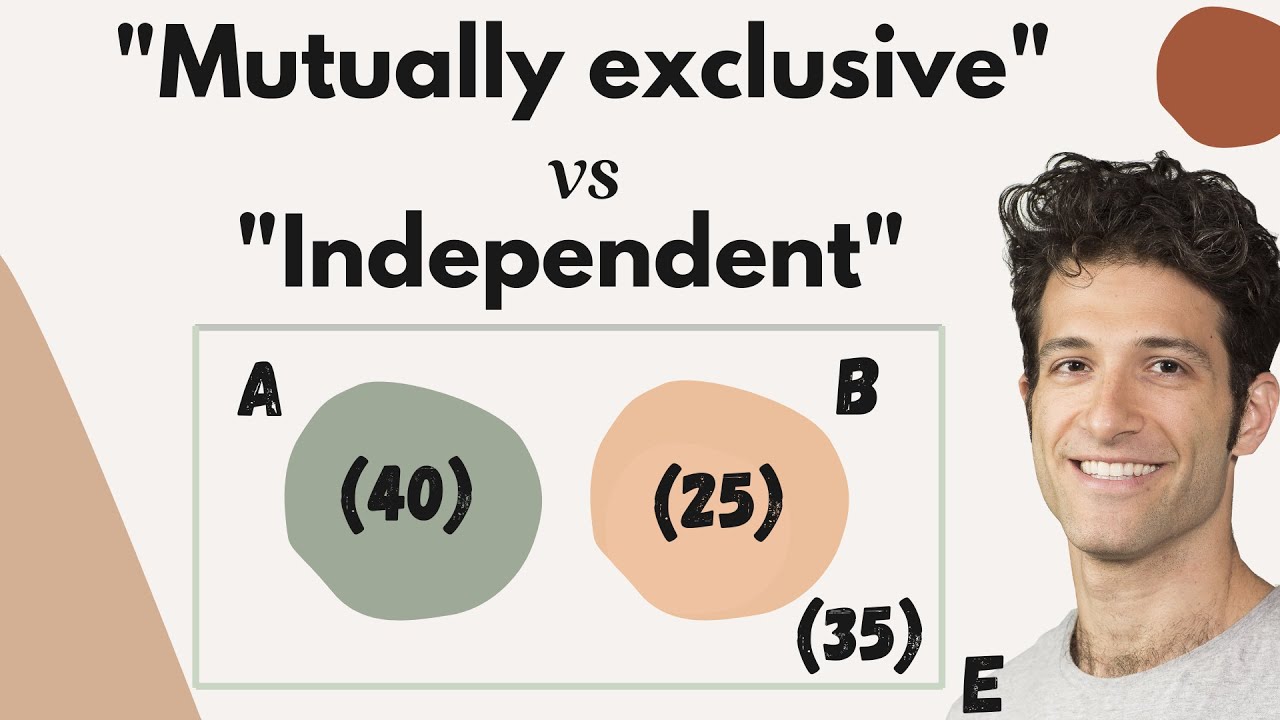
😄 Distinguishing between Mutually Exclusive and Non-Mutually Exclusive Events
The third paragraph explains the difference between mutually exclusive and non-mutually exclusive events, using Venn diagrams to visualize the concepts. It also shows how to calculate joint and union probability for these different types of events.
😁 Calculating Joint, Conditional, and Bayes Theorem Probability
The fourth paragraph covers formulas for calculating joint probability, conditional probability, and Bayes theorem. It explains the multiplication rule for joint probability and the relationship between conditional probability and Bayes theorem.
😆 Independent vs. Dependent Probability Events
The fifth paragraph distinguishes between independent and dependent probability events using examples of drawing marbles and tossing coins. It explains how replacement affects dependency between sequential events.
🤔 Clarifying Order and Simultaneity in Probability Expressions
The sixth paragraph notes that probability expressions may or may not imply order of events, clarifying the potential ambiguity. It recommends specifics like subscripts to denote clear event sequence.
😯 Introducing Conditional Probability and Bayes Theorem
The seventh paragraph formally introduces the concepts of conditional probability and Bayes theorem. It relates them through joint probability and marginal probability formulas.
🥳 Covering Additional Key Probability Concepts
The final paragraph notes coverage of key probability concepts and formulas, inviting viewers to explore additional example problems in linked materials.
Mindmap
Keywords
💡Marginal probability
💡Union probability
💡Joint probability
💡Conditional probability
💡Independent events
💡Dependent events
💡Mutually exclusive
💡Complementary event
💡Multiplication rule
💡Addition rule
Highlights
Marginal probability is the probability of a single event occurring independent of other events.
The probability that an event will occur is equal to the number of successful outcomes divided by the total possible outcomes.
Union probability is the probability that either event A will occur, or event B will occur, or both event A and B will occur.
The addition rule: The probability that event A or event B will occur is equal to the probability of A plus the probability of B minus the probability of A and B occurring together.
Joint probability is the probability that both events A and B will occur together simultaneously at the same time.
For independent events, the joint probability is simply the probability of A times the probability of B.
Conditional probability is the probability of event A occurring given that event B has already occurred.
Conditional probability equals the joint probability divided by the marginal probability.
Bayes' theorem gives another way to calculate conditional probability using probabilities of B given A, A, and B.
The probability that the complement of A will occur is 1 minus the probability that event A will occur.
Mutually exclusive events have zero probability of occurring together.
The word "or" is associated with the addition rule, "and" is associated with the multiplication rule.
Dependent events are when one event affects the probability of the other event occurring.
Order matters when calculating the probability of A then B vs B then A.
Pick the right probability formula based on whether events are occurring together, in sequence, are conditional, etc.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: