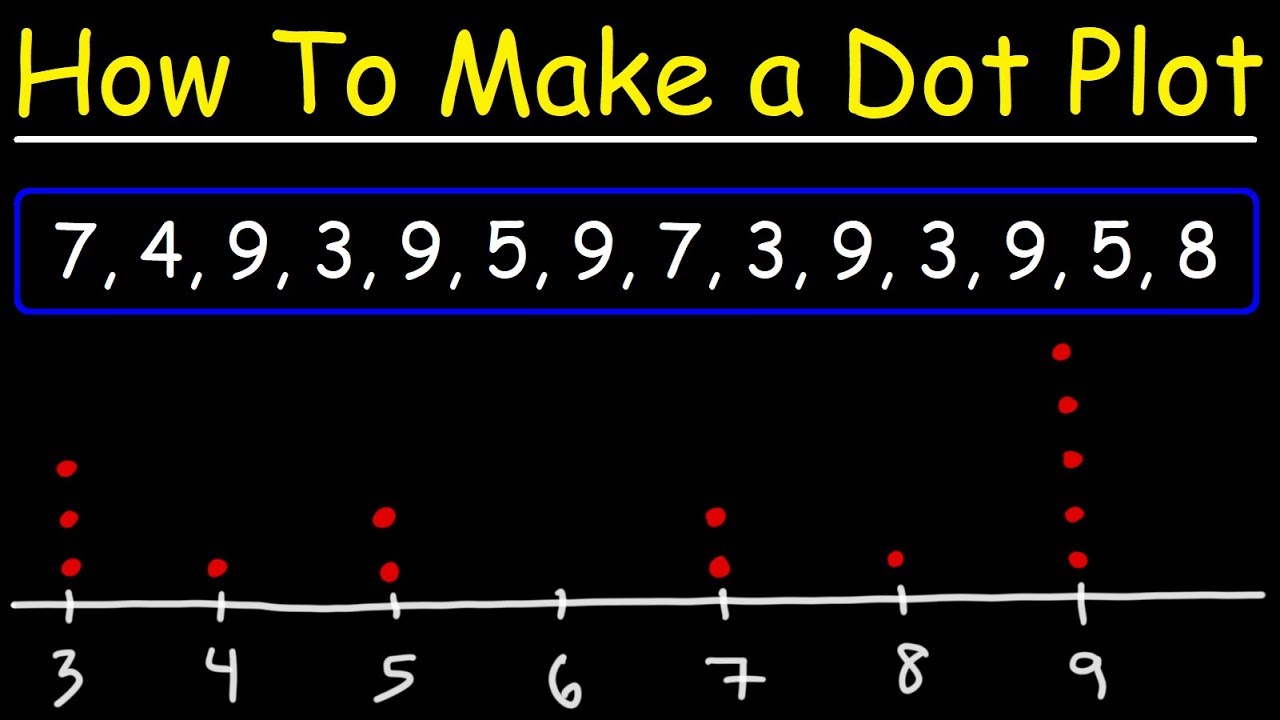
How To Make a Cumulative Relative Frequency Table

The Organic Chemistry Tutor
9 Jan 201905:04
EducationalLearning
32 Likes 10 Comments

TLDRThis video demonstrates how to construct a cumulative relative frequency table using a data set. It first explains creating columns for value, frequency, relative frequency and cumulative relative frequency. It then tallies the values' frequencies, sums them to get the total frequency, and divides individual frequencies by the total to calculate relative frequencies. After verifying relative frequencies sum to 1, it cumulatively adds them to populate the last column. Finally, it emphasizes the utility of these tables and reminds viewers to subscribe.

Takeaways
  • 😀 We are going to make a cumulative relative frequency table using provided data
  • 👍🏻 The table will have 4 columns: Value, Frequency, Relative Frequency, and Cumulative Relative Frequency
  • 📝 We count the frequency for each unique data value
  • 🔢 We calculate the total frequency by summing the Frequency column
  • 🧮 Relative Frequency is calculated by Frequency divided by Total Frequency
  • 🔄 We verify Relative Frequencies sum to 1 before continuing
  • ↗️ Cumulative Relative Frequency starts with the Relative Frequency
  • ↗️ Then each next Cumulative Relative Frequency adds the previous Relative Frequency
  • 📈 The final Cumulative Relative Frequency reaches 1.0 when complete
  • 👋 Don't forget to subscribe and thanks for watching the video
Q & A

  • What are the four columns created in the frequency table?

    -The four columns created are: V for value, F for frequency, RF for relative frequency, and CRF for cumulative relative frequency.

  • How many total data values are there in the data set?

    -There are a total of 25 data values in the data set.

  • What is the frequency of the number 3 in the data set?

    -The frequency of the number 3 is 8.

  • What is the relative frequency of the number 5?

    -The relative frequency of the number 5 is 0.16.

  • What is the purpose of taking the sum of the relative frequency column?

    -Taking the sum verifies that the relative frequencies add up to 1, which they should.

  • How is cumulative relative frequency calculated?

    -Cumulative relative frequency is calculated by adding the current relative frequency to the previous cumulative relative frequency.

  • Why create a cumulative relative frequency table?

    -A cumulative relative frequency table allows you to see the cumulative distribution of the data, not just the individual frequencies.

  • What is the cumulative relative frequency for the number 8?

    -The cumulative relative frequency for the number 8 is 0.88.

  • What is the purpose of this video?

    -The purpose is to demonstrate the process of creating a cumulative relative frequency table from a data set.

  • What is the final cumulative relative frequency value and what does it represent?

    -The final cumulative relative frequency value is 1.0. This represents 100% of the data set.

Outlines
00:00
😄 Creating a Cumulative Relative Frequency Table

The paragraph explains the step-by-step process of creating a cumulative relative frequency table using a given data set. It goes through calculating the frequencies, relative frequencies, and cumulative relative frequencies for each value in the data. Key steps include determining the frequency counts, summing the frequencies, calculating relative frequencies by dividing frequencies by the total, ensuring relative frequencies sum to 1, and calculating cumulative relative frequencies by adding up the previous relative frequencies.

Mindmap
Keywords
💡frequency
The frequency refers to the number of times a particular data value occurs in the dataset. It is important for understanding the distribution of values. For example, the transcript calculates the frequency of the number 2 being 5, as there are 5 occurrences of 2 in the dataset.
💡relative frequency
The relative frequency is the frequency of a data value divided by the total number of data values. It shows the proportion of times that value occurs. For example, the relative frequency of 2 is 5/25 = 0.2, meaning 2 makes up 20% of the dataset.
💡cumulative relative frequency
The cumulative relative frequency is the sum of the relative frequencies so far. It shows the proportion of values less than or equal to that value. For example, the cumulative relative frequency of 6 is 0.8, meaning 80% of the dataset consists of values less than or equal to 6.
💡table
The key output of the video is a frequency distribution table summarizing the dataset. This table has columns showing the distinct data values, frequencies, relative frequencies, and cumulative relative frequencies.
💡distribution
The frequency table shows the distribution of values in the dataset - how they are spread out and their proportions. Analyzing this distribution is key for statistics.
💡calculate
The transcript goes through the calculations involved in getting the frequencies, relative frequencies and cumulative relative frequencies for all values in the dataset.
💡proportion
Relative frequency represents the proportion of times each value occurs in the dataset out of the total values.
💡sum
Finding the total frequency involves summing the individual frequencies. Summing the relative frequencies checks that together they equal 1.
💡value
The values refer to the distinct numbers or data points present in the dataset being analyzed.
💡frequency distribution
The end result table showing frequencies of each data value is referred to as a frequency distribution. It summarizes the occurrence of different values.
Highlights

We're going to focus on making a cumulative relative frequency table using the data

The first column will be for the data values, the second for frequencies, the third for relative frequencies, and the last for cumulative relative frequencies

We count the occurrences of each data value to populate the frequency column

We take the sum of the frequencies as the total frequency needed to calculate relative frequencies

Relative frequency is calculated by dividing each frequency by the total frequency

We check that the relative frequencies sum to 1 before continuing

Cumulative relative frequency starts with the first relative frequency value

Each cumulative relative frequency adds the next relative frequency value

The final cumulative relative frequency should equal 1

This table allows us to analyze the distribution and cumulative distribution of the data

It's helpful for statistical analysis like finding percentiles

Great for visualizing the proportion of data below or above thresholds

Important for probability and sampling applications

Useful precursor to more advanced statistical approaches

Consider graphing distributions or relationships once table is built

Transcripts

Browse More Related Video

How To Make a Relative Frequency Distribution Table

Elementary Statistics - Chapter 2 - Exploring Data with Tables & Graphs

Mean, Median, and Mode of Grouped Data & Frequency Distribution Tables Statistics

Elementary Stats Lesson #3 A

Dot Plots and Frequency Tables

Introduction to Statistics

Rate This

5.0 / 5 (0 votes)

Thanks for rating: