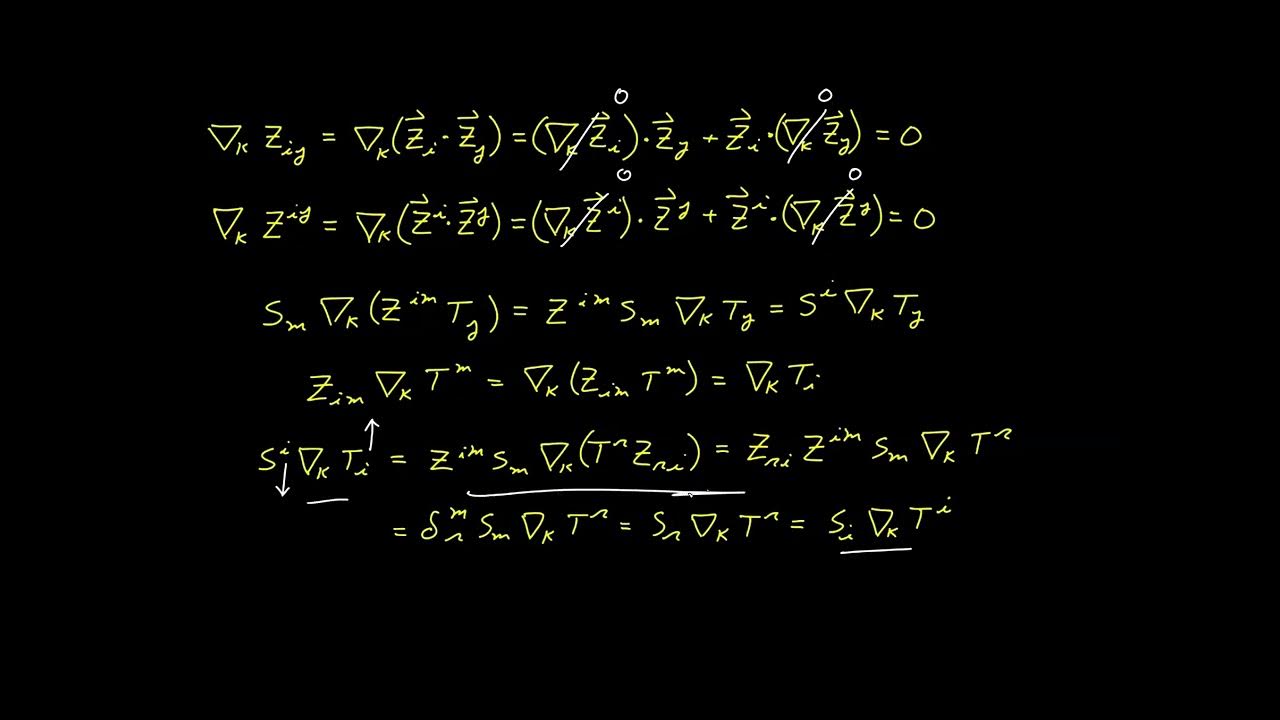Tensor Calculus For Physics Ep. 12: Christoffel Symbols
TLDRIn this educational video, the presenter revisits the concept of tensors, focusing on the covariant derivative and its transformation properties. They explain the necessity of the covariant derivative for tensor calculus, introducing the affine connection coefficients and their symmetrical properties under index exchange, crucial for defining torsion-free space. The presenter then introduces the Christoffel symbols, derived from the metric tensor, to uniquely determine these coefficients. The video concludes with a discussion on metric compatibility and its implications for tensor calculus, setting the stage for future topics like divergence, curl, and the Riemann curvature tensor.
Takeaways
- 🔍 The script is a continuation of a series on tensor calculus, focusing on the covariant derivative and its role in ensuring tensors transform properly under coordinate changes.
- 📚 The covariant derivative is defined with the addition of an affine connection, which is necessary for the derivative of a tensor to still be a tensor.
- 🔧 The affine connection coefficients, which are symmetric under the exchange of the bottom two indices due to the no-torsion condition, are crucial for the covariant derivative.
- 📉 The main goal of the video is to introduce the Christoffel symbols, which are a unique set of connection coefficients derived from additional requirements imposed on the system.
- 📝 The covariant derivative of a second-rank tensor is explained, with specific attention to the signs associated with contravariant and covariant indices.
- 🧩 Metric compatibility is introduced as a key requirement, stating that the covariant derivative of the metric tensor should be zero, implying that the dot product of basis vectors remains unchanged under parallel transport.
- 🔑 The process of deriving the Christoffel symbols involves taking the covariant derivative of the metric tensor in three different permutations and setting up an equation to solve for the connection coefficients.
- ⚖️ The Christoffel symbols are uniquely determined by the metric tensor through a specific formula involving partial derivatives and the inverse metric tensor.
- 🌐 The script clarifies that nonzero Christoffel symbols do not necessarily imply curvature of space; they are related to the change in basis vectors, even in flat spaces.
- 📚 The upcoming videos will cover complex differential operations on tensors, such as divergence, curl, and laplacian, in the context of covariant derivatives.
- 🔮 The video concludes with a teaser for future content, hinting at the development of a formalism for determining space curvature and the introduction of the Riemann curvature tensor.
Q & A
What is the covariant derivative and why is it important in tensor calculus?
-The covariant derivative is a modification of the standard derivative that ensures the resulting object still transforms as a tensor under coordinate transformations. It is important because it allows for the differentiation of tensors in a way that maintains their tensorial properties, which is crucial for tensor calculus in curved spaces.
What are the conditions for the connection coefficients to be symmetric under the exchange of the bottom two indices?
-The connection coefficients are symmetric under the exchange of the bottom two indices when there is no torsion present. This condition is known as the norm torsion rule and it significantly reduces the number of possible sets of connection coefficients.
What is the significance of the Christoffel symbols in the context of the video script?
-Christoffel symbols are unique sets of connection coefficients that are defined in terms of the metric tensor. They are crucial for taking covariant derivatives of tensors and are used to impose the condition of metric compatibility.
What does metric compatibility mean and why is it imposed?
-Metric compatibility is the condition that the covariant derivative of the metric tensor should be equal to zero. It is imposed because it ensures that the dot product of basis vectors remains unchanged under parallel transport, which is a desirable property in the context of differential geometry.
How is the covariant derivative of a second-rank tensor different from that of a vector?
-The covariant derivative of a second-rank tensor involves additional terms with connection coefficients for each index of the tensor. The sign of these terms depends on whether the index is contravariant (positive) or covariant (negative).
What is the process of deriving the Christoffel symbols from the condition of metric compatibility?
-The process involves taking the covariant derivative of the metric tensor three times, each time with a different permutation of indices, and then setting the results equal to zero. By taking the difference of these equations, one can solve for the Christoffel symbols using the metric tensor and its inverse.
Why are the Christoffel symbols of the second kind different from the first kind?
-The Christoffel symbols of the second kind are defined without lowering any indices, while the first kind involves lowering the lambda index. This difference in index positioning leads to different expressions for the two types of Christoffel symbols.
How do the Christoffel symbols relate to the concept of curvature in space?
-While Christoffel symbols are often associated with curvature, they do not directly indicate whether space is curved. They are connection coefficients that describe how basis vectors change as one moves through space, which can be nonzero even in flat space when using non-Cartesian coordinates.
What are the implications of nonzero Christoffel symbols in flat space?
-In flat space, nonzero Christoffel symbols indicate that the basis vectors change with position, even though the underlying geometry of the space remains unchanged. This is a characteristic of non-Cartesian coordinate systems, such as spherical coordinates.
What will be the focus of the next video after the one described in the script?
-The next video will focus on more complex differential operations acting on tensors, such as divergence, curl, and laplacian, in the context of covariant derivatives. This will be followed by an introduction to the Riemann curvature tensor in subsequent videos.
Outlines
📚 Introduction to Tensor Calculus and Covariant Derivatives
This paragraph introduces the concept of tensor calculus, specifically focusing on the covariant derivative. The speaker explains that while the derivative of a tensor does not generally transform as a tensor, adding an additional linear transformation based on the affine connection coefficients allows the result to maintain tensor properties. The covariant derivative is defined, and it's noted that while the transformation is known, the actual coefficients are not yet determined. The lack of torsion is highlighted, which implies symmetry in the connection coefficients, but still leaves many possibilities. The goal is set to impose further requirements to identify a unique set of connection coefficients, known as Christoffel symbols.
🔍 Deriving Christoffel Symbols through Metric Compatibility
The paragraph delves into the process of deriving the unique set of connection coefficients, or Christoffel symbols, by imposing the condition of metric compatibility. This condition states that the covariant derivative of the metric tensor should equal zero, which is interpreted as the dot product of basis vectors remaining unchanged during parallel transport. The process involves taking the covariant derivative of a second-rank tensor with respect to the metric tensor and applying the rule that connection coefficients carry a positive or negative sign depending on whether the index is contravariant or covariant. The paragraph outlines the algebraic manipulations needed to isolate and solve for the Christoffel symbols.
📘 Calculation of Christoffel Symbols Using Inverse Metric
The speaker continues the explanation by detailing the calculation of Christoffel symbols, utilizing the inverse metric to simplify the expressions. The process involves moving terms around and factoring out common elements to isolate the connection coefficients. The resulting formula for the Christoffel symbols is presented, highlighting the relationship between these coefficients and the metric tensor. The distinction between Christoffel symbols of the first and second kind is mentioned, with the current focus being on the second kind.
🌐 Christoffel Symbols, Curvature, and Upcoming Topics
In the final paragraph, the speaker clarifies misconceptions about Christoffel symbols being directly associated with space curvature, emphasizing that nonzero symbols do not necessarily imply a curved space. The role of Christoffel symbols in different coordinate systems, such as Cartesian and spherical, is discussed, showing how they capture the change in basis vectors. The speaker previews upcoming topics, including complex differential operations on tensors, divergence, curl, Laplacian, and the introduction of the Riemann curvature tensor in future videos.
Mindmap
Keywords
💡Tensor
💡Covariant Derivative
💡Affine Connection Coefficients
💡Torsion
💡Christoffel Symbols
💡Metric Tensor
💡Metric Compatibility
💡Second-Rank Tensor
💡Inverse Metric
💡Riemann Curvature Tensor
Highlights
Introduction to the concept of tensor time and the covariant derivative.
Explanation of how the covariant derivative ensures tensor transformation properties are maintained.
Discussion on the lack of unique connection coefficients without additional constraints.
Imposition of no torsion condition leading to symmetric connection coefficients.
Introduction of the goal to define unique connection coefficients known as Christoffel symbols.
Differentiation between covariant derivatives of vectors and second-rank tensors.
Description of the metric compatibility requirement for the covariant derivative of the metric tensor.
Presentation of the method to uniquely solve for connection coefficients using metric compatibility.
Derivation of the Christoffel symbols of the second kind from the metric tensor.
Misunderstanding clarified regarding the relationship between Christoffel symbols and space curvature.
Explanation of how Christoffel symbols capture the change in basis vectors in different coordinate systems.
Differentiation between Christoffel symbols of the first and second kind.
Discussion on the implications of Christoffel symbols for divergence, curl, and laplacian in various coordinate systems.
Clarification that nonzero Christoffel symbols do not necessarily indicate curved space.
Example given of how Christoffel symbols behave in Cartesian and spherical coordinates.
Anticipation of future videos discussing complex differential operations and the Riemann curvature tensor.
Conclusion summarizing the video's content and预告of upcoming topics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: