Tensor Calculus 25 - Geometric Meaning Ricci Tensor/Scalar (Volume Form)
TLDRThis video delves into the geometrical implications of the Ricci curvature tensor and scalar, building upon the concept of sectional curvature introduced in a previous video. It explains how the Ricci tensor measures volume changes along geodesics, utilizing both an orthonormal basis approach and a new method involving the volume element derivative. The video also corrects a mistake regarding dimensionality in a previous example and explores the relationship between the Ricci scalar, volume deviation in curved spaces, and the algebraic properties of these tensors.
Takeaways
- 📚 The script continues a discussion on the geometrical meanings of the Ricci curvature tensor and the Ricci scalar, building on a previous video's introduction to sectional curvature and its implications on geodesic behavior.
- 🔍 It corrects a mistake from a previous video regarding the dimensionality of a ball used to illustrate changes in volume due to Ricci curvature, emphasizing the importance of using a two-dimensional disc for such examples.
- 📏 The Ricci tensor is explored through a new approach involving the volume element derivative, applicable in any basis, not just orthonormal ones.
- 📐 The volume form, denoted by the lowercase Omega symbol, is introduced as a tensor that quantifies the volume enclosed by a set of vectors, with its numerical output determined by the determinant of a matrix formed by the vectors' components in an orthonormal basis.
- 🧩 The concept of the Levi-Civita symbol is explained as a tool for calculating the volume of parallelograms formed by vectors, with its properties and use in summations to find determinants highlighted.
- 🔄 The script explains how to calculate the volume enclosed by vectors in non-orthonormal bases by involving the determinant of the forward matrix or the square root of the metric tensor matrix determinant.
- 🌐 The covariant derivative of the volume form is shown to be zero, indicating that the rules for measuring volumes remain consistent along geodesics, despite actual volumes potentially changing.
- 📈 The Ricci tensor is derived from the second covariant derivative of the volume form, revealing how it quantifies the rate of volume change due to spatial curvature along geodesics.
- 🔢 The Ricci scalar is discussed as a scalar obtained from the summation of the Ricci tensor, indicating how the volume of a ball in curved space deviates from that in flat space.
- 🌍 The video concludes with a detailed example of how the Ricci scalar relates to the surface area of a sphere compared to a flat disk, illustrating the impact of positive curvature on volume measurements.
- 📚 The script promises further exploration of the algebraic properties of the Ricci tensor and scalar in a subsequent video, hinting at a deeper dive into their mathematical characteristics and implications.
Q & A
What is the Ricci curvature tensor and what does it measure?
-The Ricci curvature tensor is a measure of the curvature of space that quantifies how volumes change as they move along geodesics. It sums up the sectional curvatures in every direction of an orthonormal basis, providing an overall sense of how volumes expand or contract due to the space's curvature.
What is the relationship between sectional curvature and Ricci curvature?
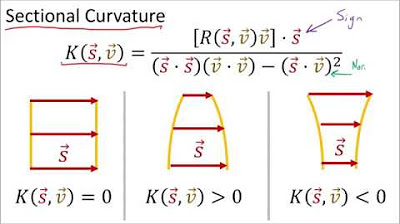
-Sectional curvature measures how neighboring geodesics converge or diverge due to the curvature of space. The Ricci curvature is the sum of all sectional curvatures in every direction of an orthonormal basis, giving a comprehensive measure of volume change.
How is the Ricci tensor related to the volume change of a ball moving along geodesics?
-The Ricci tensor indicates how the volume of a ball changes as it moves along geodesics in a curved space. A positive Ricci curvature implies that volumes tend to shrink, while a negative Ricci curvature suggests that volumes tend to expand.
What is the volume form and how is it used to calculate volumes in different bases?
-The volume form, denoted by the lowercase Omega symbol, is a tensor that gives the volume enclosed by a set of vectors. It is calculated by taking the determinant of the matrix with the components of each vector arranged in columns in an orthonormal basis. For non-orthonormal bases, the volume form is given by the square root of the determinant of the metric tensor times the Levi-Civita symbol.
What is the significance of the covariant derivative of the volume form being zero?
-The covariant derivative of the volume form being zero signifies that the rules for measuring volumes do not change along geodesics, even though the volumes themselves may change due to the curvature of space.
How does the Ricci tensor arise from considering the volume element derivative?
-The Ricci tensor arises from taking two covariant derivatives of the volume form along a geodesic path. This approach to the Ricci tensor works in any basis and leads to the understanding that the Ricci tensor measures how volumes change due to the curvature of space.
What is the Ricci scalar and how does it relate to the volume of a ball in curved space?
-The Ricci scalar is a scalar obtained by summing over the Ricci tensor with one upper index and one lower index. It indicates how much the size of a ball in curved space deviates from the standard volume of a ball in flat space, given the same radius.
What is the significance of the Ricci scalar being positive or negative in the context of space curvature?
-A positive Ricci scalar indicates that the space has a tendency for volumes to be smaller than expected for a given radius, as seen on a sphere. Conversely, a negative Ricci scalar suggests that volumes are larger than expected for the same radius, which could be the case in negatively curved spaces.
How does the Ricci tensor differ from the sectional curvature in terms of measuring the effects of space curvature?
-While sectional curvature measures the convergence or divergence of neighboring geodesics in a specific plane, the Ricci tensor provides a more comprehensive measure of how volumes change as they move along geodesics in all directions of space.
What is the connection between the Ricci tensor and the metric tensor in the context of volume change?
-The components of the volume form tensor, which is used to calculate volumes in different bases, include the square root of the determinant of the metric tensor matrix. This connection shows that the metric tensor plays a crucial role in understanding how volumes change in different coordinate systems.
Outlines
📚 Introduction to Ricci Curvature and Scalar
This paragraph introduces the concepts of Ricci curvature and Ricci scalar, continuing from a previous video. It discusses the sectional curvature and how it measures the convergence or divergence of geodesics due to space curvature. The Ricci curvature is defined as the sum of sectional curvatures in an orthonormal basis, and it's related to the volume change of a ball moving along geodesics. The presenter corrects a previous mistake regarding the dimensionality of a ball in a curvature example and emphasizes that the Ricci curvature tracks changes in the size of a ball as it travels along geodesics. A new approach to understanding the Ricci tensor through the volume element derivative is introduced, applicable in any basis, not just orthonormal.
📐 Understanding the Volume Element and its Derivative
The paragraph delves into the concept of the volume element, denoted by the lowercase Omega symbol, which is a tensor representing the volume enclosed by a set of vectors. It explains how to calculate the two- and three-dimensional volume using the volume form and the determinant of a matrix formed by the components of vectors in an orthonormal basis. The use of the Levi-Civita symbol is introduced for a more compact representation of the volume calculation. The paragraph also discusses how to handle non-orthonormal bases by involving the determinant of the forward matrix or the Jacobian in the calculation. The importance of the metric tensor and its relation to the volume change when changing bases is highlighted.
🔍 Exploring the Covariant Derivative of the Volume Form
The focus shifts to the covariant derivative of the volume form and its implications for volume changes along geodesics. It is shown that the covariant derivative of the volume form is zero, indicating that the rules for measuring volumes remain constant along geodesics, even though the volumes themselves can change. The paragraph explains the process of parallel transporting vectors along a geodesic path and how this affects the volume enclosed by these vectors. The multi-linearity properties of tensors are used to prove that the covariant derivative of the volume form equals zero, which is a key result leading to the introduction of the Ricci tensor.
🌐 Ricci Tensor and Volume Change in Curvature Space
This paragraph explores the relationship between the Ricci tensor and how it quantifies volume changes due to space curvature. It describes the process of taking two covariant derivatives of an arbitrary volume spanned by vectors, which leads to the Ricci tensor. The paragraph explains how separation vectors, representing the distance between neighboring geodesics, are used in this process. The second derivative of the volume is shown to contain a term proportional to the original volume, with the Ricci curvature as the constant of proportionality. This term distinguishes volume changes due to curvature from those that can occur in flat space due to geodesic alignment.
📘 Ricci Scalar and Deviation of Volume from Flat Space
The paragraph introduces the Ricci scalar, which is derived from the Ricci tensor and provides information about how the volume of a ball in curved space deviates from that in flat space. It discusses the concept of comparing volumes by radius and explains how the surface area of a bowl shape on a sphere differs from that of a flat circle. The Taylor series expansion is used to illustrate the relationship between the areas of these shapes, with the Ricci scalar appearing in the second-order term. The implications of positive and negative Ricci scalar values on the volume of a ball are explained, with examples of how the volume can either increase or decrease depending on the curvature.
🔑 Conclusions and Further Exploration of Ricci Properties
The final paragraph summarizes the two main interpretations of the Ricci tensor: one based on sectional curvature and the other on the derivative of the volume form. It emphasizes that the Ricci tensor measures volume changes along geodesics due to curvature and does not provide information about shape changes. The Ricci scalar is again highlighted as an indicator of how volume deviates from the flat space expectation for a given radius. The paragraph concludes with a mention of future content on the algebraic properties of the Ricci tensor and scalar, inviting viewers to look forward to the next video in the series.
Mindmap
Keywords
💡Ricci curvature tensor
💡Ricci scalar
💡Sectional curvature
💡Geodesics
💡Orthonormal basis
💡Volume element
💡Levi-Civita symbol
💡Covariant derivative
💡Metric tensor
💡Riemann curvature tensor
Highlights
The video continues the discussion on the geometrical meanings of the Ricci curvature tensor and the Ricci scalar, building upon the concepts introduced in the previous video.
Sectional curvature, which measures how neighboring geodesics converge or diverge due to space curvature, is explained using an orthonormal basis.
The Ricci curvature is defined as the sum of all scalar curvatures in every basis vector direction, indicating volume change as a ball moves along geodesics.
A correction is made regarding the dimensionality of a ball in the context of Ricci curvature, emphasizing the importance of using a two-dimensional ball for accurate representation.
A new approach to understanding the Ricci tensor is introduced, which involves considering the volume element derivative and works in any basis, not just orthonormal.
The volume element, or volume form, is described as a tensor that gives the volume enclosed by a set of vectors, with a focus on its numerical output.
The concept of the volume form is explored through orthonormal basis vectors, which always form a box with volume one.
The volume form's numerical output is explained using the determinant of a matrix formed by vector components in an orthonormal basis.
The use of the Levi-Civita symbol in calculating the volume of parallelograms formed by vectors is discussed, providing a compact way to compute determinants.
The method of changing basis and its implications on volume calculation, using the forward matrix or Jacobian determinant, is explained.
The relationship between the determinant of the metric tensor and the volume change when changing basis is established.
The volume form tensor's components in a non-orthonormal basis are derived, incorporating the square root of the metric tensor determinant.
The covariant derivative of the volume form is shown to be zero, indicating that the rules for measuring volumes remain constant along geodesics.
The second derivative of the volume along a geodesic path is explored, revealing its relationship with the Ricci tensor and volume change due to curvature.
The Ricci tensor is interpreted as indicating how volumes change in size as they move along geodesics in space, specifically due to curvature.
The Ricci scalar is discussed as a measure of how the volume of a ball in curved space deviates from that in flat space, with implications for understanding space curvature.
The video concludes with a summary of the two interpretations of the Ricci tensor and the significance of the Ricci scalar in understanding space curvature's impact on volume.
Transcripts
Browse More Related Video
Tensor Calculus 24: Ricci Tensor Geometric Meaning (Sectional Curvature)
Tensor Calculus 26 - Ricci Tensor/Scalar Properties
Video 87 - Ricci & Einstein Tensors
Tensor Calculus 23: Riemann Curvature Tensor Components and Symmetries
Video 81 - Intrinsic Curvature
Tensor Calculus 19: Covariant Derivative (Intrinsic) and Geodesics
5.0 / 5 (0 votes)
Thanks for rating: