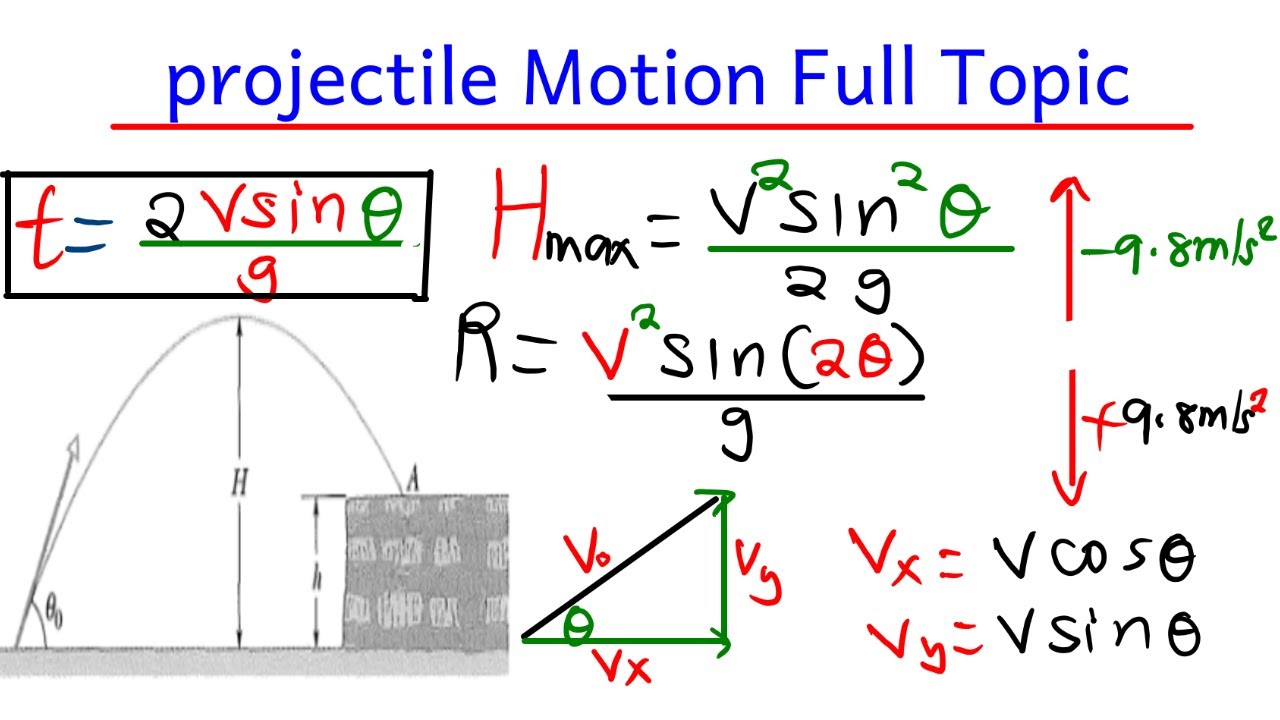
Kinematic Equations 2D
TLDRIn this engaging lecture, Professor Anderson introduces the concept of two-dimensional motion, focusing on projectile motion as exemplified by throwing an object horizontally from the Empire State Building. He explains the parabolic trajectory resulting from gravity and the absence of acceleration in the horizontal direction, leading to the equation for vertical displacement. The lecture culminates in a practical application, calculating the time it takes for an object to fall from a height, using the Empire State Building as a case study.
Takeaways
- 📚 The lecture introduces two-dimensional motion, building upon one-dimensional motion concepts.
- 🎯 Two-dimensional problems are common in physics, despite our three-dimensional world.
- 🏙️ A thought experiment involving throwing a marble from the Empire State Building is used to illustrate projectile motion.
- 🏹 Projectile motion results in a parabolic trajectory due to the influence of gravity.
- 🌐 The only acceleration in projectile motion is in the vertical direction (due to gravity), with no acceleration in the horizontal direction if air resistance is ignored.
- 📈 The kinematic equations can be adapted to solve for vertical displacement over time in projectile motion by substituting 'y' for 'x'.
- 🕒 The time an object spends in the air can be calculated using the formula: T = √(2H/G), where H is the height and G is the acceleration due to gravity.
- 📊 The Empire State Building's height is approximated to 400 meters for the purpose of calculation.
- 🔢 The calculated time for an object to fall from the Empire State Building is approximately 9 seconds.
- 📚 The concept of free fall motion is introduced, which occurs when an object is solely under the influence of gravity.
- 🚀 The vertical component of the initial velocity is zero in the case of horizontal projectile motion.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is two-dimensional motion, specifically focusing on projectile motion and its characteristics.
Why is the motion of an object thrown from a height considered two-dimensional?
-The motion is considered two-dimensional because the object moves along the horizontal (X) axis and the vertical (Y) axis, with no movement towards or away from the observer along the Z axis.
What is the trajectory of a horizontally launched object?
-The trajectory of a horizontally launched object is a parabola.
What force is responsible for the curved trajectory of a projectile?
-Gravity is responsible for the curved trajectory of a projectile, pulling it downwards towards the Earth.
What is the acceleration due to gravity?
-The acceleration due to gravity is approximately -9.8 meters per second squared.
What is the initial vertical velocity (VY initial) of an object launched horizontally?
-The initial vertical velocity (VY initial) of an object launched horizontally is zero.
What is the formula used to calculate the time of flight for a projectile?
-The formula used to calculate the time of flight for a projectile is T = sqrt((2 * H) / G), where H is the initial height and G is the acceleration due to gravity.
How long would it take for an object to fall from the height of the Empire State Building?
-It would take approximately 9 seconds for an object to fall from the height of the Empire State Building, assuming a height of about 400 meters.
Does the time of flight change if the object is dropped vertically instead of being launched horizontally?
-No, the time of flight does not change if the object is dropped vertically instead of being launched horizontally, as the formula only depends on the initial height.
What is the significance of understanding projectile motion in physics?
-Understanding projectile motion is significant in physics because it governs the motion of many objects moving near the Earth's surface and is a fundamental concept in analyzing real-world problems involving motion.
How does air resistance affect the analysis of projectile motion?
-In the provided script, air resistance is ignored for simplicity. However, in reality, air resistance can affect the trajectory and time of flight of a projectile, making the analysis more complex.
Outlines
📚 Introduction to Two-Dimensional Motion
Professor Anderson begins the lecture by discussing the transition from one-dimensional to two-dimensional motion, emphasizing the relevance of 2D problems in physics. He introduces the concept of projectile motion using the example of throwing an object from the Empire State Building, highlighting that the motion is two-dimensional as it involves X and Y positions without a Z component. The professor explains the parabolic trajectory of the projectile and attributes this curvature to the force of gravity, which acts vertically. He clarifies that in the absence of air resistance, there is no acceleration in the horizontal direction, leading to the concept of free fall motion.
🧮 Kinematic Equations for Projectile Motion
The professor delves into the kinematic equations, focusing on their application to the vertical component of projectile motion. He modifies the standard kinematic equations to reflect the Y-axis (vertical) motion and uses this to calculate the time an object remains in the air. By setting the final Y position (y_final) to zero (ground level) and considering the initial vertical velocity (VY_initial) to be zero for horizontal launch, he simplifies the equation to focus on the acceleration due to gravity (G) and the height (H) from which the object is launched. The resulting equation allows for the calculation of the time of flight (T) for any object falling from a given height under the influence of gravity alone.
🕒 Calculation of Time of Flight for the Empire State Building
The lecture concludes with a practical application of the derived equation to estimate the time it takes for an object to fall from the Empire State Building. The professor approximates the height of the building to 400 meters and applies the formula for time of flight, yielding a result of approximately 9 seconds. This real-world example illustrates the practical use of the kinematic equations for understanding projectile motion and provides a clear conclusion to the lecture on two-dimensional motion.
Mindmap
Keywords
💡Two-dimensional motion
💡Kinematic equations
💡Projectile motion
💡Acceleration due to gravity
💡Free fall motion
💡Coordinate system
💡Trajectory
💡Horizontal launch
💡Time of flight
💡Empire State Building
Highlights
Introduction to two-dimensional motion and its relevance in physics.
Kinematic equations' applicability to one-dimensional motion and the desire to extend these concepts to two dimensions.
The transition from one-dimensional to two-dimensional problems, emphasizing the commonality in physics problems.
Illustrative example of throwing a marble off the Empire State Building to discuss projectile motion.
Explanation of the parabolic trajectory resulting from horizontal projectile motion.
The concept of projectile motion and its relation to free fall motion.
The role of gravity in causing the object's trajectory to curve downward.
The absence of acceleration in the horizontal direction due to the lack of horizontal force.
The kinematic equation tailored for vertical motion in the context of projectile motion.
Derivation of the time of flight for an object in projectile motion using the derived kinematic equation.
The independence of time of flight on initial vertical velocity when launched horizontally.
The calculation of time of flight for an object falling from a height, specifically referencing the Empire State Building.
Conversion of the Empire State Building's height from feet to meters for calculation purposes.
The application of the derived formula to calculate the approximate time of flight for the marble.
The conclusion that the marble would be in the air for approximately nine seconds.
The encouragement for further questions and clarification through office hours.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: