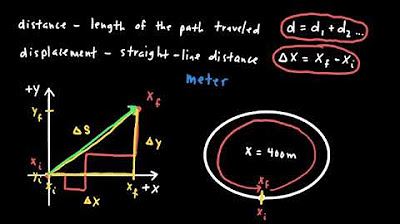
Kinematics Part 1: Horizontal Motion

Professor Dave Explains
26 Jan 201706:37
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Professor Dave delves into the fundamentals of classical physics, focusing on mechanics, which分为 kinematics and dynamics. Kinematics, developed by Galileo, deals with motion without considering forces, while dynamics examines the effects of forces on motion. The video introduces three core kinematic equations that relate velocity, position, and acceleration to time, and provides examples of their application in real-world scenarios, such as calculating a car's velocity and distance traveled with constant acceleration, and determining braking distance during deceleration.

Takeaways
  • 📚 Mechanics is divided into kinematics and dynamics, focusing on describing and explaining the motion of objects without and with forces, respectively.
  • 🌟 Galileo's contributions in the early 1600s were pivotal in developing kinematics, which studies motion without reference to forces.
  • 🚀 Kinematic equations are revolutionary because they apply to all objects, both terrestrial and celestial, despite the need for approximations on Earth due to variables like friction and air resistance.
  • 📈 The fundamental kinematic equations involve variables for displacement, velocity, acceleration, and time, with constant acceleration in the context of kinematics.
  • 🛣️ The first kinematic equation relates velocity at any time to initial velocity, acceleration, and time.
  • 📍 The second equation describes the position of an object as a function of initial position, initial velocity, acceleration, and time.
  • 🔢 The third equation relates the square of velocity to initial velocity, acceleration, and displacement.
  • 🚗 Supplemental equations help derive position as average velocity times time and define average velocity as the average of initial and final velocities.
  • 📊 Applying these equations to real-world scenarios, like driving a car with constant acceleration, allows for practical calculations of velocity and distance traveled.
  • 🚦 When considering sudden stops or changes in motion, such as braking, the kinematic equations can be used to calculate the time taken and distance traveled during the change.
  • 🎓 Understanding and applying these kinematic principles is essential for comprehending the motion of objects in both one and two dimensions.
Q & A

  • What are the two main branches of mechanics in classical physics?

    -The two main branches of mechanics in classical physics are kinematics and dynamics.

  • Who largely developed the field of kinematics?

    -The field of kinematics was largely developed by Galileo in the early 1600s.

  • What does kinematics deal with?

    -Kinematics deals with equations that describe the motion of objects without reference to any kind of forces.

  • How does the study of dynamics differ from kinematics?

    -Dynamics is the study of the effect that forces have on the motion of objects, unlike kinematics which does not consider forces.

  • What are the variables included in kinematic equations?

    -The kinematic equations include variables for displacement, velocity, acceleration, and time.

  • What is the significance of the kinematic equations?

    -The kinematic equations are significant because they revolutionized the understanding that mathematics could describe the motion of all objects, whether on earth or in space, despite the presence of variables like friction and atmosphere.

  • What is the first fundamental kinematic equation?

    -The first fundamental kinematic equation states that the velocity of an object at any time T is equal to the initial velocity plus the acceleration times time.

  • How can you calculate the velocity of a car after 10 seconds with a constant acceleration of 2.5 m/s²?

    -You can calculate the velocity by multiplying the acceleration (2.5 m/s²) by the time (10 seconds), resulting in a velocity of 25 m/s.

  • What is the second fundamental kinematic equation?

    -The second fundamental kinematic equation says that the position of an object with respect to a point of origin will be equal to its initial position plus the initial velocity times time plus one-half the acceleration times time squared.

  • How can you find out how far a car will travel in 10 seconds with an initial velocity of 0 and an acceleration of 2.5 m/s²?

    -You can use the second fundamental kinematic equation, ignoring the initial velocity term, and calculate one-half times the acceleration (2.5 m/s²) times the time squared (10s²), resulting in a distance of 125 meters.

  • What is the third fundamental kinematic equation?

    -The third fundamental kinematic equation states that the velocity squared is equal to the initial velocity squared plus twice the acceleration times the displacement.

  • How long will it take for a car moving at 27 m/s to come to a stop with a deceleration of -8.4 m/s²?

    -To find the time, you can use the first fundamental kinematic equation with a final velocity of 0, an initial velocity of 27 m/s, and an acceleration of -8.4 m/s², which results in a stopping time of 3.2 seconds.

  • What is the relationship between position and average velocity?

    -Position is equal to the average velocity times the time interval, and the average velocity is equal to the final velocity plus the initial velocity divided by 2.

Outlines
00:00
📚 Introduction to Kinematics and Dynamics

This paragraph introduces the audience to the field of mechanics, a major branch of physics, and further divides it into kinematics and dynamics. Kinematics, developed by Galileo, focuses on describing the motion of objects without considering external forces, while dynamics examines the impact of forces on motion. The paragraph emphasizes the revolutionary nature of these concepts, which apply universally, regardless of the object's location. It outlines the fundamental kinematic equations involving displacement, velocity, acceleration, and time, and explains the significance of initial conditions. The paragraph sets the stage for upcoming tutorials that will delve into the application of these equations.

05:02
🚗 Applying Kinematic Equations to Real-World Motion

In this paragraph, the professor illustrates the practical application of kinematic equations to real-world scenarios involving cars. It provides examples of calculating velocity and distance traveled with constant acceleration, as well as the time and distance required to stop a moving car with a given deceleration. The paragraph demonstrates how to use the equations to solve for unknown variables, such as velocity after a certain time or the distance traveled during braking. It emphasizes the versatility of these equations for analyzing motion in various contexts.

Mindmap
Keywords
💡Classical Physics
Classical physics is a branch of physics that deals with the mechanics of everyday objects and the forces that act upon them. It is foundational to the understanding of physical phenomena and is distinct from quantum physics and relativity. In the video, classical physics serves as the basis for the discussion on mechanics, which is divided into kinematics and dynamics, highlighting the historical development and importance of these fields.
💡Mechanics
Mechanics is a branch of physics that studies the motion of objects and the forces that cause these motions. It is divided into kinematics, which describes motion without reference to forces, and dynamics, which examines the effects of forces on motion. Mechanics is crucial for predicting and understanding the behavior of objects in motion, from cars on Earth to celestial bodies in space.
💡Kinematics
Kinematics is the study of motion that does not consider the forces causing the motion. It focuses on describing the motion of objects using quantities such as displacement, velocity, and acceleration without reference to the causes of these changes. Kinematics is essential for developing equations that describe the behavior of objects in motion, regardless of the forces involved.
💡Dynamics
Dynamics is the subfield of mechanics that studies the effects of forces on the motion of objects. It involves understanding how forces cause changes in an object's velocity, acceleration, and direction. Dynamics is crucial for predicting how objects will move when subjected to various forces, such as friction, gravity, and applied forces.
💡Galileo
Galileo Galilei was a pioneering scientist who made significant contributions to the development of kinematics in the early 1600s. His work laid the foundation for the modern understanding of motion and the scientific method. In the context of the video, Galileo's role in the advancement of kinematics is highlighted, emphasizing the historical importance of his contributions to physics.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that describes how quickly an object speeds up, slows down, or changes direction. In kinematics, acceleration is considered constant, simplifying the equations used to predict and analyze motion.
💡Displacement
Displacement is the change in position of an object, usually represented as a vector from the initial position to the final position. It is different from distance traveled, as it takes into account the direction of motion. Displacement is a fundamental concept in kinematics, used to describe the overall motion of an object from one point to another.
💡Velocity
Velocity is the speed of an object in a specified direction. It is a vector quantity that describes both how fast an object is moving and the direction of its motion. In the context of the video, velocity is a key variable in the kinematic equations, used to analyze the motion of objects over time.
💡Kinematic Equations
Kinematic equations are mathematical formulas that relate displacement, velocity, acceleration, and time for an object in motion. These equations are essential tools for analyzing and predicting the motion of objects without considering the forces acting on them. They are derived from the principles of kinematics and are widely used in physics to solve problems involving motion.
💡Initial Conditions
Initial conditions are the values of variables at the starting point of a process or experiment. In kinematics, initial conditions refer to the initial position, velocity, and acceleration of an object. These values are crucial for solving kinematic problems, as they establish the baseline from which changes in motion are measured.
💡Aristotle
Aristotle was an ancient Greek philosopher whose views on natural philosophy, including the motion of objects, influenced scientific thought for centuries. He believed that heavier objects naturally fell faster than lighter ones, which was later disproven by Galileo and others. In the video, Aristotle's views are contrasted with the advancements in understanding motion that occurred with the development of kinematics and dynamics.
💡Friction
Friction is a force that opposes the relative motion or tendency of such motion of two surfaces in contact. It plays a significant role in the dynamics of objects, as it can cause objects to slow down, stop, or even prevent motion from starting. In the context of the video, friction is mentioned as one of the variables that affect motion on Earth, necessitating approximations in the kinematic equations.
Highlights

Introduction to classical physics with a focus on mechanics.

Mechanics is divided into kinematics and dynamics.

Kinematics, developed by Galileo, describes motion without reference to forces.

Dynamics studies the effect of forces on motion.

The revolutionary idea that mathematics can describe the motion of all objects, regardless of their location.

Kinematic equations include variables for displacement, velocity, acceleration, and time.

In kinematics, acceleration has a constant value.

The three fundamental kinematic equations are introduced.

Supplemental equations derived from simple definitions.

Practical application of kinematic equations to real-world examples, such as driving to the supermarket.

Calculating velocity after constant acceleration over time.

Determining the distance traveled with given initial conditions and acceleration.

Example of a car in motion requiring sudden deceleration to stop.

Using kinematic equations to solve for time and distance in braking scenarios.

The universal applicability of kinematic equations to any object, not just cars.

The importance of understanding the equations and variables for solving motion problems.

Encouragement for viewers to subscribe for more tutorials and support the content creator.

Transcripts

Browse More Related Video

2.2 Kinematics in One Dimension | General Physics

AP Physics 1 | Unit 1: Kinematics

Chapter 2 - Motion Along a Straight Line

How to Cram Kinematics in 1 hour for AP Physics 1

2022 Live Review 1 | AP Physics C: Mechanics | One- and Two-Dimensional Kinematics

AP Physics 1 Kinematics Review

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics TutorialClassical MechanicsKinematicsDynamicsGalileo's LegacyMotion EquationsCar AccelerationBraking DistanceAristotle vs. GalileoFriction & Atmosphere