Calculus - Position Average Velocity Acceleration - Distance & Displacement - Derivatives & Limits
TLDRThis video delves into the concepts of calculus as it relates to an object's position, velocity, and acceleration. It explains how to determine an object's direction of motion (right or left), its state (at rest or moving), and its rate of speed change (accelerating or decelerating). The video uses the position function to illustrate how to calculate distance and displacement, and differentiates between the two. It further clarifies the relationship between velocity (a vector) and speed (a scalar), and how to calculate both average and instantaneous velocity and acceleration. The video provides a comprehensive understanding of these principles with examples and emphasizes the importance of recognizing when an object is speeding up, slowing down, or changing direction.
Takeaways
- 📍 The position function (s(t)) represents an object's location over time and can be used to calculate distance and displacement.
- 📈 Distance is a scalar quantity that represents the total path length traveled by an object, always positive, while displacement can be positive or negative, depending on direction.
- 🏃 Velocity is the rate of change of position with respect to time, and it is a vector quantity that considers both speed and direction.
- 🔄 Average velocity is calculated as the net displacement divided by the total time, whereas average speed is the total distance divided by the total time.
- 🚀 Instantaneous velocity is the velocity at a specific time and can be found by taking the first derivative of the position function.
- 🎓 The slope of the tangent line to the position graph at a given time represents the instantaneous velocity.
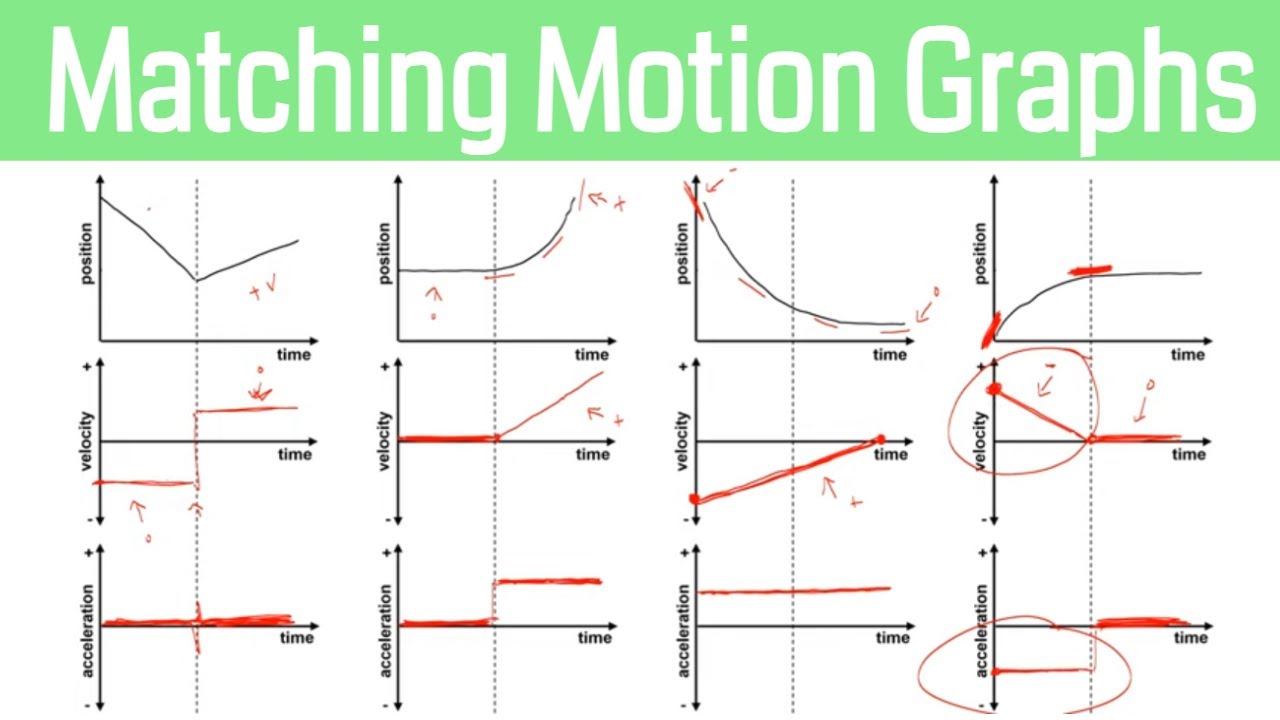
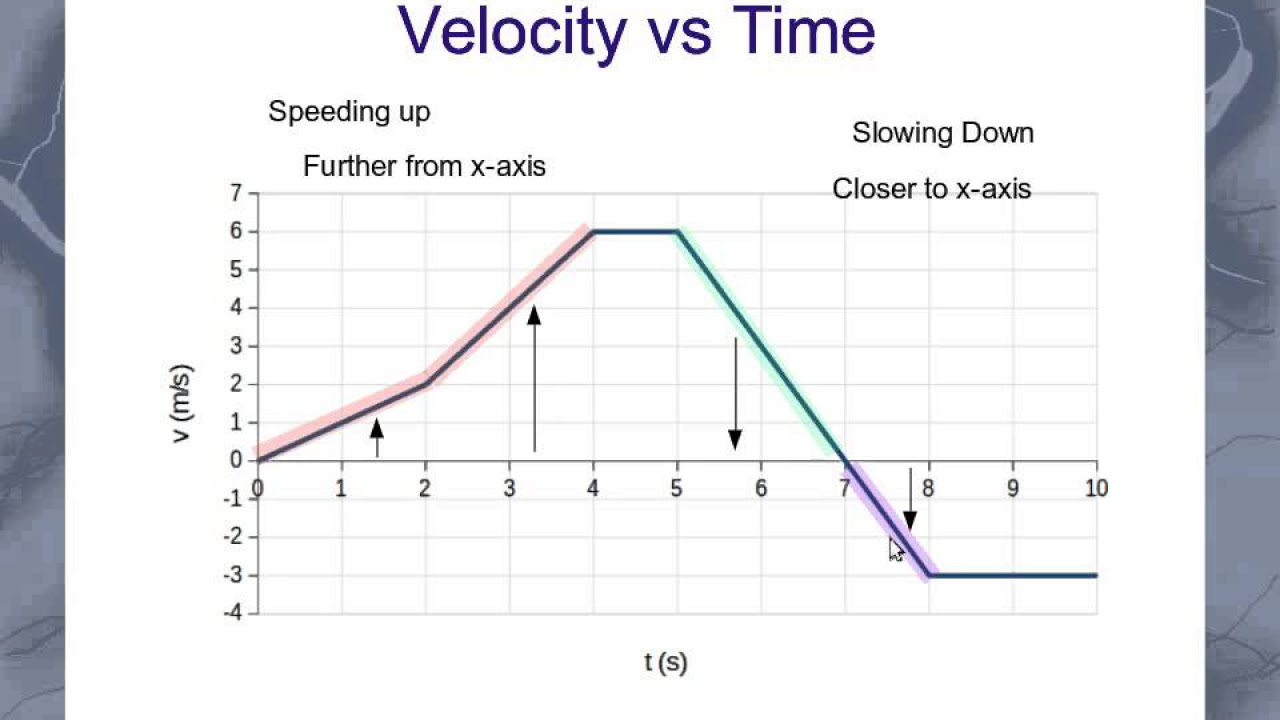
- 🔄 When velocity and acceleration have the same sign, the object is speeding up; when they have opposite signs, the object is slowing down.
- 📊 To estimate instantaneous velocity or acceleration from a data table, use the average velocity or acceleration between two points centered around the time of interest.
- 🤔 At times when velocity is zero, the object could be at rest or changing direction; acceleration can help determine the situation.
- 📌 The total distance traveled by an object is the sum of the absolute values of the distances covered in each segment of its path.
- 📐 Calculus concepts like limits and derivatives are essential for understanding and calculating velocity and acceleration from a position function.
Q & A
What does the position function (s(t)) represent in calculus?
-The position function (s(t)) represents the location of an object at a given time. It can indicate the object's position on the x-axis, y-axis, or in an x-y coordinate system. Using the position function, one can calculate distance, displacement, and other related quantities.
How do you calculate the total distance traveled by an object?
-To calculate the total distance traveled by an object, you sum up the absolute values of all the individual distances covered, regardless of direction. Distance is a scalar quantity and is always positive.
What is the difference between distance and displacement?
-Distance is the total length of the path traveled by an object, regardless of direction, and is always a positive scalar quantity. Displacement, on the other hand, is the straight-line distance between the starting and ending points, including the direction, and can be positive or negative depending on the direction of movement.
How is velocity related to displacement and time?
-Velocity is the rate of change of displacement with respect to time. It is a vector quantity that considers both the magnitude and direction of an object's movement. Average velocity is calculated as the net displacement divided by the total time, while instantaneous velocity is the velocity at a specific moment in time.
What is the relationship between velocity and the derivative of the position function?
-The derivative of the position function (s(t)) with respect to time represents the instantaneous velocity of the object. In other words, the velocity function (v(t)) is the first derivative of the position function (s(t)).
How can you determine if an object is moving to the right, left, or is at rest?
-An object is moving to the right if its velocity is positive, moving to the left if its velocity is negative, and at rest if its velocity is zero. However, a velocity of zero does not necessarily mean the object is at rest; it could also indicate a momentary change in direction.
What is acceleration, and how is it related to velocity and velocity change?
-Acceleration is the rate of change of velocity with respect to time. It indicates how quickly the velocity of an object is increasing or decreasing. Positive acceleration means the velocity is increasing, while negative acceleration means the velocity is decreasing. If acceleration and velocity have the same sign, the object is speeding up; if they have opposite signs, the object is slowing down.
How do you calculate the average acceleration between two points?
-To calculate the average acceleration between two points, you use the change in velocity (final velocity minus initial velocity) divided by the time interval between those two points. This gives you the average rate of change of velocity over the specified time period.
How can you approximate the instantaneous velocity at a specific time using a data table?
-If you have a data table with time and position values, you can approximate the instantaneous velocity at a specific time by finding the average velocity over two points that bracket the time of interest, using the midpoint of those two times as the approximation for the instantaneous velocity.
What is the displacement of an object in the first five seconds according to the given position function?
-The displacement of the object in the first five seconds, according to the position function s(t) = t^3 - 6t^2 + 9t + 1, is 20 units (from position 1 at t=0 to position 21 at t=5).
How do you find the total distance traveled by an object in the first five seconds?
-To find the total distance traveled in the first five seconds, you sum up the individual distances traveled during each time interval, considering the direction of movement. In this case, the object traveled 4 units to the right in the first second, 4 units to the left in the next two seconds, and then 20 units to the right in the last two seconds, resulting in a total distance of 28 units.
Outlines
📚 Introduction to Calculus and Position, Velocity, and Acceleration
This paragraph introduces the concepts of calculus as it relates to position, velocity, and acceleration. It discusses how to determine the direction of a particle's movement (right or left) and its state (at rest, speeding up, or slowing down). The position function is explained, highlighting its role in calculating location on the x-axis or y-axis and in determining distance and displacement. The distinction between distance (scalar) and displacement (vector) is clarified, with examples illustrating how to calculate total distance and net displacement.
🏃♂️ Understanding Velocity and Instantaneous Velocity
The paragraph delves into the calculation of velocity, which is associated with speed, and how it is derived from the position function. It differentiates between average velocity and instantaneous velocity, with the latter being the slope of the tangent line on the position graph. The concept of using secant lines to approximate the slope of the tangent line is introduced, along with the mathematical representation of instantaneous velocity as the first derivative of the position function.
🔄 Determining Direction and State of Motion
This section explains how to determine if a particle is moving to the right or left and whether it is at rest, speeding up, or slowing down. It clarifies that a zero velocity does not necessarily mean the particle is at rest, as it could be changing direction. The relationship between velocity, acceleration, and speed is discussed, with emphasis on the signs of these quantities to understand the motion's direction and state.
📈 Calculating Velocity and Acceleration from Position Function
The paragraph focuses on deriving the velocity function from a given position function and understanding its implications. It involves finding the instantaneous velocity by differentiating the position function and discussing the significance of the velocity function's shape in understanding the motion's dynamics. The paragraph also introduces the concept of acceleration as the derivative of the velocity function, which indicates how velocity changes over time.
🤔 Estimating Instantaneous Velocity and Speed
This section discusses the methods for estimating the instantaneous velocity and speed at a specific time using average velocity. It explains how to choose appropriate points to approximate the instantaneous velocity and how to calculate the instantaneous speed, which is always positive. The paragraph also addresses the importance of understanding the difference between velocity (which includes direction) and speed (which does not).
📊 Interpreting Velocity and Acceleration Graphs
The paragraph explains how to interpret velocity and acceleration graphs to determine the motion of a particle. It describes how to identify intervals where the particle is moving to the right or left, at rest, speeding up, or slowing down by analyzing the signs of velocity and acceleration. The concept of combining velocity and acceleration information to understand the particle's motion is emphasized, along with the notation used to represent intervals of motion.
🌟 Understanding Speed and Constant Motion
This section clarifies the concepts of speeding up and slowing down in relation to the signs of velocity and acceleration. It explains why a particle speeds up when these quantities have the same sign and slows down when they have opposite signs. The paragraph also discusses the conditions under which a particle moves with constant speed and the implications of zero acceleration on the velocity's constancy.
📝 Calculating Displacement and Total Distance
The paragraph outlines the methods for calculating displacement and total distance traveled by a particle. It provides a step-by-step explanation of how to find the displacement during the first five seconds using the position function and how to calculate the total distance by summing the absolute values of displacements. The process of determining the points of direction change and using them to calculate total distance is also discussed.
🔢 Working with Data Tables for Velocity and Acceleration
This section discusses how to work with data tables to calculate average velocity and acceleration. It explains the formulas for calculating average velocity and acceleration using changes in position and velocity over time intervals. The paragraph also covers the estimation of instantaneous velocity and acceleration at specific times using average values between data points.
📚 Using Limits to Calculate Velocity and Acceleration
The paragraph explains the use of limits to calculate the velocity function from a position function and to find the velocity at a specific point. It details the process of differentiating the position function using the limit definition of the derivative. The alternative form of the derivative is also introduced for finding the instantaneous velocity at a particular time point. The paragraph concludes with a comprehensive example demonstrating the application of these concepts.
Mindmap
Keywords
💡Calculus
💡Position Function (s(t))
💡Velocity
💡Acceleration
💡Displacement
💡Distance
💡Instantaneous Velocity
💡Average Velocity
💡Instantaneous Acceleration
💡Average Acceleration
Highlights
The video discusses the concepts of calculus as it relates to position, velocity, and acceleration, providing insights into how these quantities can be used to determine an object's motion.
The position function (s(t)) is introduced as a way to determine an object's location on the x-axis or y-axis, and it can be used to calculate distance and displacement.
Distance is a scalar quantity that represents the total path length traveled by an object, while displacement is a vector quantity that considers direction.
Velocity is defined as the rate of change of position with respect to time and is a vector quantity that accounts for both speed and direction.
Average velocity is calculated as the net displacement divided by the total time, whereas average speed is the total distance divided by the total time.
Instantaneous velocity can be found by taking the first derivative of the position function, which gives the velocity function (v(t)).
The sign of the velocity indicates the direction of motion: positive for rightward movement and negative for leftward movement.
Acceleration is the rate of change of velocity with respect to time, and it can be used to determine if an object is speeding up or slowing down.
An object is considered to be speeding up when the acceleration and velocity have the same sign, and slowing down when they have opposite signs.
The video provides a method for calculating the instantaneous acceleration at a specific time using the limit process and the definition of the derivative.
A detailed example is given to demonstrate how to find the instantaneous velocity and acceleration for a given position function.
The video explains how to use a data table to approximate the instantaneous velocity and acceleration when the explicit function is not provided.
The concept of total distance traveled versus net displacement is clarified, with examples showing how to calculate both quantities.
The video concludes with a comprehensive example that ties together the concepts of position, velocity, and acceleration to analyze an object's motion over a given time interval.
The importance of understanding the relationship between velocity, acceleration, and the direction of motion is emphasized for solving problems in calculus.
The video provides a clear and detailed explanation of how to determine when a particle is at rest, moving to the right, or moving to the left using calculus.
The role of calculus in analyzing motion, including the ability to determine rest, direction, speed, and acceleration, is demonstrated through the use of mathematical functions and derivatives.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: