Unit VII: Lec 3 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis lecture delves into the concept of 'Absolute Convergence' in series, contrasting it with 'Conditional Convergence'. It explains that while a series with alternating signs can converge, the sum can change with the order of terms, a phenomenon not present in finite arithmetic. The series 1 - 1/2 + 1/3 - 1/4 + ... is used as an example to illustrate convergence and the importance of term order. The lecturer emphasizes the stability of absolutely convergent series, where rearranging terms does not affect the sum, and warns against altering the order in conditionally convergent series.
Takeaways
- 📚 The lecture introduces the concept of 'Absolute Convergence' in series where terms are not all positive.
- 🔍 It's explained that a series can converge even if its terms are not all positive, with the series 1 - 1/2 + 1/3 - 1/4 + ... serving as an example.
- 🔢 The n-th term of the series is represented as (-1)^(n+1) / n, showcasing how terms alternate in sign and decrease in magnitude.
- 📉 The importance of the n-th term approaching zero for convergence is reiterated, though it's noted this alone isn't sufficient for convergence.
- 📈 The lecture demonstrates the convergence of the alternating series geometrically, using partial sums to show the series approaches a limit.
- 🌐 It's revealed that the sum of the series 1 - 1/2 + 1/3 - 1/4 + ... is actually the natural logarithm of 2, ln(2).
- 🚫 The series is conditionally convergent, meaning it converges with the specific arrangement of terms but not when terms are replaced by their magnitudes alone, which would diverge.
- 🔄 The difference between absolute and conditional convergence is highlighted, with absolute convergence allowing for rearrangement of terms without changing the sum.
- 💡 A conditionally convergent series' sum can change based on the order of terms, which is a unique property not found in finite arithmetic.
- ⚠️ The caution against 'monkeying with conditional convergence' is emphasized, as changing the order of terms can lead to incorrect results.
- 📘 Supplementary notes are recommended for further understanding, including proofs and exercises to solidify the concepts discussed in the lecture.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is 'Absolute Convergence,' which discusses series where terms are not all positive and the concept of convergence in such cases.
Why did the lecturer choose the specific series 1 - 1/2 + 1/3 - 1/4 + 1/5, etc., for the illustration?
-The lecturer chose this series because it is a straightforward example of an alternating series with terms that are not all positive, which helps to illustrate the concept of absolute convergence.
What are the three properties of an alternating series mentioned in the lecture?
-The three properties of an alternating series are: the terms alternate in sign, the n-th term approaches 0, and the terms decrease monotonically in magnitude.
How does the lecturer intend to show that the series 1 - 1/2 + 1/3 - 1/4 + 1/5, etc., converges?
-The lecturer intends to show the convergence of the series geometrically, by demonstrating that the sequence of partial sums approaches a limit.
What is the significance of the series 1 - 1/2 + 1/3 - 1/4 + 1/5, etc., having a limit of the natural log of 2?
-The significance is that it demonstrates a case where a series converges, but the limit is not immediately obvious and requires proof, highlighting the difference between Cauchy convergence and knowing the exact limit.
What is the definition of absolute convergence given in the lecture?
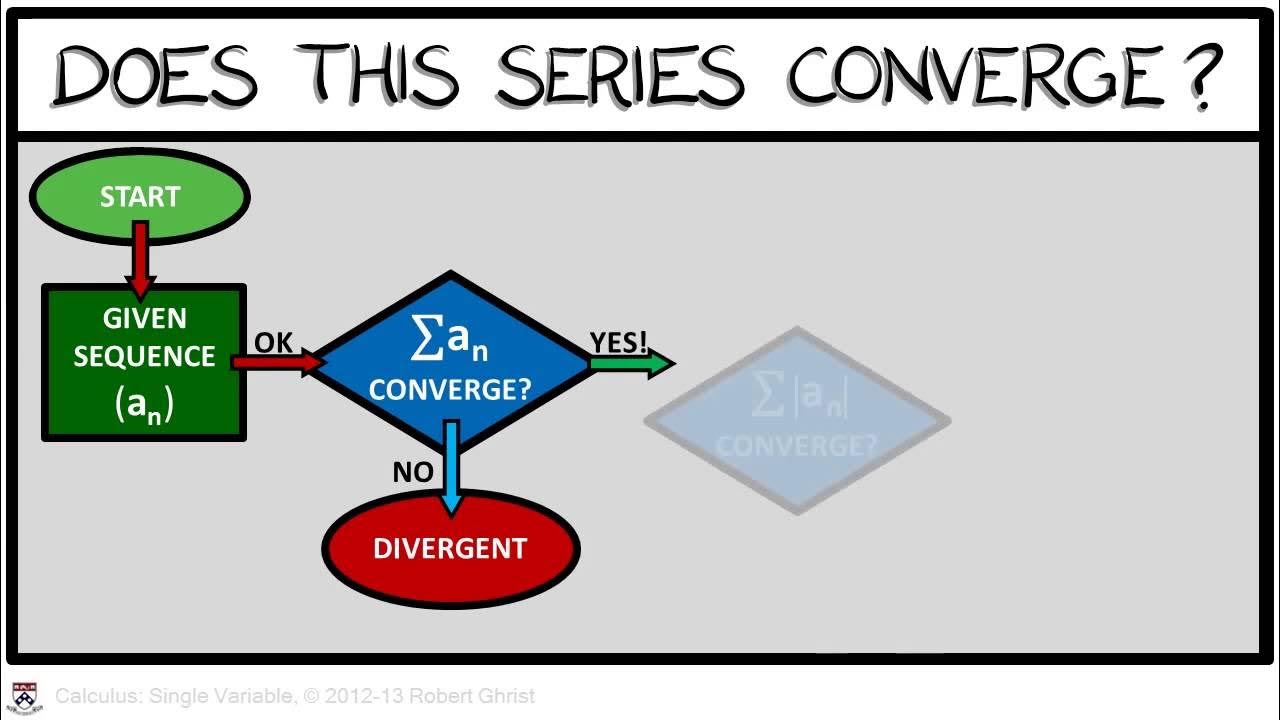
-A series is said to converge absolutely if the series obtained by replacing each term with its magnitude converges.
Why is it important to distinguish between absolute and conditional convergence?
-It is important because an absolutely convergent series can be rearranged in any order without changing the sum, while a conditionally convergent series may have a different sum if the order of terms is changed.
What is the difference between a conditionally convergent series and an absolutely convergent series in terms of rearranging terms?
-A conditionally convergent series can have a different sum when the order of terms is changed, whereas the sum of an absolutely convergent series remains the same regardless of the order of terms.
What does the lecturer mean by 'Don't monkey with conditional convergence'?
-The lecturer is cautioning against altering the order of terms in a conditionally convergent series, as doing so can lead to a different sum and potentially incorrect results.
Why does the lecturer emphasize the importance of absolute convergence for numerical manipulations of series?
-The lecturer emphasizes this because absolute convergence allows for the flexibility to rearrange terms in a series without affecting the sum, which is crucial for numerical calculations and manipulations.
What is the final advice given by the lecturer regarding conditionally convergent series?
-The final advice is to add the terms of a conditionally convergent series in the order they appear to ensure the correct limit, as changing the order can result in a different limit.
Outlines
📚 Introduction to Absolute Convergence
The first paragraph introduces the concept of absolute convergence in the context of series with non-positive terms. It highlights the importance of understanding series convergence when not all terms are positive, which was a condition in previous assignments. The lecturer, Herbert Gross, sets the stage for the lecture by discussing the series 1 - 1/2 + 1/3 - 1/4 + ..., explaining its properties and how it converges despite the alternating signs. The focus is on the series' behavior, such as terms approaching zero and decreasing in magnitude, which are key to its convergence.
🔍 Exploring Convergence and Absolute Values
In this paragraph, the discussion delves into the geometric proof of the convergence of the alternating series introduced earlier. The lecturer emphasizes that the convergence is due to the cancellation of positive and negative terms rather than the rate at which the terms approach zero. The concept of absolute convergence is introduced by considering the series obtained by replacing each term with its absolute value, which in this case, leads to a divergent series. The paragraph concludes with a definition of absolute convergence and the assertion that an absolutely convergent series also converges in the traditional sense.
📉 Conditional Convergence and Its Subtleties
The third paragraph explores the implications of conditional convergence, where a series converges but not absolutely. The lecturer uses the example of the series 1 - 1/2 + 1/3 - 1/4 + ... to illustrate that rearranging the terms can change the sum of a conditionally convergent series. This is a stark contrast to finite arithmetic, where the order of terms does not affect the sum. The paragraph introduces the idea that the sum of a conditionally convergent series is sensitive to the order of its terms, a subtlety not present in finite sums.
🔄 The Impact of Rearranging Terms in Conditional Convergence
This paragraph delves deeper into the consequences of rearranging terms in a conditionally convergent series. The lecturer demonstrates that by selectively adding positive and negative terms, one can manipulate the sum to any desired value. This is illustrated by attempting to achieve a sum of 3/2 through strategic addition of terms from the series. The paragraph emphasizes the importance of not altering the order of terms in conditionally convergent series to avoid obtaining incorrect sums.
📘 The Advantages of Absolute Convergence
The final paragraph contrasts the properties of absolutely convergent series with those of conditionally convergent ones. It highlights the freedom to rearrange terms in absolutely convergent series without affecting the sum, a luxury not available with conditionally convergent series. The lecturer stresses the importance of recognizing absolute convergence when dealing with series to avoid the pitfalls associated with conditional convergence. The paragraph ends with a reminder to review supplementary notes for a deeper understanding and to prepare for future discussions on the topic.
🙌 Conclusion and Call to Support
The concluding paragraph serves as a final reminder for viewers to consult the supplementary notes and engage with the exercises to solidify their understanding of the material. It also acknowledges the funding provided by the Gabriella and Paul Rosenbaum Foundation for the publication of the video and encourages viewers to support MIT OpenCourseWare to continue offering free educational resources. The paragraph ends with a farewell from the lecturer until the next session.
Mindmap
Keywords
💡Creative Commons license
💡Absolute Convergence
💡Conditionally Convergent
💡Alternating Series
💡Convergence
💡Divergence
💡Integral Test
💡Magnitude
💡Partial Sums
💡Natural Logarithm
Highlights
Introduction to the concept of 'Absolute Convergence' and its significance in series where terms are not all positive.
Exploration of series convergence when terms are not uniformly positive, challenging the stringent condition of positivity in previous assignments.
Illustration of a specific alternating series with terms that oscillate between -1 and 1, and a mathematical trick using powers of -1 to alternate signs.
Identification of three key properties of an alternating series: sign alternation, n-th term approaching 0, and monotonically decreasing magnitude.
Geometric proof of convergence for the alternating series 1 - 1/2 + 1/3 - 1/4 + ..., without analytical methods.
Demonstration of partial sums and their behavior in an alternating series, showing how the series 'closes in' on a limit.
Revelation that the limit of the series 1 - 1/2 + 1/3 - 1/4 + ... is the natural logarithm of 2, highlighting the difference between convergence and knowing the limit.
Definition and explanation of 'Absolute Convergence' in the context of series where terms are replaced by their magnitudes.
The importance of absolute convergence for series that can be rearranged without affecting the sum, unlike conditionally convergent series.
Differentiation between 'absolutely convergent' and 'conditionally convergent' series, and the implications for the series' behavior.
The subtlety of conditional convergence where the sum of a series can change based on the order of terms.
Practical example of how rearranging terms in a conditionally convergent series can yield any desired sum, contradicting the properties of finite arithmetic.
Warning against altering the order of terms in conditionally convergent series to avoid obtaining incorrect results.
Emphasis on the reliability of absolute convergence for numerical manipulations and the freedom it provides in rearranging terms.
The supplementary notes' role in providing detailed proofs and intuitive explanations for the concepts discussed in the lecture.
Final advice on the importance of understanding the difference between absolute and conditional convergence for proper handling of series in mathematics.
Transcripts
Browse More Related Video

Absolute and Conditional Convergence
Calculus Chapter 5 Lecture 53 Absolute & Conditional

AP Calculus BC Lesson 10.9

Alternating Series, Types of Convergence, and the Ratio Test

Calculus 2 Lecture 9.6: Absolute Convergence, Ratio Test and Root Test For Series

Sum of an infinite geometric series | Sequences, series and induction | Precalculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: