AP Calculus BC Lesson 10.9

Elizabeth Fein

22 Jan 202323:17

EducationalLearning

32 Likes 10 Comments

TLDRThis lesson delves into the concepts of absolute and conditional convergence, primarily in the context of alternating series. It explains that a series is absolutely convergent if both the series itself and the series of its absolute values converge. The lesson uses the alternating series test to demonstrate convergence and provides examples to illustrate absolute and conditional convergence. It also presents a flowchart for handling alternating series and discusses the tests for determining whether a series diverges, converges conditionally, or converges absolutely.

Takeaways

📘 Alternating series convergence is determined using the alternating series test, which requires the limit of the non-alternating portion to approach zero and that portion to be decreasing.
📊 An infinite series is absolutely convergent if both the series itself and the series of its absolute values converge.
🔄 Conditional convergence occurs when an infinite series converges, but the series of its absolute values diverges.
🌐 Example: The series 1/n^3 converges absolutely because it satisfies the p-series test with p > 1 when considering the absolute values.
📈 The harmonic series (1/n) diverges, which can be determined by the divergence of the p-series test with p = 1.
🔢 To determine absolute versus conditional convergence, compare the behavior of the series with a known convergent or divergent series using limit comparison.
📌 When faced with a series of the form -1^n * a_n, the alternating portion -1^n is what causes the series to alternate between positive and negative terms.
🧩 If a series is given with a non-standard variable (like K instead of n), the process for determining convergence remains the same, just with the variable switched.
📝 For a series to be absolutely convergent, both the original series and the series with absolute values applied must converge to a finite value.
🔍 When analyzing a series, first determine if it converges or diverges using the appropriate tests, then classify the convergence as absolute or conditional based on the behavior of the absolute values.

Q & A

What are the main topics discussed in this lesson?
-The main topics discussed in this lesson are absolute convergence and conditional convergence, primarily used with alternating series.
How is an infinite series considered absolutely convergent?
-An infinite series is considered absolutely convergent if both the series from n equals 1 to Infinity of a_n and the series from n equals 1 to Infinity of the absolute value of a_n converge.
What is the alternating series test, and how is it used?
-The alternating series test is a method used to determine the convergence of an alternating series. It requires the limit as n approaches Infinity of the non-alternating portion of the series to be equal to zero and for that portion to be decreasing.
What does the absolute value do in the context of series convergence?
-The absolute value makes all terms of the series positive, effectively removing the alternating sign and allowing the series to be analyzed as a non-alternating series.
How can you identify a conditionally convergent series?
-A series is conditionally convergent if the overall series converges, but the series of the absolute value of its terms diverges.
What is the difference between an absolutely convergent and a conditionally convergent series?
-An absolutely convergent series converges both with and without the alternating signs, whereas a conditionally convergent series only converges when the alternating signs are present.
What is the significance of the limit of the non-alternating portion in determining series convergence?
-The limit of the non-alternating portion must approach zero for the alternating series test to be applicable. This is one of the two conditions for a series to be considered convergent by this test.
What happens when the non-alternating portion of a series is decreasing?
-If the non-alternating portion of a series is decreasing, it contributes to the series being potentially convergent, as it is one of the conditions for convergence in the alternating series test.
How does the P-series test relate to the convergence of a series?
-The P-series test is used to determine the convergence of a series where the general term is of the form 1/n^p. If the value of p is greater than 1, the series converges; if p is less than or equal to 1, the series diverges.
What is the role of the limit comparison test in analyzing series convergence?
-The limit comparison test is used to compare the behavior of two series to determine if one converges or diverges based on the other. If one series converges and the other behaves similarly, then the compared series also converges.

Outlines

00:00

📚 Introduction to Absolute and Conditional Convergence

This paragraph introduces the concepts of absolute and conditional convergence, primarily in the context of alternating series. It explains that a series is absolutely convergent if both the original series and the series of its absolute values converge. The paragraph uses an example to illustrate the concept and mentions the alternating series test, which is further explained in a separate video. The example demonstrates how to determine if a series is absolutely convergent by checking the convergence of the non-alternating portion and its decreasing nature.

05:01

🔍 Analyzing Series Convergence: Conditional vs. Absolute

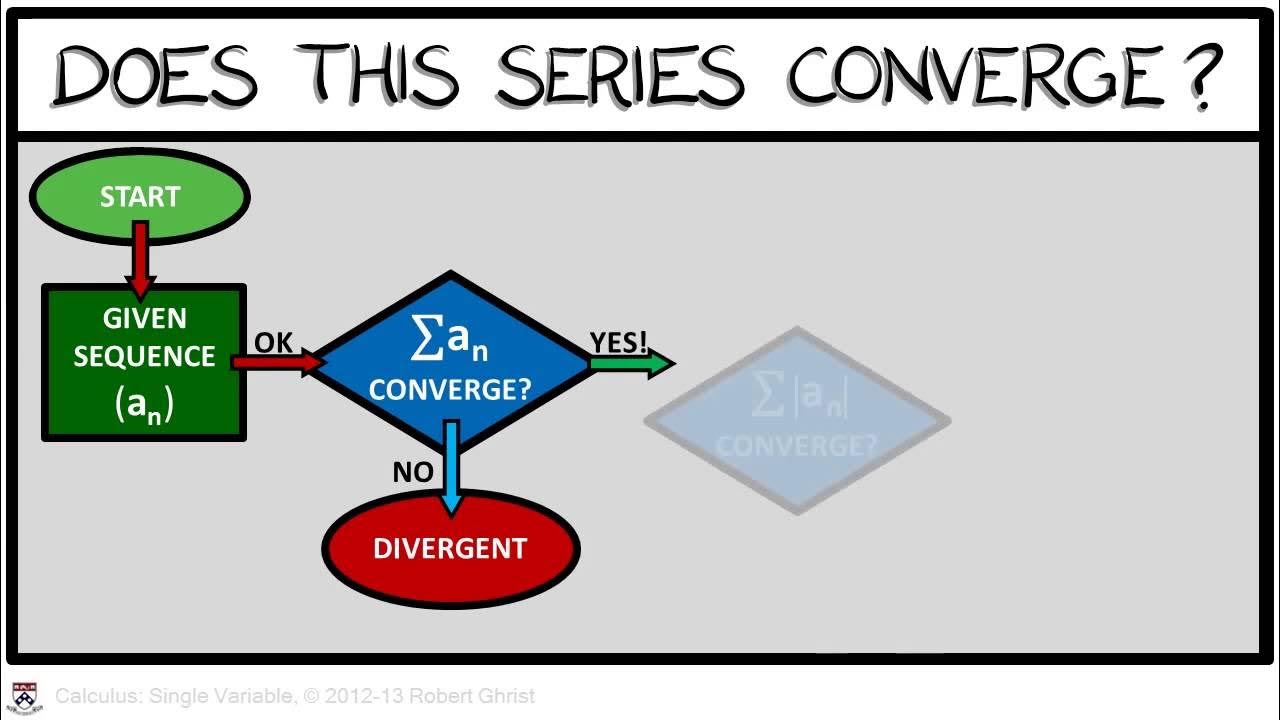
The paragraph delves into the process of determining whether a series is conditionally or absolutely convergent. It outlines the alternating series test for overall convergence and explains the need to check if the non-alternating portion of the series converges and is decreasing. The paragraph provides an example of a conditionally convergent series, where the series converges, but the series of absolute values diverges. It also introduces a flowchart for dealing with alternating series, emphasizing the importance of first determining if the series converges or diverges before exploring the type of convergence.

10:01

📈 Applying the Alternating Series Test to Specific Cases

This paragraph applies the alternating series test to various cases to determine convergence. It explains how to handle series with different forms, such as those involving terms to the power of n, and how to use the test to establish convergence or divergence. The paragraph also discusses the implications of the test results, such as when a series diverges, it cannot be conditionally convergent. It provides detailed calculations and reasoning for each case, including the use of limit comparisons and the P-series test to further analyze the series.

15:02

🤔 Evaluating Convergence in Complex Series

The paragraph examines the convergence of more complex series, including those with alternating signs and those that involve functions like cosine. It explains how to treat the alternating signs and apply the alternating series test to determine convergence. The paragraph also discusses how to assess absolute convergence by examining the behavior of the series without the alternating signs. It provides a detailed analysis of each series, including the use of limit comparisons and the P-series test, to determine whether the series is conditionally or absolutely convergent.

20:04

🎯 Conclusion: Identifying Absolutely Convergent Series

In the final paragraph, the focus is on identifying which series are absolutely convergent. It revisits the process of determining convergence using the alternating series test and absolute value considerations. The paragraph provides a detailed analysis of a specific series to demonstrate how to establish absolute convergence, using limit comparisons and other mathematical tests. It concludes by identifying the series that are conditionally and absolutely convergent, summarizing the key points and providing clarity on the concepts discussed throughout the video script.

Mindmap

Keywords

💡Absolute Convergence

Absolute convergence refers to a type of convergence in infinite series where both the original series and the series of its absolute values converge. In the context of the video, this is determined by checking if the series from n equals 1 to infinity of the absolute value of a sub n converges. An example from the script is the series that converges because both the original and the absolute value series (1 over n cubed) converge.

💡Conditional Convergence

Conditional convergence occurs in an infinite series when the overall series converges, but the series of the absolute values of its terms does not. This concept is important in the video as it helps differentiate between series that converge due to their alternating signs and those that would diverge if those signs were removed. An example provided in the script is a series that converges by the alternating series test but whose absolute value series (1 over n) diverges, indicating conditional convergence.

💡Alternating Series Test

The Alternating Series Test is a method used to determine the convergence of an alternating series, which is a series where the terms alternate in sign. The test checks two conditions: the limit of the non-alternating portion of the series as n approaches infinity must be zero, and the non-alternating portion must be decreasing. The video uses this test to analyze various series and determine their convergence properties.

💡Series Convergence

Series convergence refers to the process where the sum of an infinite series approaches a finite value as the number of terms increases without bound. In the video, the concept is central to understanding the behavior of different types of series, such as alternating series and absolute value series. The determination of convergence is crucial for applying various tests and understanding the properties of the series.

💡Limit

In mathematics, a limit is the value that a function or sequence approaches as the input (or index) approaches some value. In the context of the video, limits are used to evaluate the convergence of series, particularly in the Alternating Series Test where the limit of the non-alternating portion of the series as n approaches infinity is considered.

💡Decreasing Sequence

A decreasing sequence is one where each term is less than the term that follows. In the context of the video, the concept is used to describe the non-alternating portion of a series to ensure it meets one of the conditions for the Alternating Series Test. A sequence is considered decreasing if, as the index increases, the value of the sequence decreases.

💡Geometric Series

A geometric series is an infinite series where each term is a constant ratio multiplied by the previous term. The video discusses the geometric series in the context of determining absolute convergence, where the series is rewritten to identify if it is a geometric series and then tested for convergence based on the value of the common ratio.

💡Divergent Series

A divergent series is one that does not converge; that is, the sum of its terms does not approach a finite value as the number of terms increases. In the video, identifying a series as divergent is important as it helps to understand the behavior of the series and to apply the correct tests for convergence.

💡Non-Alternating Portion

The non-alternating portion of a series refers to the part of the series that remains when the alternating signs are removed. This concept is crucial in the video when determining the convergence of a series, especially in the context of the Alternating Series Test and when checking for absolute convergence.

💡P-Series Test

The P-Series Test, also known as the p-test, is a method for determining the convergence or divergence of an infinite series where the terms form a geometric progression with a common ratio. The test compares the absolute value of the ratio (p) to 1, with the series converging if the absolute value of p is less than 1 and diverging if it is greater than or equal to 1. The video uses this test to analyze the convergence of series without alternating signs.

💡Limit Comparison Test

The Limit Comparison Test is a method used to determine the convergence or divergence of two series by comparing their terms' limits as the number of terms approaches infinity. If the limit of the ratio of the corresponding terms of the two series exists and is a positive finite number, the series have the same behavior regarding convergence or divergence. The video uses this test to compare series and make conclusions about their convergence properties.

Highlights

The lesson focuses on absolute and conditional convergence, primarily in relation to alternating series.

A series is absolutely convergent if both the series and its absolute values converge.

An example is provided to demonstrate how to prove a series is absolutely convergent.

Conditional convergence occurs when a series converges overall, but the series of absolute values diverges.

A flowchart is introduced to help determine whether an alternating series is divergent, conditionally convergent, or absolutely convergent.

The alternating series test is used to determine if a series with an alternating portion converges or diverges.

For absolute convergence, the non-alternating portion of the series must also converge.

A series can be shown to diverge by not meeting the criteria of the alternating series test.

The convergence of a series can also be determined by comparing it to a known divergent or convergent series.

The lesson provides a comprehensive explanation of how to apply the alternating series test to various scenarios.

The importance of determining the convergence type (absolute or conditional) is emphasized for a deeper understanding of series behavior.

A series that converges absolutely will have its non-alternating portion decrease at a rate faster than the alternating portion.

The lesson concludes with a multiple-choice question to test understanding of the concepts taught.

The process of determining convergence involves both the alternating and non-alternating portions of a series.

The lesson explains how to handle series with different types of terms, such as those involving powers of n.

The application of limit comparison tests is discussed for determining the convergence of series.

The lesson provides a clear and detailed explanation of the concepts of absolute and conditional convergence, making complex mathematical ideas accessible.

Transcripts

Browse More Related Video

Absolute and Conditional Convergence

Conditional and Absolute Convergence for Infinite Series

Calculus BC – 10.9 Determining Absolute or Conditional Convergence

Calculus Chapter 5 Lecture 53 Absolute & Conditional

Alternating Series, Types of Convergence, and the Ratio Test

Conditional & absolute convergence | Series | AP Calculus BC | Khan Academy

Related Tags

Mathematics Alternating Series Convergence Tests Absolute Convergence Conditional Convergence Infinite Series Math Tutorial Educational Content Math Analysis Series Divergence