Calculus 2 Lecture 9.6: Absolute Convergence, Ratio Test and Root Test For Series

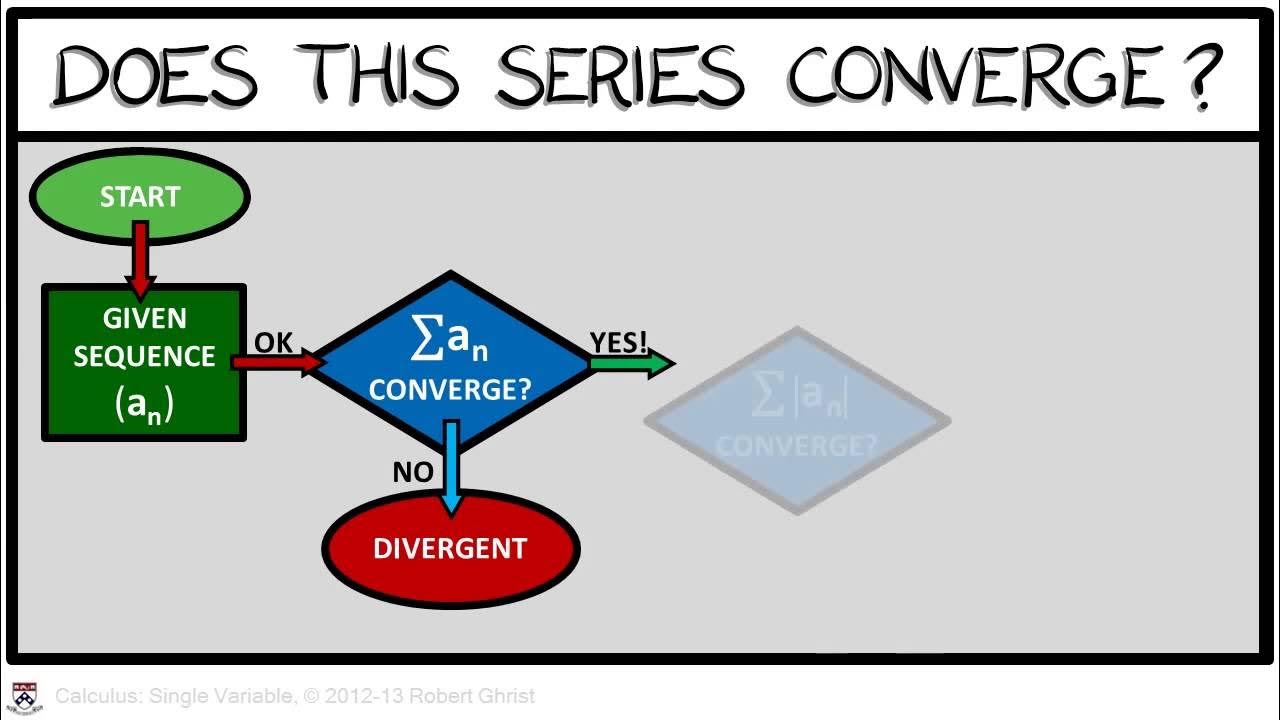
This paragraph introduces the concept of absolute convergence in series analysis. It discusses how to handle negative terms in series testing, emphasizing that while tests like the integral and comparison tests require positive terms, absolute convergence allows for negative terms by considering the absolute value of the series. The speaker promises to explain absolute convergence, its application, and two powerful tests based on this concept, one of which is the ratio test. An example of a series that does not alternate and is not always positive or decreasing is mentioned, setting the stage for the explanation of absolute convergence.

The speaker delves into absolute convergence by providing examples and explaining how it differs from simple convergence. They illustrate how taking the absolute value of a series can lead to a new series that, if convergent, implies the original series is absolutely convergent. The concept is clarified using the series of 1/n^2, which is shown to be absolutely convergent. The importance of absolute convergence is highlighted by demonstrating that a series can be convergent but not absolutely convergent, as seen with the alternating harmonic series, leading to the concept of conditional convergence.

This section clarifies the difference between absolutely convergent and conditionally convergent series. The speaker uses the alternating harmonic series as an example to explain that a series can be convergent without being absolutely convergent. They emphasize that absolute convergence is a stronger condition than simple convergence, and that any absolutely convergent series is guaranteed to be convergent. The concept is reinforced by discussing the implications of the absolute value on the convergence of a series.

The speaker discusses the application of absolute convergence in series analysis, specifically mentioning the series of sin(2n)/n^2 as an example. They explain that absolute convergence can be tested by examining the convergence of the series formed by taking the absolute value of the original series' terms. The comparison with the p-series is made, and the convergence of the series with the absolute value is used to infer the absolute convergence of the original series.

The paragraph introduces the ratio test, a powerful tool for series analysis. The test involves forming a ratio of consecutive terms of a sequence and taking the limit as n approaches infinity. The speaker outlines the outcomes of the ratio test: if the limit is less than one, the series is absolutely convergent; if greater than one, the series is divergent; and if equal to one, the test is inconclusive. An example is briefly mentioned to illustrate the application of the ratio test.

The speaker provides a detailed walkthrough of the ratio test using specific examples. They show how to calculate the limit of the ratio of consecutive terms and interpret the results to determine the convergence or divergence of a series. The examples illustrate how the ratio test can be used to establish absolute convergence or divergence, and the speaker emphasizes the test's utility in series analysis.

This section focuses on applying the ratio test to determine the convergence of various series. The speaker demonstrates how the test can be used to identify absolute convergence or divergence and how it simplifies the analysis of series with factorials and powers of n. The examples provided show the step-by-step process of using the ratio test and highlight its effectiveness as a 'goto' test for series analysis.

The speaker concludes the discussion by summarizing the various tests and techniques used in series analysis. They provide a recap of the divergence test, geometric series test, telescoping series test, p-series test, and the integral test. The speaker also outlines the conditions under which each test is applicable and emphasizes the importance of selecting the appropriate test based on the characteristics of the series in question.

This paragraph offers an overview of strategies for analyzing series convergence. The speaker suggests starting with the divergence test for all series and then considering the specific type of series, such as geometric, telescoping, or p-series. They also mention the integral test for functions that are positive, continuous, and decreasing. The speaker emphasizes the importance of understanding the characteristics of the series to choose the most efficient test.

The speaker discusses the comparison test and the limit comparison test for series analysis. They explain that these tests involve comparing the given series with a known series or taking the limit of the ratio of the terms of two series. The outcomes of these tests can help determine the convergence or divergence of the series in question, especially when the series terms are similar to those of a known series.

The paragraph focuses on the alternating series test, which is applicable when the series terms alternate in sign. The speaker outlines the two-part test: the limit of the first term must be zero, and the terms must be decreasing. If these conditions are met, the series is considered convergent.

The speaker provides guidance on choosing the appropriate test for series analysis based on the properties of the series. They discuss the ratio test for factorials and powers of n, and the root test for n powers. The speaker also emphasizes the importance of recognizing when to use the ratio test or the root test, and when to apply the comparison or limit comparison tests.

The speaker summarizes the series analysis techniques, providing a quick rundown of the tests and their applications. They highlight the divergence test, geometric and telescoping series tests, p-series test, integral test, comparison and limit comparison tests, alternating series test, ratio test, and root test. The speaker aims to ensure that the audience has a clear understanding of when and how to apply each test.