Absolute and Conditional Convergence

RH Mathematics
14 Feb 202405:46
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of absolute versus conditional convergence in alternating series. Starting with the alternating harmonic series, the presenter introduces the power series of the natural logarithm function and demonstrates how rearranging terms affects convergence, illustrating the idea of conditional convergence. The video defines absolute convergence as the convergence of a series when the absolute values of its terms are summed, contrasting it with conditional convergence, where the series converges but the sum of absolute values diverges. Examples of both types are provided, emphasizing that all infinite series in AP Calculus are either absolutely convergent, conditionally convergent, or divergent, with no series converging neither absolutely nor conditionally.

Takeaways
  • πŸ“š The video discusses alternating series and introduces the concepts of absolute and conditional convergence.
  • πŸ” The alternating harmonic series is used as an example to illustrate the concept of conditional convergence.
  • πŸ“˜ The natural log of 1 plus X is represented by a power series, which is introduced without expecting the audience to understand its derivation at this point.
  • πŸ”’ The series is simplified and rearranged to show how terms can be grouped to demonstrate the concept of conditional convergence.
  • πŸ”„ The commutative property of addition is highlighted, emphasizing that it applies to finite sums but not necessarily to infinite series.
  • πŸ“‰ The alternating harmonic series is shown to converge conditionally, meaning its convergence depends on the order of its terms.
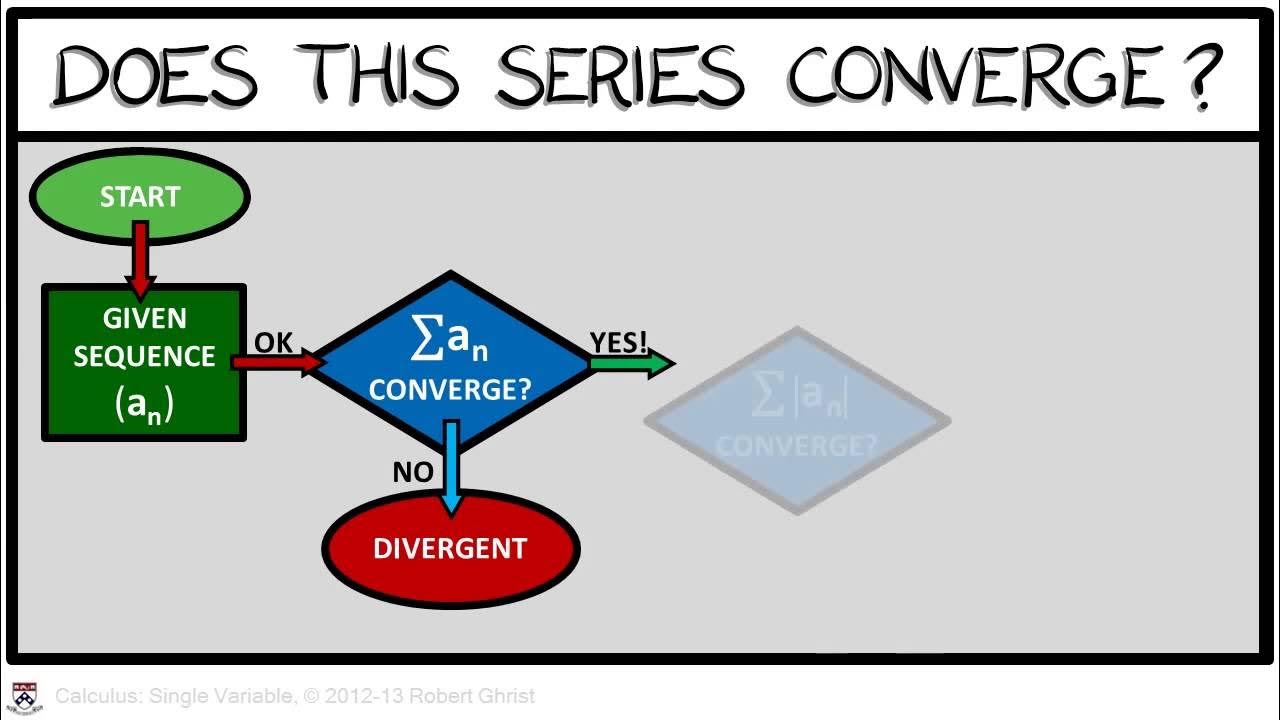
  • πŸ“ˆ Absolute convergence is defined as the convergence of a series when the sum of the absolute values of its terms also converges.
  • πŸ“Š Conditional convergence is defined as the convergence of a series where the sum of the absolute values of its terms diverges.
  • 🌐 An example of an absolutely convergent series is given, demonstrating how the sum of 1 over n squared converges.
  • πŸŒ€ An example of a conditionally convergent series is provided, showing how the sum of cosine of pi n over the square root of n converges but its absolute value series diverges.
  • πŸ“š The video concludes by stating that all infinite series are either absolutely convergent, conditionally convergent, or divergent, and warns against the non-existent option of converging neither absolutely nor conditionally.
Q & A

  • What is the main topic discussed in the video?

    -The main topic discussed in the video is the concept of absolute versus conditional convergence in the context of alternating series.

  • What is the alternating harmonic series mentioned in the script?

    -The alternating harmonic series is a series that starts with 1, -1/2, 1/3, -1/4, and so on, where the terms alternate in sign.

  • What is the power series representation of the natural log of (1 + x) mentioned in the script?

    -The script does not provide the explicit power series representation of the natural log of (1 + x), but it is implied to be a series similar to the alternating harmonic series and is accepted as a given fact for the purpose of the discussion.

  • Why does the script suggest accepting the power series for natural log of (1 + x) without proof?

    -The script suggests accepting the power series for natural log of (1 + x) without proof because it is not the focus of the video, and the audience is expected to trust this fact for the sake of the demonstration.

  • What does the script demonstrate by rearranging terms in the series?

    -The script demonstrates the idea of conditional convergence by rearranging terms in the series to show that the sum can change based on the order of terms, which is a characteristic of conditionally convergent series.

  • What is the difference between absolute and conditional convergence?

    -A series is absolutely convergent if the series of the absolute values of its terms also converges. A series is conditionally convergent if it converges, but the series of the absolute values of its terms diverges.

  • What is an example of an absolutely convergent series given in the script?

    -An example of an absolutely convergent series given in the script is the series with terms -1/(n^2 + 1), which converges because the series of the absolute values of its terms, 1/(n^2 + 1), also converges.

  • What is an example of a conditionally convergent series given in the script?

    -An example of a conditionally convergent series given in the script is the series with terms cos(Ο€n)/sqrt(n), which converges by the alternating series test, but the series of the absolute values of its terms, 1/sqrt(n), diverges.

  • What does the script state about the possible outcomes for infinite series in AP Calculus?

    -The script states that all infinite series in AP Calculus are either absolutely convergent, conditionally convergent, or divergent, and there is no series that converges but neither absolutely nor conditionally.

  • What is the significance of the commutative property in the context of the script?

    -The commutative property is mentioned in the script to highlight that it applies to finite addition, but not to the convergence of infinite series, which can be affected by the order of terms, as seen in conditional convergence.

  • What is the next topic the video series will cover according to the script?

    -According to the script, the next topic the video series will cover is the alternating series error bound.

Outlines
00:00
πŸ“š Alternating Series Convergence: Absolute vs. Conditional

This paragraph introduces the concept of alternating series convergence, distinguishing between absolute and conditional convergence. The video starts with the alternating harmonic series and uses the power series expansion of the natural logarithm function to demonstrate how rearranging terms affects convergence. The presenter rearranges the terms of the series to show that the sum can change, illustrating the concept of conditional convergence. The video also explains that the alternating harmonic series converges conditionally, unlike the regular harmonic series, which diverges. Definitions of absolute and conditional convergence are provided, with examples of each type of convergence. An absolutely convergent series is one where the series of absolute values of its terms also converges, while a conditionally convergent series converges but the series of absolute values of its terms diverges.

05:00
πŸ“˜ Understanding Series Convergence in AP Calculus

In this paragraph, the focus shifts to preparing for a multiple-choice test in AP Calculus, specifically addressing the three possible outcomes for series: absolute convergence, conditional convergence, or divergence. The presenter clarifies that there is no series that converges but neither absolutely nor conditionally, which is a common misconception. The paragraph emphasizes the importance of understanding these concepts for exam success. The video concludes by encouraging viewers to apply these definitions to determine the convergence type of alternating series, and promises to delve into the alternating series error bound in the next video, maintaining a focus on making the content accessible and digestible.

Mindmap
Keywords
πŸ’‘Alternating Series
An alternating series is a sequence of terms where the sign of each term alternates between positive and negative. This concept is central to the video's theme as it discusses the convergence of such series. In the script, the alternating harmonic series is used as an example, demonstrating how the series converges conditionally, not absolutely.
πŸ’‘Absolute Convergence
Absolute convergence refers to the property of a series where the sum of the absolute values of its terms converges. It is a stronger form of convergence than conditional convergence. The video explains that if a series converges absolutely, the order of its terms does not affect its sum, which is a key point in understanding the difference between absolute and conditional convergence.
πŸ’‘Conditional Convergence
Conditional convergence is a type of convergence where a series converges, but the series of the absolute values of its terms diverges. The video emphasizes this concept by showing that the alternating harmonic series converges conditionally, meaning that its sum is dependent on the order of its terms, unlike an absolutely convergent series.
πŸ’‘Natural Logarithm
The natural logarithm, denoted as ln(x), is the logarithm of a number to the base e, where e is the mathematical constant approximately equal to 2.71828. In the video, the natural logarithm of (1 + x) is expanded into a power series, which is a key step in demonstrating the concept of conditional convergence through the alternating series example.
πŸ’‘Power Series
A power series is an infinite series of the form \( \sum_{n=0}^{\infty} a_n (x - x_0)^n \), where \( a_n \) are the coefficients and \( x_0 \) is the center of the series. The script mentions the power series expansion of the natural logarithm function, which is crucial for the demonstration of the alternating series and its convergence properties.
πŸ’‘Alternating Harmonic Series
The alternating harmonic series is a specific type of series where the terms are the reciprocals of the natural numbers, with alternating signs. The video uses this series to illustrate the concept of conditional convergence, showing that despite the divergence of the regular harmonic series, the alternating version converges due to the alternating signs.
πŸ’‘Commutative Property
The commutative property states that the order in which two numbers are added does not change the sum, i.e., \( a + b = b + a \). The video script mentions this property in the context of rearranging terms in a series, highlighting that while it holds for finite addition, the convergence of an infinite series can be affected by the order of its terms.
πŸ’‘P-Series Test
The P-series test is a method used to determine the convergence of series of the form \( \sum_{n=1}^{\infty} \frac{1}{n^p} \), where p is a positive real number. The video uses this test to explain why certain series, like the one involving the cosine function, converge conditionally, while others, like the harmonic series, diverge.
πŸ’‘Cosine Function
The cosine function is a trigonometric function that describes a wave with a period of 2Ο€. In the script, the cosine function is used in the context of an example series to demonstrate how the terms of a series can alternate due to the periodic nature of the cosine function, leading to conditional convergence.
πŸ’‘Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In the video, the square root is used in the denominator of a series term to illustrate how the magnitude of terms decreases, which is a characteristic necessary for the series to potentially converge.
πŸ’‘Divergent Series
A divergent series is one where the sum of its terms does not approach a finite value as the number of terms increases. The video mentions that all infinite series are either absolutely convergent, conditionally convergent, or divergent, emphasizing that there is no series that converges but neither absolutely nor conditionally in the context of AP Calculus.
Highlights

Continuation of the discussion on alternating series.

Introduction of absolute versus conditional convergence in series.

Use of the alternating harmonic series as an example to start the discussion.

Presentation of the power series for natural log(1 + x) and its acceptance without proof.

Demonstration of plugging in x = 1 into the power series for natural log.

Simplification of the power series expression up to eight terms.

Rearrangement of terms to illustrate the concept of conditional convergence.

Explanation of how the commutative property applies to finite addition but not to series convergence.

Identification of the alternating harmonic series as an example of conditional convergence.

Definition of absolute convergence when the series of absolute term values also converges.

Definition of conditional convergence when the series of absolute term values diverges.

Example of an absolutely convergent series: alternating series with terms (-1)^(n+1)/n^2.

Use of the p-series test to confirm the absolute convergence of the example series.

Example of a conditionally convergent series involving cosine function and square root of n.

Explanation of why the series converges by the alternating series test but diverges when considering absolute values.

Clarification that all infinite series are either absolutely convergent, conditionally convergent, or divergent.

Advice against choosing the non-existent option of 'converges but neither absolutely nor conditionally' in AP Calculus.

Conclusion of the video with a summary of definitions and examples for understanding series convergence.

Preview of the next video topic: the alternating series error bound.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 10.9

Calculus Chapter 5 Lecture 53 Absolute & Conditional

Conditional and Absolute Convergence for Infinite Series

Unit VII: Lec 3 | MIT Calculus Revisited: Single Variable Calculus

Calculus 2 Lecture 9.6: Absolute Convergence, Ratio Test and Root Test For Series

Conditional & absolute convergence | Series | AP Calculus BC | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Alternating SeriesConvergence TypesConditional ConvergenceAbsolute ConvergenceCalculus TopicsMathematics EducationSeries TestNatural LogarithmPower SeriesInfinite Series