AP Calculus BC Exam Review - Geometric Series

turksvids

29 Apr 201811:02

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial provides an in-depth review of geometric series, a common topic in BC calculus exams. It covers the fundamental concept that geometric series converge only if the absolute value of the common ratio R is less than 1. The instructor demonstrates how to identify and sum geometric series, handle series with irrational numbers, and determine convergence using comparison tests. Additionally, the video explores transforming expressions into series, finding intervals of convergence, and emphasizes the importance of practice for exam preparation.

Takeaways

📚 Geometric series are a common topic on the BC Calculus exam and have a specific form involving a sum from a certain number to infinity of 'a' times 'R' to the power of 'N'.
🔍 The series converges only if the absolute value of 'R' is less than 1, which is a crucial concept to watch out for when determining if a series has a sum.
📝 The sum of a geometric series can be found using the formula: the first term divided by (1 - R), where 'R' is the common ratio.
🌐 Examples provided in the script illustrate how to identify and calculate the sum of geometric series, including handling cases with irrational and transcendental numbers.
⚠️ Beware of series where the absolute value of 'R' is greater than 1, as these do not converge and are often used to trick test-takers.
🤔 When faced with a series, it's important to first recognize if it's geometric and then determine if it converges by checking the absolute value of the ratio.
📉 The script also covers how to deal with series that are given in expanded form, by identifying the common ratio and first term to find the sum.
📈 Geometric series can be used to find new series from old ones, by leveraging the sum of a geometric series formula and manipulating terms.
📊 The script explains how to use the geometric series formula to rewrite complex expressions as infinite series, which can be useful in various mathematical contexts.
📐 The interval of convergence for a geometric series is determined by the condition that the absolute value of 'R' must be less than 1, excluding the endpoints.
📝 Practice is emphasized as essential for mastering geometric series, including using them for comparison tests and determining convergence of other series.

Q & A

What is a geometric series?
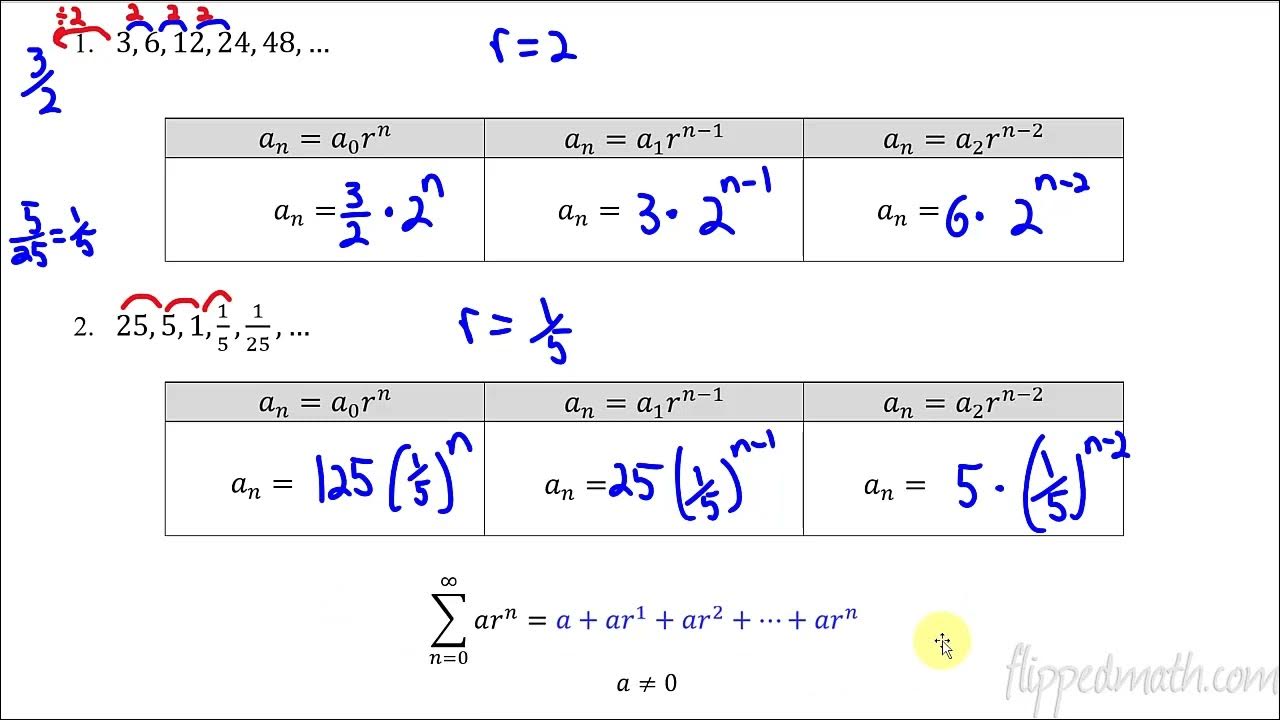
-A geometric series is an infinite series where each term after the first is found by multiplying the previous term by a constant called the common ratio (R).
What is the condition for a geometric series to converge?
-A geometric series converges if the absolute value of the common ratio (|R|) is less than 1.
How do you find the sum of a convergent geometric series?
-The sum of a convergent geometric series is found by dividing the first term by one minus the common ratio (S = a / (1 - R)), where 'a' is the first term.
What is the first term in the series 3 * (-4/5)^n starting from n=0?
-The first term in this series is 3, which is the term when n=0.
How do you determine if the series e/π^n from n=2 to infinity converges?
-Since e is less than π, the common ratio e/π is less than 1, ensuring the series converges.
What does it mean if the common ratio of a geometric series is greater than 1?
-If the common ratio is greater than 1, the series diverges, meaning it does not have a finite sum.
How can you identify a geometric series when terms are written out?
-You can identify a geometric series by dividing consecutive terms and checking if the result is a constant ratio, which is the common ratio (R).
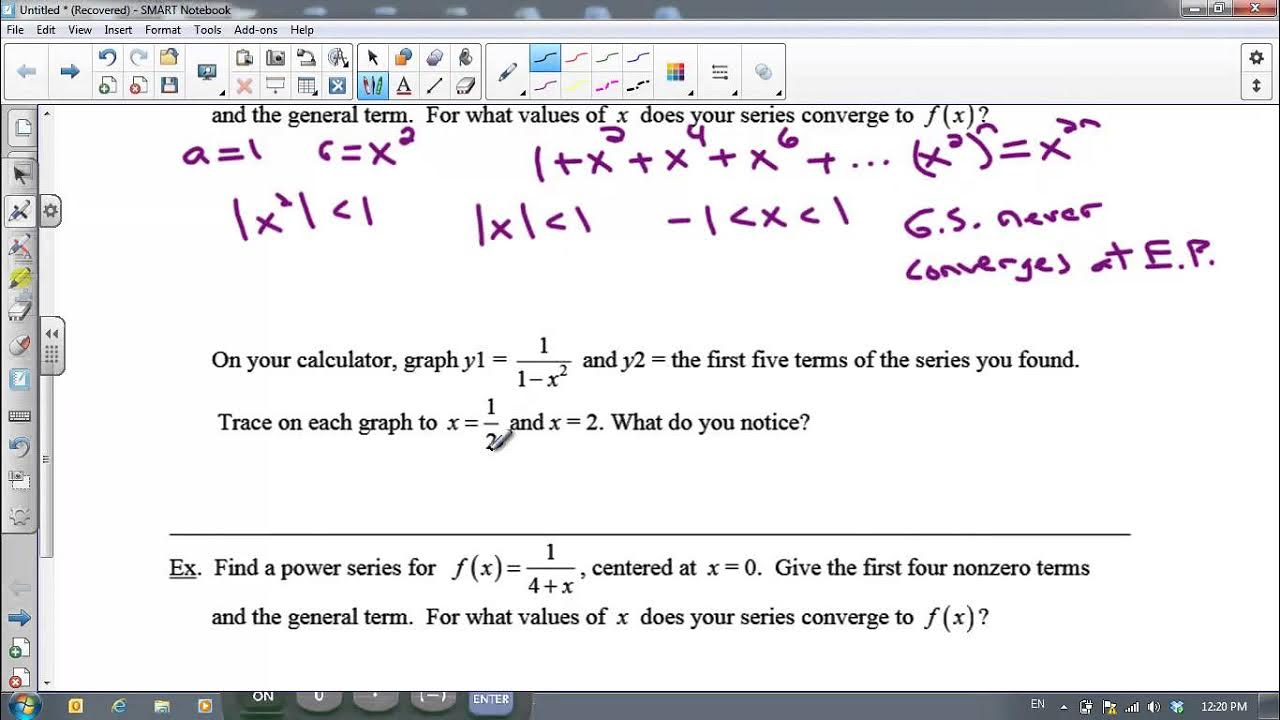
What is the sum of the series x^3 + 3x^5 + 9x^7 + 27x^9 + ...?
-The sum of this series is the first term (x^3) divided by 1 minus the common ratio (3x^2), provided |3x^2| < 1.
What is the interval of convergence for the series x^2 in the context of the script?
-The interval of convergence for the series involving x^2 is between -1/root(3) and 1/root(3), where x^2 < 1/3.
How can geometric series be used to determine the convergence of another series?
-Geometric series can be used to determine the convergence of another series by direct comparison. If a given series is less than a convergent geometric series term by term, then it also converges.
Can a geometric series ever converge at its endpoints?
-No, geometric series never converge at the endpoints of their interval of convergence.
How can you rewrite a rational function as a geometric series?
-You can rewrite a rational function as a geometric series by identifying the first term and common ratio, and then expressing the function as the sum of a series of terms involving the common ratio raised to increasing powers.

Outlines

00:00

📚 Introduction to Geometric Series

This paragraph introduces the concept of geometric series and their appearance on the BC Calculus exam. The speaker emphasizes the importance of recognizing the general form of a geometric series, which typically involves a sum from a certain number to infinity of a term raised to a power. The key takeaway is that the series converges only if the absolute value of the common ratio (R) is less than 1. Examples are provided to illustrate how to determine the first term and the sum of the series, highlighting the need to be cautious of series with absolute values of R greater than 1.

05:01

🔍 Analyzing and Summarizing Geometric Series

In this paragraph, the speaker delves deeper into the analysis of geometric series. They discuss how to determine if a series converges by checking the absolute value of the common ratio (R). Examples include series with irrational numbers and transcendental numbers, emphasizing the need to ensure R is in the correct range. The speaker also explains how to find the sum of a geometric series by identifying the first term and using the formula involving the first term and the reciprocal of (1 - R). Additionally, they explore how to handle series given in expanded form, checking for consistency in the common ratio and calculating the sum accordingly.

10:03

📉 Convergence and Comparison of Series

The final paragraph focuses on the convergence of series and how to compare them. The speaker discusses the use of geometric series in multiple-choice questions, where one might need to determine which series converge or diverge. They also touch on the direct comparison test, using geometric series to compare and determine the convergence of other series. The speaker provides an example of rewriting a given series as a geometric series to simplify the analysis. The paragraph concludes with a summary of the common types of questions involving geometric series that one might encounter on the exam, such as finding the actual sum or determining the interval of convergence.

Mindmap

Keywords

💡Geometric Series

A geometric series is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. In the video, the geometric series is the central topic, with the script discussing how to identify, sum, and determine the convergence of such series, particularly in the context of calculus exams.

💡Convergence

Convergence in the context of series refers to the property where the sum of an infinite series approaches a finite value. The script emphasizes that a geometric series converges if the absolute value of the common ratio is less than 1, which is a key concept for determining the sum of the series.

💡Common Ratio (R)

The common ratio, denoted as 'R' in the script, is the factor by which consecutive terms of a geometric series are multiplied. It is crucial in determining the behavior of the series, especially whether it converges or diverges. The script provides examples of how to identify and use the common ratio in calculations.

💡First Term

The first term of a series is the initial value from which subsequent terms are generated according to a specific rule. In the context of geometric series, the first term is used in the formula to find the sum of the series, as illustrated in the script with various examples.

💡Summation

Summation is the process of adding together all the terms of a series to find the total. The script explains how to calculate the sum of a geometric series by using the formula involving the first term and the common ratio, provided the series converges.

💡Absolute Value

The absolute value of a number is its distance from zero on a number line, regardless of direction, and is denoted by two vertical lines. In the script, the absolute value is used to determine if the common ratio of a geometric series is less than 1, a condition necessary for the series to converge.

💡Diverge

Divergent series are those whose sums do not approach a finite value but instead increase without bound. The script warns about identifying when a geometric series diverges, particularly when the common ratio's absolute value is not less than 1.

💡Ratio Test

The ratio test is a method used to determine the convergence of an infinite series by examining the limit of the absolute value of the ratio of consecutive terms. The script mentions using the ratio test to confirm the convergence of a series by ensuring the common ratio's absolute value is less than 1.

💡Direct Comparison Test

The direct comparison test is a technique used to establish the convergence of a series by comparing it to another series whose convergence is already known. The script uses this test to demonstrate the convergence of a series by comparing it to a geometric series with a known convergent behavior.

💡Interval of Convergence

The interval of convergence refers to the set of values for which a series converges. The script discusses how to determine this interval for a geometric series, especially when dealing with variable terms, and the importance of not including the endpoints if the series is geometric.

💡Transcendental Numbers

Transcendental numbers are numbers that are not the root of any non-zero polynomial equation with rational coefficients. In the script, transcendental numbers like 'e' and 'π' (pi) are mentioned in the context of determining the convergence of a series involving these numbers.

Highlights

Geometric series are a common type of series on the BC calculus exam.

Geometric series have a general form of the sum from some number to infinity of a times R to the N.

A series converges if the absolute value of R is less than 1.

The sum of a convergent geometric series is the first term over 1 minus the ratio.

Example given: Sum from zero to infinity of 3 times (-4/5) to the N.

The sum of the series can be simplified to 5/3.

Another example involves irrational numbers, such as e over PI to the N.

The ratio R must be within the range for a series to converge.

Geometric series can be used to determine if other series converge or diverge.

A series with a ratio greater than 1 diverges, as shown with radical seven over sine of one.

Geometric series can be identified by dividing consecutive terms to find the common ratio.

Example of finding the sum of a geometric series with terms written out.

The sum of a series can be expressed as a function, as shown with x cubed plus 3x to the fifth.

Geometric series can be used in the direct comparison test to determine convergence of other series.

Series can be rewritten as geometric series for analysis, such as 2x squared over 1 plus x squared.

The interval of convergence for a geometric series is determined by the absolute value of the ratio.

Geometric series will not converge at the endpoints of the interval of convergence.

Geometric series are frequently used in multiple-choice questions on the BC calculus exam.

The importance of practice in solving various types of problems involving geometric series.

Transcripts

Browse More Related Video

Ratio test | Series | AP Calculus BC | Khan Academy

Another derivation of the sum of an infinite geometric series | Precalculus | Khan Academy

Taylor Series Day 3

Power series of ln(1+x_) | Series | AP Calculus BC | Khan Academy

Calculus BC – 10.2 Working with Geometric Series

Sum of an infinite geometric series | Sequences, series and induction | Precalculus | Khan Academy

AP Calculus BC Exam Review - Geometric Series

Takeaways

Q & A

What is a geometric series?

What is the condition for a geometric series to converge?

How do you find the sum of a convergent geometric series?

What is the first term in the series 3 * (-4/5)^n starting from n=0?

How do you determine if the series e/π^n from n=2 to infinity converges?

What does it mean if the common ratio of a geometric series is greater than 1?

How can you identify a geometric series when terms are written out?

What is the sum of the series x^3 + 3x^5 + 9x^7 + 27x^9 + ...?

What is the interval of convergence for the series x^2 in the context of the script?

How can geometric series be used to determine the convergence of another series?

Can a geometric series ever converge at its endpoints?

How can you rewrite a rational function as a geometric series?