Ratio test | Series | AP Calculus BC | Khan Academy

Khan Academy
4 Sept 201408:58
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses geometric series, explaining the concept of a common ratio and its impact on series convergence. It demonstrates how an infinite series with a common ratio of absolute value less than one converges, and explores the ratio test to determine convergence of non-geometric series, concluding that a series converges if the limit of the ratio of consecutive terms approaches zero.

Takeaways
  • 🔍 The script discusses the concept of an infinite geometric series, highlighting the importance of the common ratio and its absolute value in determining convergence or divergence.
  • 📚 It is established that a geometric series converges if the absolute value of the common ratio is less than one, and diverges if it is greater than or equal to one.
  • 🔑 The common ratio is defined as the ratio between consecutive terms of the series, and in the case of a geometric series, it is constant.
  • 🤔 The script encourages revisiting videos on geometric series if the concepts are not familiar, emphasizing the importance of understanding the basics.
  • 🌟 The series is examined for convergence without being a geometric series, by looking at the behavior of the ratio between consecutive terms as N approaches infinity.
  • 🧐 The script introduces the idea of taking the limit of the ratio between consecutive terms to analyze the series' convergence, even when the series is not geometric.
  • 📉 The limit of the ratio between consecutive terms for the series in question approaches zero as N approaches infinity, suggesting convergence.
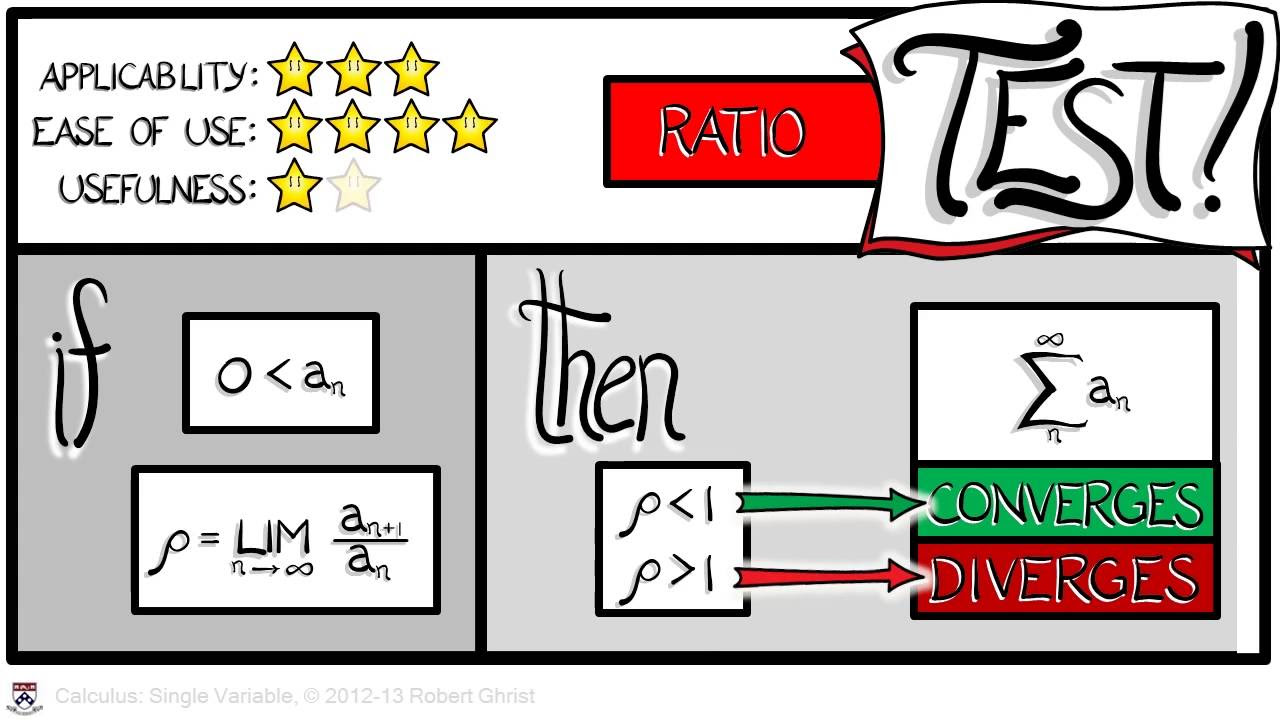
  • 📝 The ratio test is introduced as a method to determine the convergence of an infinite series by examining the limit of the absolute value of the ratio between consecutive terms.
  • 📊 The ratio test concludes that if the limit L is less than one, the series converges; if L is greater than one, it diverges; and if L equals one, the test is inconclusive.
  • 📚 The script uses the example of a series with terms involving N to the tenth power over N factorial to illustrate the application of the ratio test.
  • 🔗 The conclusion drawn is that the series in question converges, based on the limit of the ratio between consecutive terms approaching zero, aligning with the ratio test's criteria for convergence.
Q & A

  • What is a geometric series?

    -A geometric series is an infinite series where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio.

  • What is the common ratio in a geometric series?

    -The common ratio is the factor by which we multiply each term in the series to get the next term. In the given script, the common ratio is represented by 'R'.

  • What condition must the common ratio meet for a geometric series to converge?

    -For a geometric series to converge, the absolute value of the common ratio must be less than one.

  • What happens to a geometric series if the absolute value of the common ratio is greater than or equal to one?

    -If the absolute value of the common ratio is greater than or equal to one, the series diverges, meaning it does not approach a finite sum.

  • What is the purpose of the ratio test in series convergence?

    -The ratio test is used to determine the convergence of an infinite series. It involves examining the limit of the absolute value of the ratio of consecutive terms as they approach infinity.

  • How is the ratio test applied to a series that is not geometric?

    -The ratio test can be applied to any series by finding the limit of the absolute value of the ratio of consecutive terms. If this limit is less than one, the series converges.

  • What is the significance of the limit of the common ratio approaching zero in the script?

    -The limit of the common ratio approaching zero indicates that the terms of the series are getting smaller and smaller, suggesting that the series may converge.

  • What does it mean for a series to be absolutely convergent?

    -A series is absolutely convergent if the sum of the absolute values of its terms converges to a finite number. This implies that the series itself also converges.

  • How does the script demonstrate the application of the ratio test to a non-geometric series?

    -The script applies the ratio test to a series with terms of the form N to the tenth power over N factorial. By finding the limit of the ratio of consecutive terms as N approaches infinity, it shows that the series converges.

  • What is the conclusion of the script regarding the series with terms N to the tenth power over N factorial?

    -The script concludes that the series converges based on the ratio test, as the limit of the ratio of consecutive terms approaches zero as N goes to infinity.

Outlines
00:00
📚 Understanding Geometric Series and Convergence

This paragraph introduces the concept of an infinite geometric series, emphasizing the importance of the common ratio 'R'. It explains that if the absolute value of 'R' is less than one, the series converges, whereas if it's greater than or equal to one, the series diverges. The paragraph also reviews the idea that each term in the series is obtained by multiplying the previous term by 'R'. It then poses a question about the convergence of a series where the numerator grows faster than a polynomial, suggesting the use of intuition and the common ratio to explore this.

05:00
🔍 Applying the Ratio Test to Non-Geometric Series

The second paragraph delves into the application of the ratio test to series that are not geometric, using the example of a series with terms N to the tenth power over N factorial. It discusses the process of finding the ratio between consecutive terms and taking the limit as N approaches infinity. The paragraph demonstrates algebraic manipulation to simplify the ratio and concludes that the limit of this ratio is zero, indicating that the series converges. The ratio test is then explained as a method to determine the convergence of an infinite series by examining the limit of the absolute value of the ratio between consecutive terms. If this limit is less than one, the series is said to converge absolutely.

Mindmap
Keywords
💡Geometric Series
A geometric series is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. In the video, the concept is introduced with the series starting at N equals K to infinity of R to the N, illustrating how each term is derived by multiplying by the common ratio R. The series is a fundamental concept in the discussion of convergence and divergence of series.
💡Common Ratio
The common ratio in a geometric series is the factor by which each term is multiplied to get the next term. The script explains that the common ratio is crucial in determining the convergence or divergence of a series. If the absolute value of the common ratio is less than one, the series converges, as each term becomes smaller. This is a key concept in the video, used to explain the behavior of different series.
💡Convergence
Convergence in the context of series refers to the property of an infinite series where the sum of its terms approaches a finite limit. The video discusses how if the absolute value of the common ratio of a geometric series is less than one, the series converges to a finite value, illustrating the concept with the series starting at N equals K.
💡Divergence
Divergence in series is the opposite of convergence. It occurs when the sum of an infinite series does not approach a finite limit. The video script explains that if the absolute value of the common ratio is greater than or equal to one, the series diverges, meaning it does not have a finite sum.
💡Factorial
Factorial, denoted by an exclamation mark (!), is the product of all positive integers less than or equal to a given number. In the script, factorial is used in the series N to the tenth power over N factorial, highlighting how factorial growth is very rapid and plays a role in determining the convergence of the series.
💡Numerator
The numerator is the top number in a fraction. In the video, the numerator is N to the tenth power in the series N to the tenth power over N factorial, which is used to explore the behavior of the series as N increases.
💡Denominator
The denominator is the bottom number in a fraction. The script uses the denominator N factorial in the series to discuss how the ratio of consecutive terms changes and ultimately approaches zero, indicating convergence.
💡Limit
In mathematics, a limit is the value that a function or sequence approaches as the input approaches some value. The video discusses taking the limit as N approaches infinity of the ratio between consecutive terms to determine the convergence of the series, which is a key step in applying the ratio test.
💡Ratio Test
The ratio test is a method used to determine the convergence or divergence of an infinite series. The video explains that by taking the limit of the absolute value of the ratio of consecutive terms as N approaches infinity, one can conclude whether the series converges or diverges. If the limit is less than one, the series converges, which is demonstrated in the video with the series involving factorials.
💡Polynomial
A polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, and multiplication, and non-negative integer exponents of variables. The script mentions polynomials in the context of comparing the growth rate of factorials to high degree polynomials, emphasizing the rapid growth of factorials.
💡Absolute Value
The absolute value of a number is the non-negative value of the number without regard to its sign. In the video, the absolute value is discussed in the context of the common ratio and the ratio test, where it is used to determine the convergence or divergence of a series by considering the magnitude of the ratio, regardless of its sign.
Highlights

Introduction to geometric series and the concept of common ratio.

Explanation of the common ratio as the ratio between consecutive terms in a geometric series.

Clarification that the common ratio simplifies to R, the base ratio of the series.

Review of the convergence criteria for geometric series based on the absolute value of the common ratio.

Logical reasoning behind why a series with an absolute common ratio less than one converges.

Introduction of a non-geometric series example with N to the tenth power over N factorial.

Discussion on proving convergence of a series where the numerator grows faster than the denominator.

Attempt to find a common ratio for the non-geometric series by comparing consecutive terms.

Algebraic manipulation to simplify the ratio of consecutive terms in the series.

Observation that the ratio between consecutive terms is a function of N and not a fixed value.

Concept of examining the behavior of the series as N approaches infinity to determine convergence.

Limit calculation to find the behavior of the ratio between consecutive terms as N approaches infinity.

Conclusion that the ratio approaches zero, suggesting convergence of the series as N becomes very large.

Introduction of the ratio test as a method to determine the convergence of an infinite series.

Explanation of the ratio test criteria for determining convergence, divergence, or inconclusive results.

Application of the ratio test to the non-geometric series example to confirm its convergence.

Emphasis on the importance of the ratio test in analyzing series beyond simple geometric series.

Transcripts

Browse More Related Video

Another derivation of the sum of an infinite geometric series | Precalculus | Khan Academy

The Ratio Test

Worked example: interval of convergence | Series | AP Calculus BC | Khan Academy

Calculus Chapter 5 Lecture 52 Convergence Tests 2

Ratio Test

Sum of an infinite geometric series | Sequences, series and induction | Precalculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Geometric SeriesConvergence TestRatio TestAlgebraic LimitsFactorial GrowthPolynomial TermsInfinite SumsMathematics EducationSeries AnalysisEducational ContentMath Concepts