How to solve trigonometric equations using the Quadrant Rule

ExamSolutions

25 Aug 201421:17

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into solving trigonometric equations using the quadrant rule, focusing on the sine, cosine, and tangent functions. It explains the positivity and negativity of these functions across different quadrants and demonstrates solving equations with both positive and negative values of these trigonometric functions. The script guides viewers through the process of finding angles using inverse trigonometric functions, emphasizing the importance of understanding the quadrant rule for effective problem-solving in trigonometry.

Takeaways

📚 Trigonometric equations often involve finding the angle (theta) where sine, cosine, or tangent equals a specific value, either positive or negative.
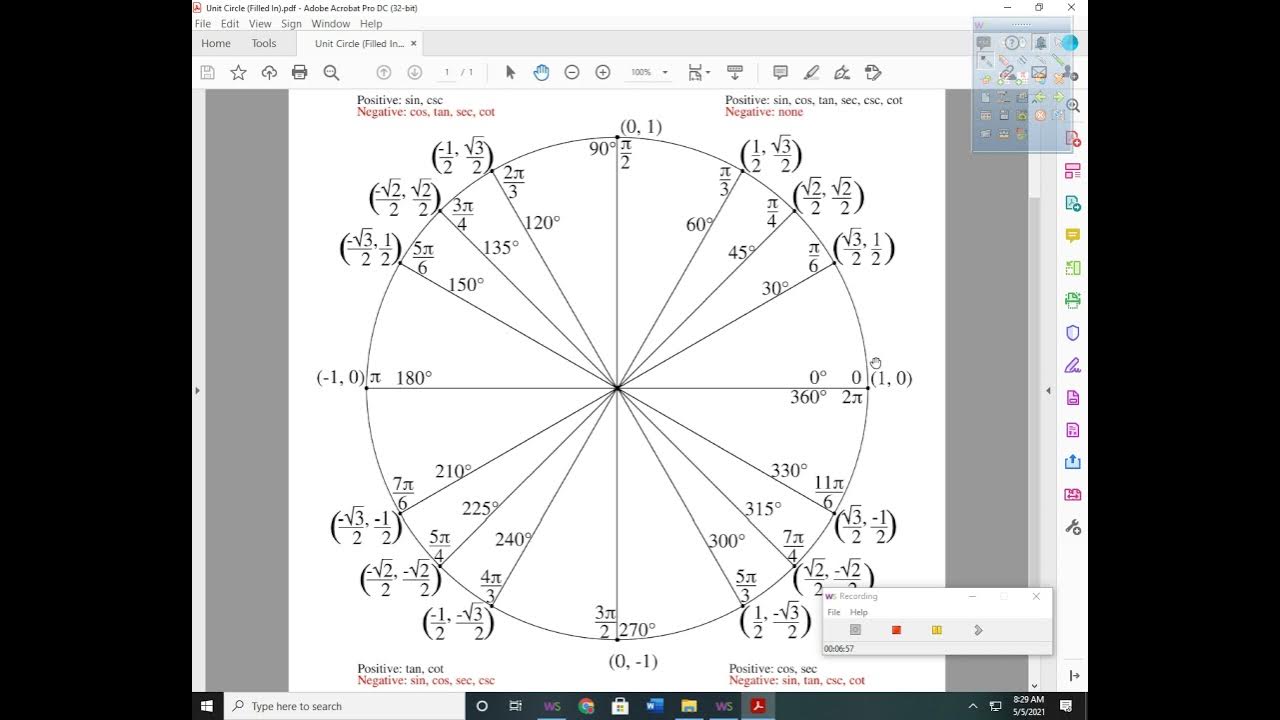
🌐 The quadrant rule is a method used to determine where trigonometric functions are positive or negative within the range of 0 to 360 degrees.
📈 In the first and second quadrants, all trigonometric functions (sine, cosine, tangent) are positive, while only sine is positive in the second quadrant.
📉 In the third and fourth quadrants, tangent is positive in the third quadrant and cosine is positive in the fourth quadrant.
🔍 The quadrant rule helps in solving trigonometric equations without the need to draw graphs, which can be time-consuming.
🔢 To find the angle theta, you can use inverse trigonometric functions like arcsine, arccosine, and arctangent.
🔄 Turning anti-clockwise from 0 degrees to 360 degrees is considered positive, while turning clockwise is negative.
🔄 Negative angles can be interpreted by turning clockwise on the quadrant diagram, and their magnitudes can still be used to find solutions.
📌 For equations like sine theta equals 0.5, solutions can be found in the first and second quadrants, with one solution being 30 degrees and the other 150 degrees.
📌 For equations with negative values, like sine theta equals -0.5, solutions are found in the third and fourth quadrants, with one solution being 210 degrees and the other 330 degrees.

Q & A

What is the main topic of the video?
-The main topic of the video is solving trigonometric equations using the quadrant rule for angles between 0 and 360 degrees.
What are the three trigonometric functions discussed in the video?
-The three trigonometric functions discussed are sine, cosine, and tangent.
What is the quadrant rule mentioned in the video?
-The quadrant rule is a method to determine the signs of sine, cosine, and tangent in the four quadrants of the unit circle, which helps in solving trigonometric equations.
How many solutions does the video suggest for the equation sine theta equals 0.5?
-The video suggests two solutions for the equation sine theta equals 0.5: 30 degrees and 150 degrees.
What is the range of angles considered in the video?
-The range of angles considered in the video is from 0 to 360 degrees.
How does the video handle negative values in trigonometric equations?
-The video handles negative values by using the quadrant rule to determine the correct quadrants where the function is negative and then finding the corresponding angles.
What is the process to find the second solution for an equation using the quadrant rule?
-The process involves finding the first solution, then using the symmetry of the trigonometric functions to find the second solution, often by subtracting the first solution from 180 degrees or adding to 180 degrees, depending on the quadrant.
Why does the video mention turning anti-clockwise and clockwise?
-Turning anti-clockwise and clockwise is mentioned to explain the direction of angle measurement on the unit circle, which is important for understanding the quadrant rule and solving equations.
What does the video suggest for solving equations with cosine theta equals 0.5?
-The video suggests using the quadrant rule to find that cosine is positive in the first and fourth quadrants, leading to solutions of 60 degrees and 300 degrees.
How does the video approach equations with tangent theta equals root 3?
-The video uses the quadrant rule to identify where tangent is positive (first and third quadrants), and then finds the angle using the inverse tangent function, resulting in a solution of 60 degrees.

Outlines

00:00

📚 Introduction to Solving Trigonometric Equations

This paragraph introduces the concept of solving trigonometric equations involving sine, cosine, or tangent of an angle theta, which can result in positive or negative values. The speaker explains the use of the quadrant rule for angles between 0 and 360 degrees, inclusive. The rule helps determine the sign of the trigonometric functions in different quadrants. The speaker also recaps previous content about the graphs of y = sine(x), y = cos(x), and y = tan(x) and their signs in different quadrants, emphasizing the quadrant rule's utility in solving equations without drawing graphs.

05:02

🔍 Solving Equations with Positive Sine Theta

The speaker demonstrates solving equations where sine theta equals a positive value, such as sine theta = 0.5. Using the quadrant rule, the speaker identifies that sine is positive in the first and second quadrants. Two possible solutions for theta are calculated using the inverse sine function, resulting in 30 degrees and 150 degrees. The explanation includes how to find these solutions on the unit circle and emphasizes the symmetry of the sine function graph.

10:04

📉 Solving Equations with Negative Sine Theta

In this section, the speaker addresses equations with a negative sine value, like sine theta = -0.5. The quadrant rule is used to determine that sine is negative in the third and fourth quadrants. Two possible solutions for theta are identified, and the inverse sine function is applied to find the angles, resulting in -30 degrees and 330 degrees. The speaker explains how to interpret negative angles on the unit circle and how to find the corresponding positive angles within the 0 to 360-degree range.

15:05

📐 Solving Equations with Cosine and Tangent

The speaker extends the method to solve equations involving cosine and tangent functions, both positive and negative. For cosine theta = 0.5, the positive solutions are found in the first and fourth quadrants, resulting in 60 degrees and 300 degrees. For cosine theta = -0.5, the negative solutions are in the second and third quadrants, yielding 120 degrees and 240 degrees. Similarly, for tangent theta = √3 and tangent theta = -√3, the speaker shows how to find the solutions using the inverse tangent function, emphasizing the importance of considering the correct quadrants for each function.

20:07

🔚 Conclusion and Future Exploration

In the concluding paragraph, the speaker summarizes the process of solving trigonometric equations with positive and negative values for sine, cosine, and tangent. They mention the importance of understanding the diagrams and quadrants for solving these equations effectively. The speaker also hints at future videos that will explore different ranges and more complex scenarios, such as equations involving multiples of theta.

Mindmap

Keywords

💡Trigonometric equations

Trigonometric equations involve the use of sine, cosine, and tangent functions to solve for angles. In the context of the video, these equations are solved by understanding the signs of these functions in different quadrants of the unit circle. The script discusses how to find the values of theta when the sine, cosine, or tangent is given as a positive or negative value.

💡Quadrant rule

The quadrant rule is a method used to determine the sign of trigonometric functions in the four quadrants of the Cartesian coordinate system. It is central to the video's theme as it provides a systematic way to solve trigonometric equations by identifying where sine, cosine, and tangent are positive or negative. The script explains that sine is positive in the first and second quadrants, cosine is positive in the first and fourth quadrants, and tangent is positive in the first and third quadrants.

💡Inverse sine (sin⁻¹)

The inverse sine function, denoted as sin⁻¹, is used to find the angle whose sine is a given value. In the video, it is used to solve for theta when the sine of theta is provided. For example, when sine theta equals 0.5, the script demonstrates that theta can be found by calculating the inverse sine of 0.5, resulting in an angle of 30 degrees.

💡Inverse cosine (cos⁻¹)

Similar to inverse sine, the inverse cosine function, or cos⁻¹, is used to determine the angle for a given cosine value. The video script illustrates this by showing how to find theta when cosine theta is 0.5, using the inverse cosine function to get an angle of 60 degrees.

💡Inverse tangent (tan⁻¹)

The inverse tangent function, tan⁻¹, is utilized to find an angle when the tangent of that angle is known. The script uses this function to solve for theta in cases where the tangent of theta is a specific value, such as root 3 or minus root 3, to find angles in the first and third quadrants where tangent is positive, and in the second and fourth quadrants where it is negative.

💡First quadrant

The first quadrant is the region of the Cartesian plane where both x and y coordinates are positive. In the video, it is mentioned that all trigonometric functions are positive in the first quadrant, which is crucial for solving equations where sine, cosine, and tangent are positive.

💡Second quadrant

The second quadrant is where x coordinates are negative, and y coordinates are positive. The script explains that sine is the only trigonometric function that is positive in the second quadrant, which is important when solving equations with sine theta being positive.

💡Third and fourth quadrants

The third quadrant is where both x and y coordinates are negative, and the fourth quadrant is where x coordinates are positive, and y coordinates are negative. The video script uses these quadrants to illustrate where tangent is positive in the third quadrant and cosine is positive in the fourth quadrant, aiding in solving trigonometric equations with negative values.

💡Positive and negative values

The script discusses solving trigonometric equations with both positive and negative values for sine, cosine, and tangent. Understanding the sign of these functions is essential for determining the correct quadrant and thus the correct angle solutions for theta.

💡Graphs of trigonometric functions

The video script refers to the graphs of y = sine x, y = cos x, and y = tan x to visually demonstrate the behavior of these functions across different quadrants. These graphs are crucial for understanding the quadrant rule and for identifying the ranges where the functions are positive or negative.

Highlights

Introduction to solving trigonometric equations using the quadrant rule for angles between 0 and 360 degrees.

Recap of the graph of y = sine(x), y = cos(x), and y = tan(x) to demonstrate the positive and negative values in different quadrants.

Explanation of the quadrant rule for determining the sign of trigonometric functions in different quadrants.

Demonstration of solving the equation sine theta equals 0.5 using the quadrant rule and inverse sine.

Finding two solutions for theta when sine theta is positive: 30 degrees and 150 degrees.

Illustration of the symmetry in trigonometric graphs to find the second solution for theta.

Solving the equation sine theta equals -0.5, identifying where sine is negative in the third and fourth quadrants.

Calculating the negative angle solution for theta as -30 degrees and its interpretation on the quadrant diagram.

Determining the positive angle solutions for theta as 210 degrees and 330 degrees from the negative angle.

Approach to solving equations with cosine theta equals 0.5, focusing on where cosine is positive.

Finding solutions for theta using the inverse cosine function: 60 degrees and 300 degrees.

Solving the equation with cosine theta equals -0.5, identifying the negative cosine values in the second and third quadrants.

Calculating the solutions for theta as 120 degrees and 240 degrees using inverse cosine.

Solving the equation tan theta equals the positive value of root 3, focusing on where tangent is positive.

Determining the solutions for theta as 60 degrees and 240 degrees using inverse tangent.

Solving the equation tan theta equals -root 3, identifying where tangent is negative in the second and fourth quadrants.

Calculating the solutions for theta as 120 degrees and 300 degrees from the negative tangent value.

Emphasis on the importance of understanding the quadrant rule for solving various trigonometric equations.

Outlook on future videos covering different ranges and more complex trigonometric scenarios.

Transcripts

Browse More Related Video

How to solve trigonometric equations with negative angles

Trigonometry: How to use the ASTC Rule | The Quadrant | CAST

Using Sum and Difference Formulas in Trigonometry (Precalculus - Trigonometry 26)

5.5 Multiple Angle and Product to Sum Formulas (Part 1)

How To Find The Exact Value of the Five Remaining Trigonometric Functions

Calculus AB Homework Day 2 - Review 2: Functions and Trig

Related Tags

Trigonometry Quadrant Rule Sine Function Cosine Function Tangent Function Graph Analysis Inverse Trigonometry Math Education Problem Solving Educational Video