How to solve trigonometric equations with negative angles

ExamSolutions
26 Aug 201415:34
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video explores solving trigonometric equations within different angle ranges. It demonstrates finding solutions for equations involving tangent, secant, and sine functions, using quadrant diagrams and inverse trigonometric functions. The video guides through determining the correct angle values within specified ranges, such as -360 to 0 degrees and -180 to 180 degrees, and highlights the importance of considering the range when solving for angles.

Takeaways
  • 📚 The video discusses extending the work on quadrant solutions by examining different ranges for solutions.
  • 🔍 The script covers solving equations involving trigonometric functions for specific angle ranges, starting with tan(theta) = √3 for angles between -360° and 0°.
  • 📏 It explains that tan(theta) = √3 has positive values and identifies the first and third quadrants as where tan is positive.
  • 📉 The video demonstrates how to use a quadrant diagram to find the solutions for the given range, highlighting the importance of considering both positive and negative angles.
  • 🔢 For tan(theta) = √3, the solutions are found by taking the inverse tan of √3, yielding an angle of 60°, and then adjusting for the given range to find -120° and -300°.
  • 📐 The second example involves sec(theta) = -2, with the range being -180° to 180°, focusing on where cosine is negative, i.e., the second and third quadrants.
  • 🔎 By rearranging sec(theta) = -2 to cos(theta) = -1/2, the video identifies the solutions as 120° and -120°, using the inverse cosine function.
  • 🌐 The third example deals with 2sin(theta) = √3, with a broad range of -720° to 720°, and identifies where sine is positive, i.e., the first and second quadrants.
  • 📈 The solutions for 2sin(theta) = √3 are derived by taking the inverse sine of √3/2, resulting in an angle of 30°, and then considering additional solutions by adding multiples of 360°.
  • 🔠 The video emphasizes the importance of considering the full range of possible solutions, including both positive and negative angles, and the use of inverse trigonometric functions to find specific angles.
Q & A

  • What is the purpose of the video?

    -The purpose of the video is to extend the work on quadrant solutions by looking at different ranges for solving trigonometric equations involving angles.

  • What are the different angle ranges discussed in the video?

    -The video discusses ranges from -360 to 0 degrees, -180 to 180 degrees, and -720 to 720 degrees.

  • Why is there no plus or minus value when solving for tan(theta) = √3?

    -The video specifies that only the positive value is taken for tan(theta) = √3, as the context implies a positive tangent value.

  • In which quadrants is the tangent of an angle positive?

    -The tangent of an angle is positive in the first and third quadrants.

  • How many solutions are there for the equation 10θ = √3 in the given range?

    -There are two solutions for the equation 10θ = √3 within the specified range: -120 degrees and -300 degrees.

  • What is the range for the second question involving sec(theta)?

    -The range for the second question with sec(theta) is from -180 to 180 degrees inclusive.

  • What does the equation 1/sec(theta) = -2 imply about the cosine of theta?

    -The equation 1/sec(theta) = -2 implies that cosine of theta is -1/2 after rearranging and solving for cos(theta).

  • In which quadrants is the cosine of an angle negative?

    -The cosine of an angle is negative in the second and third quadrants.

  • What are the two solutions for the equation sec(theta) = -2 within the specified range?

    -The two solutions for the equation sec(theta) = -2 are 120 degrees and -120 degrees.

  • What is the range for the third question involving 2sin(theta)?

    -The range for the third question with 2sin(theta) is from -720 to 720 degrees inclusive.

  • What does the equation 2sin(theta) = √3 simplify to?

    -The equation 2sin(theta) = √3 simplifies to sin(theta) = √3/2 after dividing both sides by 2.

  • In which quadrants is the sine of an angle positive?

    -The sine of an angle is positive in the first and second quadrants.

  • How many solutions are there for the equation 2sin(theta) = √3 in the given range?

    -There are multiple solutions for the equation 2sin(theta) = √3 within the specified range, including 30 degrees, 390 degrees, 150 degrees, 510 degrees, -210 degrees, -570 degrees, -330 degrees, and -690 degrees.

Outlines
00:00
📐 Introduction to Solving Trigonometric Equations with Quadrant Diagrams

In this video, we will extend our work on solving trigonometric equations using quadrant diagrams. We'll explore solutions within various ranges, starting with solving tan(θ) = √3 for θ in the range -360° to 0°. We emphasize the importance of understanding where tan(θ) is positive and use quadrant diagrams to visualize and solve the equation. The solutions are found by considering negative angles and calculating specific values: -120° and -300°.

05:02
➕ Solving sec(θ) = -2 in a Common Range

Next, we solve sec(θ) = -2 for θ in the range -180° to 180°. We convert sec(θ) to its reciprocal form, 1/cos(θ), and find where cos(θ) = -1/2. Using quadrant diagrams, we identify the relevant quadrants where cosine is negative. The solutions are found by considering both positive and negative angles, resulting in θ = ±120°.

10:02
🔄 Solving 2sin(θ) = √3 in an Extended Range

We solve 2sin(θ) = √3 for θ in the extended range -720° to 720°. By simplifying to sin(θ) = √3/2, we identify the quadrants where sine is positive. We find multiple solutions within this large range by considering additional rotations (360° increments) in both positive and negative directions. The solutions include: 30°, 150°, 390°, 510°, -210°, -330°, -570°, and -690°.

15:03
📊 Summary and Techniques for Trigonometric Solutions

The video concludes with a summary of the techniques used to solve trigonometric equations within specified ranges using quadrant diagrams. The importance of understanding positive and negative angle rotations is emphasized, along with how to systematically find all possible solutions within a given range.

Mindmap
Keywords
💡Quadrant
A quadrant refers to one of the four equal parts of a plane that is divided by the two axes of a Cartesian coordinate system. In the context of the video, the quadrant is used to determine the signs of trigonometric functions, such as tangent, sine, and cosine, which is crucial for solving trigonometric equations within specific ranges of angles.
💡Tangent
Tangent is a trigonometric function that is defined as the ratio of the length of the opposite side to the length of the adjacent side in a right-angled triangle. In the video, tangent is used to find the angle whose tangent value is the square root of 3, which is a key step in solving the given trigonometric equation.
💡Inverse Tangent
Inverse Tangent, often abbreviated as arctan or tan^-1, is the inverse function of the tangent and is used to find an angle given the tangent of that angle. In the video, the inverse tangent is used to find the angle whose tangent is the square root of 3, which is essential for determining the solutions within the specified angle ranges.
💡Degrees
Degrees are a unit of measurement for angles, with a full circle being 360 degrees. In the video, different ranges of degrees are considered for solving trigonometric equations, such as from -360 to 0 degrees and from -180 to 180 degrees, which are crucial for determining the correct range of solutions.
💡Secant
Secant is the reciprocal of the cosine function, denoted as sec(theta) = 1/cos(theta). In the video, the secant function is used in the context of solving an equation where the secant of an angle is given as -2, which helps in finding the angle within the specified range.
💡Inverse Cosine
Inverse Cosine, often abbreviated as arccos or cos^-1, is the inverse function of the cosine and is used to find an angle given the cosine of that angle. In the video, the inverse cosine is used to solve for the angle when the cosine of the angle is -1/2, which is a step in finding the solutions to the trigonometric equation.
💡Sine
Sine is a trigonometric function that relates the ratio of the lengths of the sides of a right-angled triangle. In the video, the sine function is used to solve an equation where 2 times the sine of an angle equals the square root of 3, which is a key part of determining the angle's value within a wide range of degrees.
💡Inverse Sine
Inverse Sine, often abbreviated as arcsin or sin^-1, is the inverse function of the sine and is used to find an angle given the sine of that angle. In the video, the inverse sine is used to find the angle when the sine of the angle is the square root of 3 divided by 2, which helps in identifying the angle's value within the given range.
💡Range
In mathematics, a range refers to the set of possible values for an independent variable, often used in the context of functions. In the video, the term 'range' is used to describe the intervals of angles within which the solutions to trigonometric equations must be found, such as from -360 to 720 degrees.
💡Solution
A solution in the context of equations refers to the value(s) of the variable that make the equation true. In the video, the term 'solution' is used to describe the specific angles that satisfy the given trigonometric equations within their respective ranges, such as 60 degrees, -120 degrees, and others.
💡Trigonometric Equations
Trigonometric Equations are equations that involve trigonometric functions and are used to find the angles that satisfy the given conditions. In the video, the main theme revolves around solving various trigonometric equations by identifying the correct angles within specified ranges, which is a fundamental concept in trigonometry.
Highlights

Introduction to solving trigonometric equations over different ranges.

Explanation of solving tan(theta) = sqrt(3) for theta in the range -360 to 0 degrees.

Identification of positive tan values in the first and third quadrants.

Steps to draw the quadrant diagram and find the relevant angles.

Calculating theta by taking the inverse tan of sqrt(3) to get 60 degrees.

Explanation of why 60 degrees is not in the specified range and how to adjust for the correct solutions.

Deriving the solutions of theta as -120 degrees and -300 degrees for the given range.

Explanation of solving sec(theta) = -2 for theta in the range -180 to 180 degrees.

Converting sec(theta) to 1/cos(theta) and solving for cos(theta).

Finding where cosine is negative and identifying the second and third quadrants.

Calculating theta by taking the inverse cos of -1/2 to get 120 degrees.

Deriving the solutions of theta as 120 degrees and -120 degrees for the given range.

Explanation of solving 2sin(theta) = sqrt(3) for theta in the range -720 to 720 degrees.

Dividing by 2 to solve for sin(theta) and identifying positive sine values in the first and second quadrants.

Steps to draw the quadrant diagram and find multiple solutions within the given range.

Calculating theta by taking the inverse sine of sqrt(3)/2 to get 30 degrees.

Deriving multiple solutions by adding and subtracting 360 degrees as needed.

Listing all valid solutions for theta in the range -720 to 720 degrees, including positive and negative angles.

Summary of how to solve and draw diagrams for trigonometric equations with specified ranges.

Transcripts

Browse More Related Video

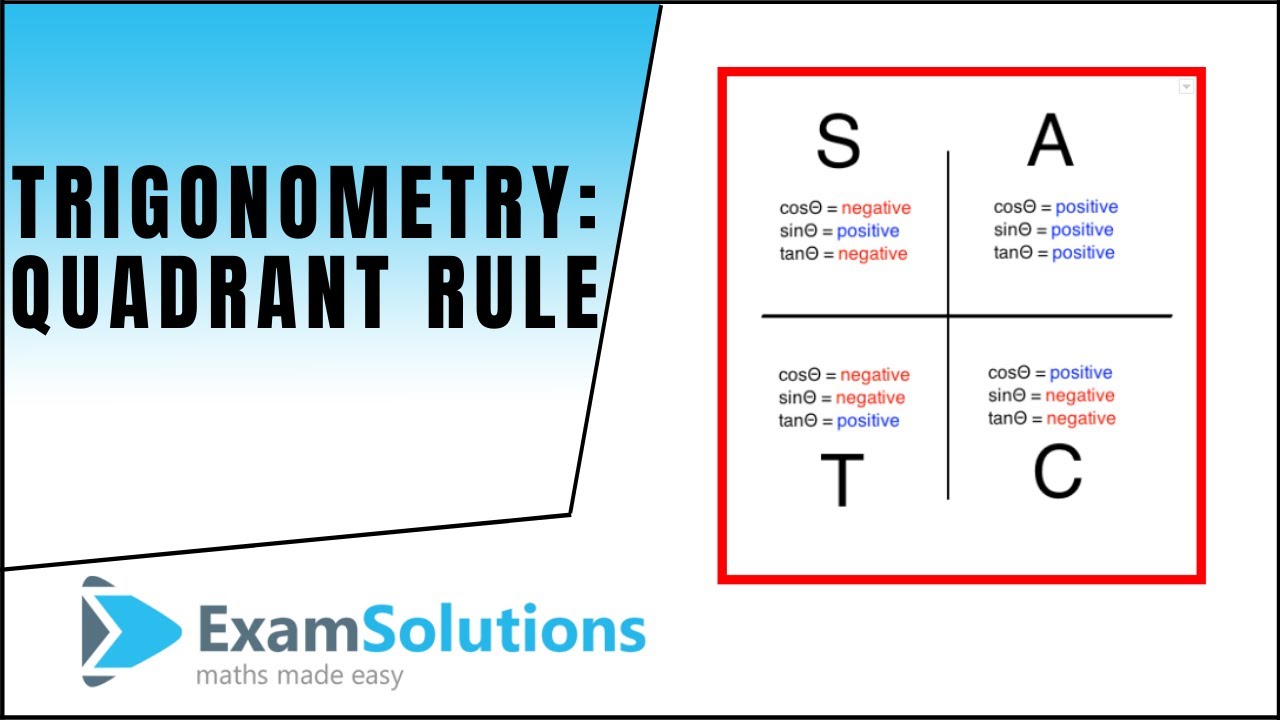
Trigonometry - Quadrant rule : Solving Sin θ = negative value : ExamSolutions

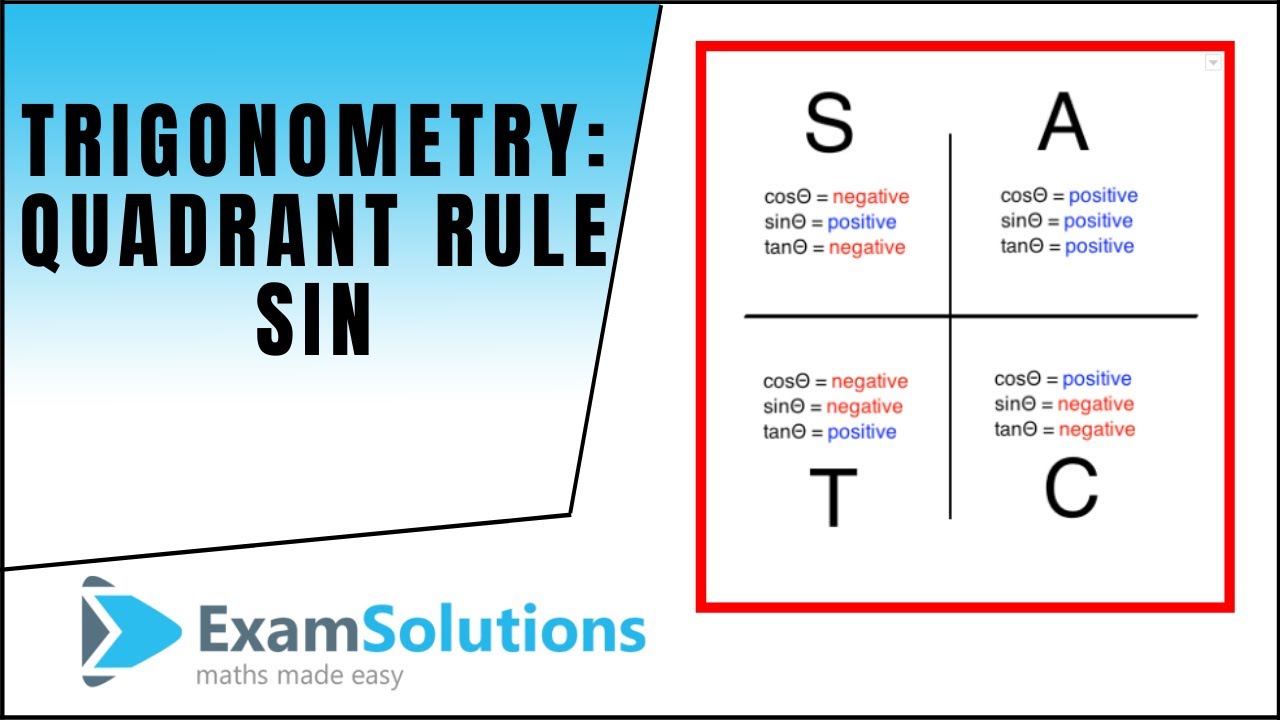
Trigonometry - Quadrant rule : Solving Sin θ = a positive value : ExamSolutions

How to solve trigonometric equations using the Quadrant Rule

REFERENCE ANGLES || PRE-CALCULUS

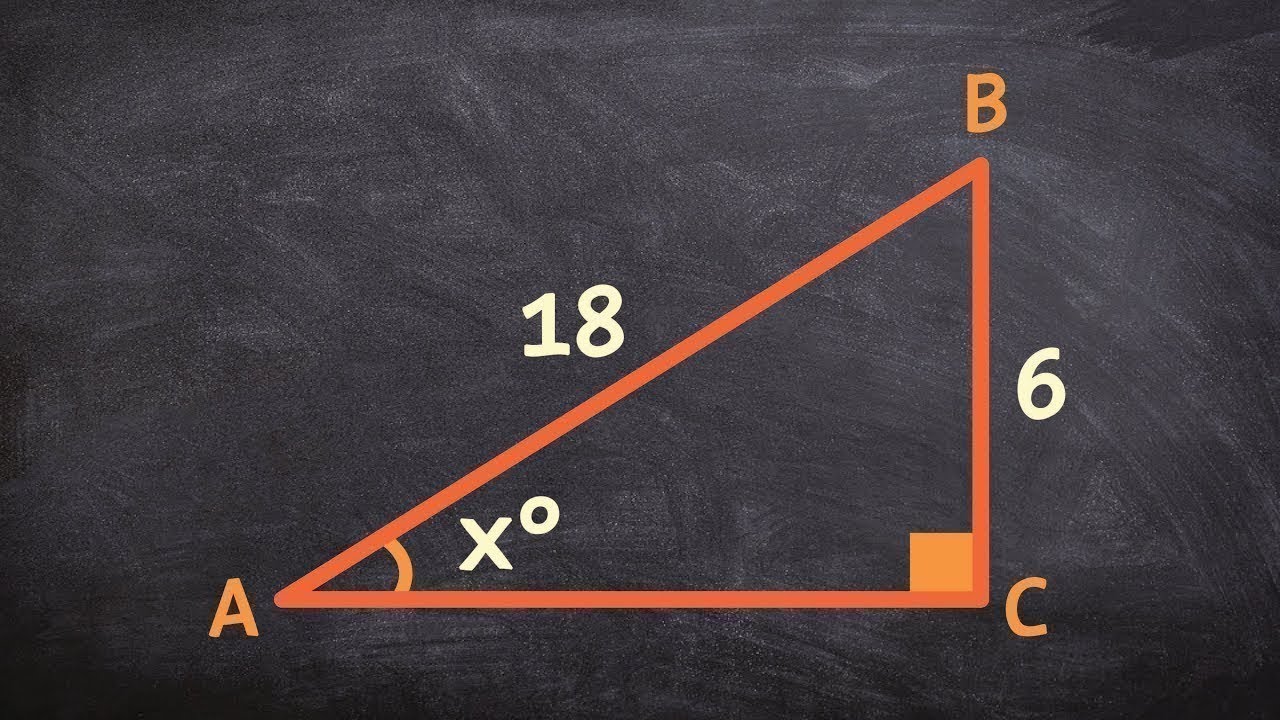
Learn to find the missing angles for a triangle using inverse trig functions

Solving Trigonometric Equations By Factoring & By Using Double Angle Identities

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryAngle RangesEducationalMathematicsQuadrant AnalysisSine FunctionCosine FunctionTangent FunctionInverse TrigonometrySolution DiagramsMath Tutorial