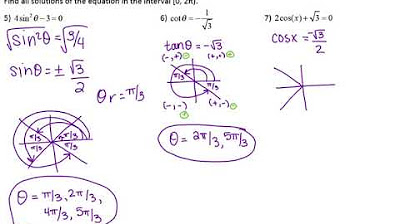Calculus AB Homework Day 2 - Review 2: Functions and Trig

Michelle Krummel

30 Aug 201728:10

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script offers a detailed walkthrough of a homework assignment focusing on function composition and trigonometry. It explains the process of evaluating composite functions for given values, using both algebraic and graphical methods. The script also covers the determination of trigonometric functions for specific angles, including quadrant analysis and the use of reference angles. Additionally, it addresses solving trigonometric equations and identifying the values of six trigonometric functions for given angles, providing a comprehensive review suitable for students.

Takeaways

📚 The video is a tutorial on a day two homework assignment focusing on the review of functions and trigonometry.
🔍 The first task involves evaluating composite functions like f(G(x)), G(f(x)), f(f(x)), and G(G(x)) for given values of x.
📉 The method demonstrated for solving composite functions is to work from the inside out, using tables for function values.
📝 For composite functions involving trigonometry, the video explains how to find exact values using the unit circle and reference angles.
📈 The video also covers evaluating composite functions using graphs, where one must find the input on the inner function's graph and then use the output as the input for the outer function.
🔢 Examples of finding composite functions for specific values like f(G(-2)), f(G(-3)), and others are given, showing step-by-step calculations.
📐 The video explains how to determine the values of functions f(x) and g(x) such that the composite H(x) = f(g(x)) holds true for given equations.
🤔 The script touches on solving trigonometric equations, such as finding angles given certain trigonometric function values, using the properties of right triangles and the Pythagorean theorem.
📉 The process of solving for angles in trigonometric equations involves understanding the signs of trigonometric functions in different quadrants and using special triangle ratios.
🔄 The video mentions the periodic nature of trigonometric functions, explaining how to find all solutions by adding or subtracting multiples of the function's period.
📝 Lastly, the script includes solving quadratic trigonometric equations by treating them as standard quadratic equations and finding the solutions for the trigonometric functions.

Q & A

What is the first problem in the video script about?
-The first problem is about evaluating composite functions f(G(x)), G(f(x)), and G(g(x)) for given values of x, starting with x = 1.
How does the script approach the evaluation of f(G(1)) in the first problem?
-The script evaluates f(G(1)) by working from the inside out, first finding G(1) which is 3, and then finding f(3) which is 5.
What is the result of G(f(1)) in the video script?
-G(f(1)) is calculated as G(4) because f(1) equals 4, and G(4) is found to be 2.
How is the value of f(f(1)) determined in the script?
-The script determines f(f(1)) by first finding f(1) which is 4, and then evaluating f(4) which gives the result of 2.
What is the process for evaluating trigonometric functions in the script?
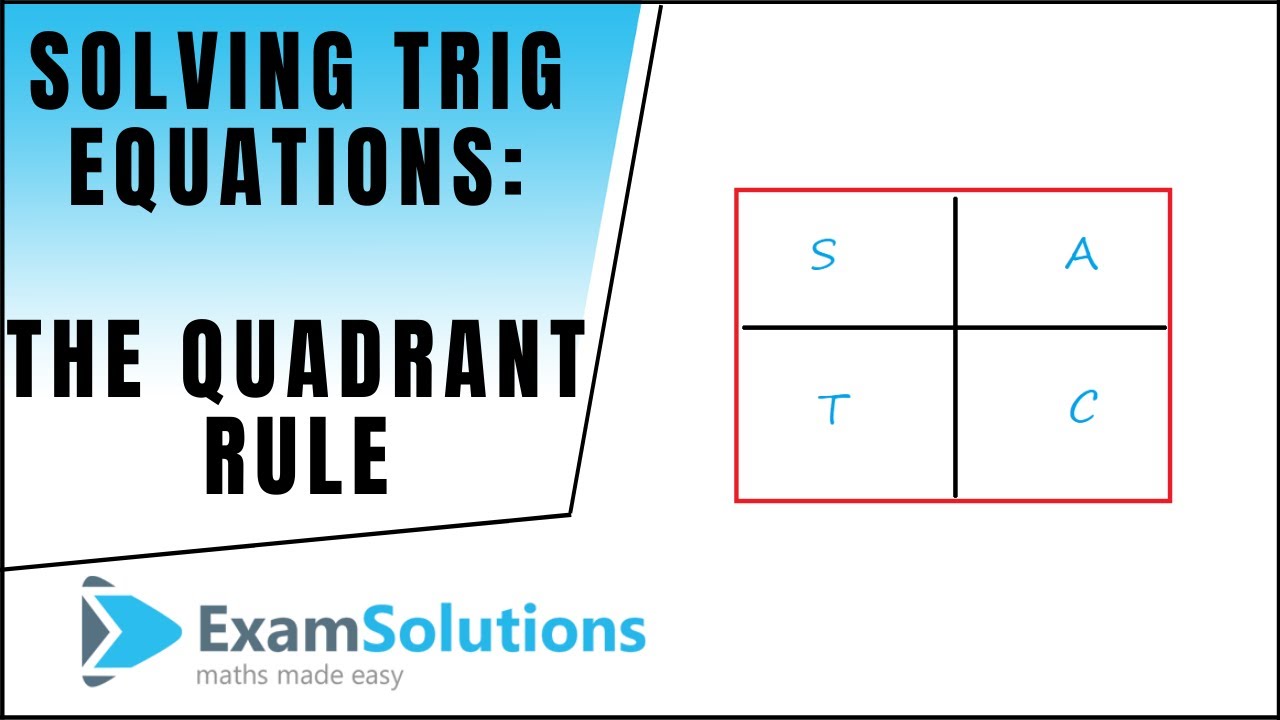
-The script evaluates trigonometric functions by identifying the quadrant the angle lies in and using reference angles along with the signs of the trigonometric functions in those quadrants.
What is the sine of 2π/3 according to the video script?
-The sine of 2π/3 is √3/2, as it is in Quadrant 2 where sine is positive.
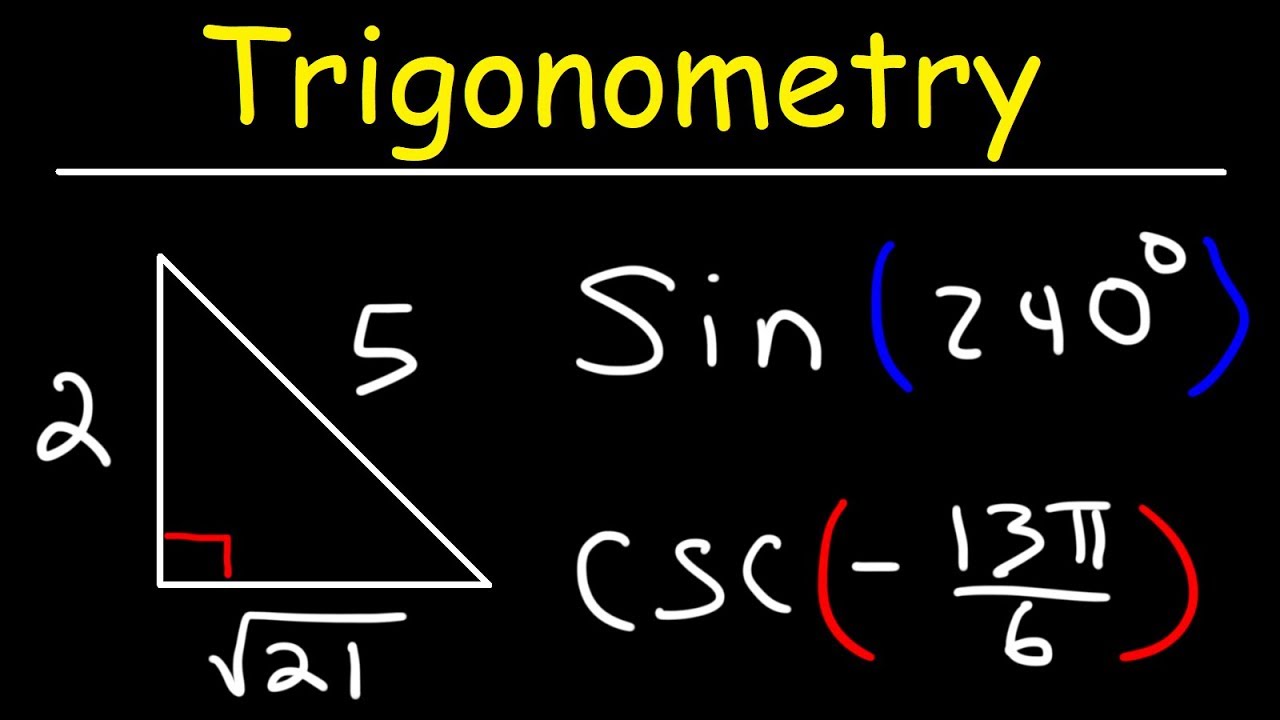
How does the script handle the evaluation of secant of π?
-The script evaluates secant of π by recognizing that the cosine of π is -1, and since secant is the reciprocal of cosine, the result is -1.
What is the approach to finding the values of trigonometric functions when θ equals arcsine(-4/9)?
-The script uses the definition of arcsine to determine that sine θ equals -4/9, then applies the Pythagorean theorem to find the remaining side of the right triangle, and uses the signs of the trigonometric functions in Quadrant 4 to find the other trigonometric values.
How does the script solve for x in the equation 2sinx + √2 = 0?
-The script isolates sinx by adding and subtracting √2, then dividing by 2, resulting in sinx = -√2/2. It then identifies the angle x where sine equals -√2/2 as 5π/4 and 7π/4, and generalizes the solution to x = 5π/4 + 2πk and x = 7π/4 + 2πk for integer values of k.
What is the solution for the equation 3tan²θ - 1 = 0 in the script?
-The script solves the equation by factoring it into (√3tanθ + 1)(√3tanθ - 1) = 0, resulting in solutions of tanθ = √3/3 and tanθ = -√3/3, which correspond to angles π/6 and 5π/6 plus multiples of π.
How does the script approach the quadratic equation in the form of 2sin²x - sinx - 1 = 0?
-The script substitutes sinx with W, resulting in a quadratic equation 2W² - W - 1 = 0, which is factored into (2W + 1)(W - 1) = 0, yielding solutions W = -1/2 and W = 1. It then translates these back to sinx, finding angles where sine is -1/2 and 1.

Outlines

00:00

📚 Composite Function Evaluation

The video script begins with an explanation of evaluating composite functions for a day two homework assignment. The instructor demonstrates how to find the values of composite functions f(G(x)), G(f(x)), f(f(x)), and G(G(x)) for given x values by working from the inside out. The process involves looking up the function tables for f and G, and calculating the results step by step. The instructor also addresses cases where the function values cannot be determined due to missing information in the tables.

05:04

📈 Evaluating Composite Functions Using Graphs

This section of the script focuses on evaluating composite functions using their graphs. The instructor explains how to determine the output values for expressions like f(G(-2)), f(G(-3)), and others by looking at the corresponding points on the graphs of the functions f and g. The process involves identifying the input values on the graphs, finding the corresponding output values, and then using those as inputs for the next function in the composite expression.

10:05

🔍 Advanced Composite Function Problems

The script continues with more complex problems involving composite functions. The instructor guides through the process of identifying inside and outside functions and composing them to form a new function H(x). Examples include finding functions f(x) and g(x) such that H(x) = f(g(x)) and solving for x in various scenarios. The approach involves understanding the composition of functions and applying the correct rules to find the solutions.

15:08

📉 Trigonometric Function Evaluations

This part of the script deals with evaluating trigonometric functions at specific angles. The instructor explains how to find the sine, cosine, secant, tangent, and other trigonometric functions for angles in different quadrants. The process includes identifying the reference angles, understanding the signs of the trigonometric functions in each quadrant, and using the reciprocal relationships between them to find the required values.

20:15

🧭 Solving Trigonometric Equations

The script presents methods for solving trigonometric equations involving arcsine and arccosine. The instructor demonstrates how to use the properties of right triangles and the Pythagorean theorem to find the values of the six trigonometric functions for a given angle. The process involves recognizing special angles, understanding the relationship between the sides of a right triangle, and applying trigonometric identities to solve for unknowns.

25:17

🔢 Solving for Angles in Trigonometric Equations

The final section of the script involves solving for angles in trigonometric equations. The instructor explains how to isolate the angle variable and find the solutions by adding or subtracting multiples of the period of the trigonometric functions involved. The process includes recognizing the periodic nature of trigonometric functions and using this property to find all possible solutions within a given range.

Mindmap

Keywords

💡Composite Functions

Composite functions are a mathematical concept where one function is applied to the result of another. In the video, the script discusses evaluating composite functions such as 'f of G of x' by working from the inside out, which means first evaluating the inner function 'G of x', and then using its result as the input for the outer function 'f'. This concept is central to the video's theme of function evaluation.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles, particularly right-angled triangles. The script covers various trigonometric functions such as sine, cosine, and tangent, and their applications in solving problems related to angles and their measurements. Trigonometry is a key theme in the video, as it is used to evaluate and solve problems involving trigonometric identities and angles.

💡Evaluation

In the context of the video, evaluation refers to the process of finding the value of a function at a specific input. The script demonstrates how to evaluate functions like 'F of G of 1' by substituting the input into the function and simplifying to find the result. This process is fundamental to understanding function behavior and is a recurring task in the video.

💡Graphs

Graphs in the video are visual representations of functions, showing the relationship between inputs and outputs. The script mentions using graphs to evaluate composite functions, such as finding 'F of G of negative 2' by looking at the output value on the graph of 'G' at the input '-2', and then using that output as the input for function 'F'. Graphs provide a visual method for understanding and solving function problems.

💡Special Trigonometric Values

Special trigonometric values refer to the exact values of trigonometric functions at specific angles, often memorized for quick reference in solving problems. The script provides examples such as the sine of 60 degrees being 'root 3 over 2' and the tangent of PI/4 being '1'. These values are essential for quickly determining the results of trigonometric expressions in the video.

💡Unit Circle

The unit circle is a circle with a radius of 1, centered at the origin of a coordinate system, and is used in trigonometry to define trigonometric functions. The script refers to the unit circle when discussing angles like '5 PI over 6' and their corresponding trigonometric values, using it as a reference for determining the signs and values of sine, cosine, and tangent in different quadrants.

💡Quadrants

Quadrants are the four equal areas created by the intersection of the x and y axes on a Cartesian plane. The script uses the concept of quadrants to determine the signs of trigonometric functions based on the angle's location. For example, in Quadrant 2, sine is positive, and cosine is negative, which is important for evaluating trigonometric expressions correctly.

💡Inverse Trigonometric Functions

Inverse trigonometric functions, such as arcsine, arccosine, and arctangent, are used to find an angle given the value of a trigonometric function. The script mentions 'arcsine of negative 4 over 9' to find an angle where the sine is '-4/9'. These functions are the reverse of the standard trigonometric functions and are used to solve for angles in various problems.

💡Pythagorean Theorem

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. The script uses this theorem to solve for the missing side of a right triangle when one side and the hypotenuse are known, as seen when finding the missing side for 'theta equals arcsine of negative 4 over 9'.

💡Reciprocal Trigonometric Functions

Reciprocal trigonometric functions are the reciprocals (inverses) of the standard trigonometric functions. The script discusses secant as the reciprocal of cosine and cosecant as the reciprocal of sine. These functions are used to find the reciprocal relationships between the sides of a right triangle and are part of the broader discussion on trigonometric identities and evaluations.

Highlights

Introduction to the video covering day two homework assignment on functions and trigonometry.

Explanation of evaluating composite functions f(G), G(f), f(f), and G(G) for given x values.

Step-by-step process for finding f(G) of 1 using function tables.

Demonstration of working from the inside out to evaluate composite functions.

Finding G(f) of 1 and illustrating the process with function tables.

Solving for f(f) of 1 and G(G) of 1 using the given function values.

Continuation of the method to evaluate composite functions for different x values.

Inability to determine f(G) of 3 due to missing function table values.

Evaluating composite functions using graphs instead of tables.

Graphical method to find f(G) of negative 2 and its output value.

Composite function evaluation using trigonometric functions and their properties.

Explanation of how to determine an f(x) and g(x) such that H(x) equals f(g(x)) with an example.

Approach to finding trigonometric values for special angles using reference angles.

Use of Pythagorean theorem to find missing sides in right triangles for trigonometric functions.

Solving trigonometric equations by transforming them into quadratic forms.

Identification of special trigonometric values for specific angles on the unit circle.

Solving for all possible solutions of trigonometric equations over different cycles.

Final solutions for the given trigonometric problems, including angles in different quadrants.

Transcripts

Browse More Related Video

Precalc 4.1-4.4 Review!

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

How to solve trigonometric equations using the Quadrant Rule

Trigonometry

Sum and Difference Identities of Sine and Cosine

Precalc Chapter 5 Review

Related Tags

Mathematics Trigonometry Composite Functions Homework Help Problem Solving Educational Content Trig Functions Right Triangles Unit Circle Inverse Trigonometry