Trigonometry: How to use the ASTC Rule | The Quadrant | CAST
TLDRThis video script offers an in-depth exploration of the Cartesian coordinate system, focusing on the concept of quadrants and their significance in trigonometry. It explains how angles are measured and categorized into four quadrants, each with specific ranges of angles from 0 to 360 degrees. The script further delves into the implications of quadrants on the signs of trigonometric functions like sine, cosine, and tangent, using a mnemonic 'All Students Take Cook' to remember which functions are positive in each quadrant. It also teaches viewers how to find the values of these functions for any angle by identifying the quadrant and reducing the angle to an acute form using specific formulas. The tutorial aims to equip viewers with the skills to solve trigonometric problems without a calculator by understanding the fundamental principles of quadrants.
Takeaways
- 📚 The video discusses the concept of quadrants in the Cartesian coordinate system, which is commonly used for graphing with x and y axes.
- 📐 Quadrants are the four regions created by the intersection of the x and y axes, each representing a quarter of the coordinate system.
- 🔢 Angles are measured in degrees, with a full circle being 360 degrees, and each quadrant representing 90 degrees.
- ⏭️ Angles are counted in an anti-clockwise direction, starting from the positive x-axis, which corresponds to 0 degrees.
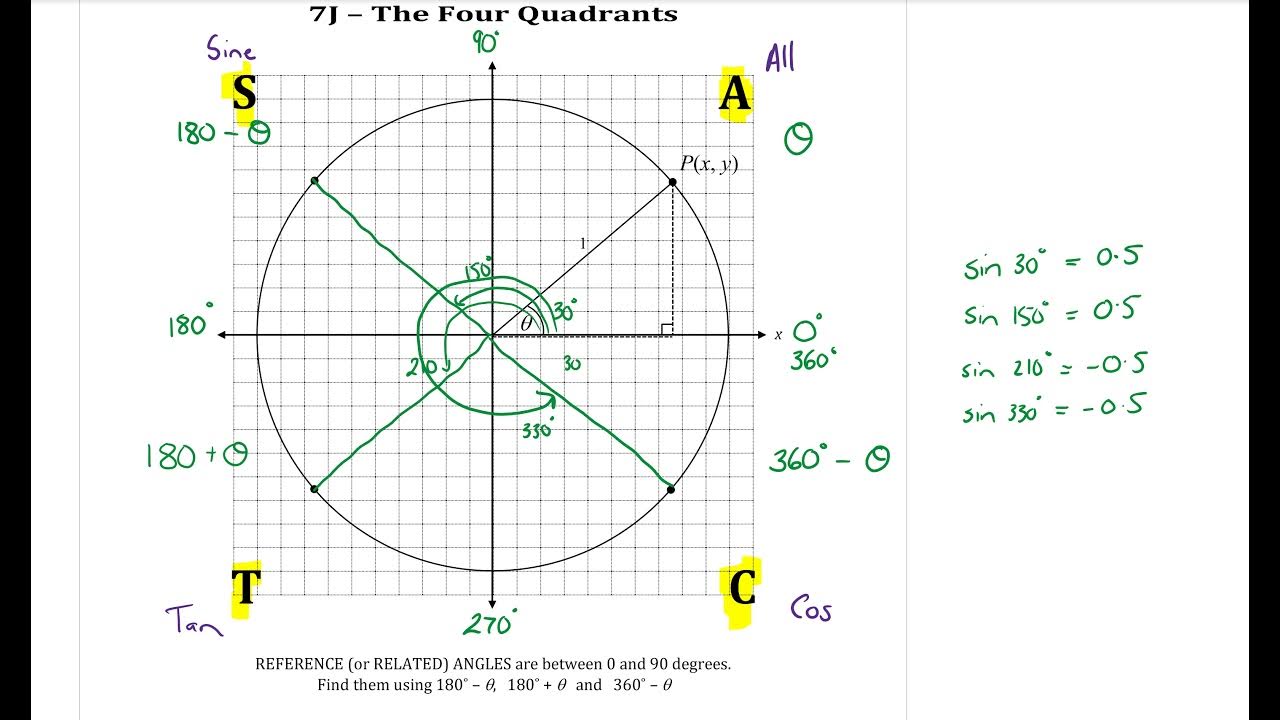
- 🧭 The first quadrant is where all angles range from 0 to 90 degrees, the second from 90 to 180, the third from 180 to 270, and the fourth from 270 to 360 degrees.
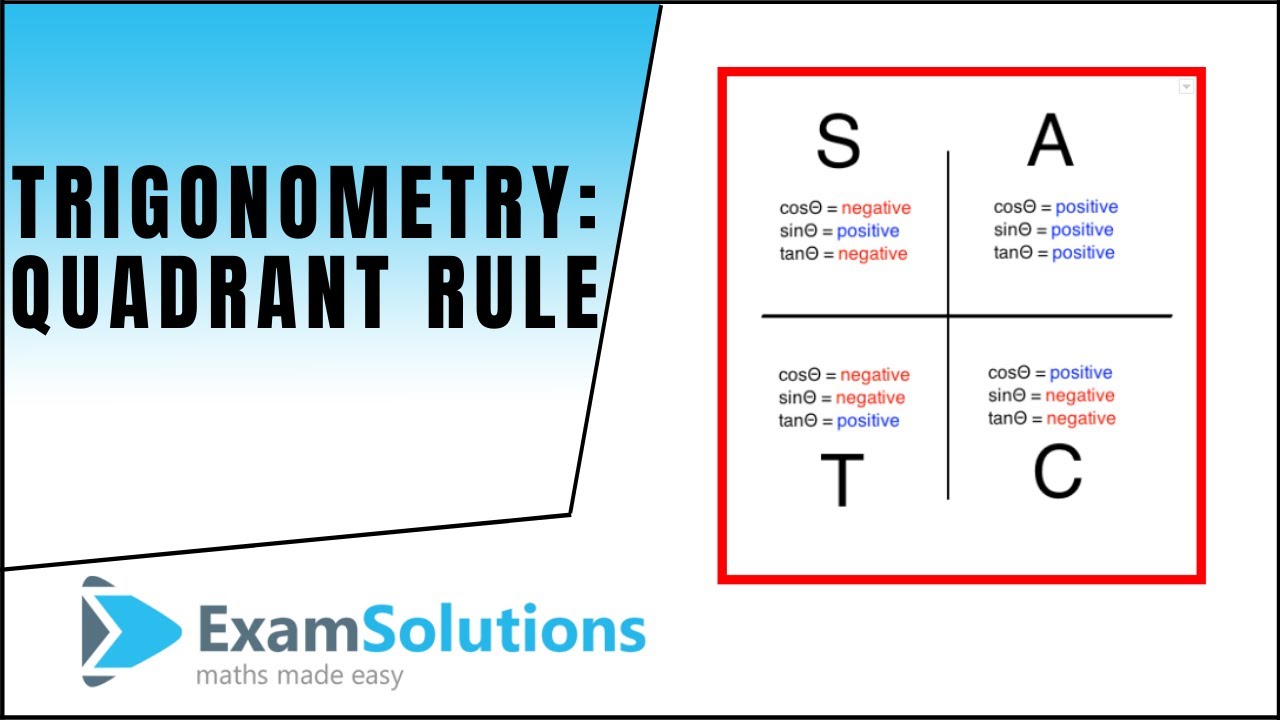
- 📈 The mnemonic 'ASTC' helps remember the signs of trigonometric functions in each quadrant: All (first quadrant), Sine only (second quadrant), Tangent only (third quadrant), Cosine only (fourth quadrant).
- 📉 In the first quadrant, all trigonometric functions (sine, cosine, tangent) are positive; in the second, only sine is positive; in the third, only tangent is positive; and in the fourth, only cosine is positive.
- 🔍 To find the value of trigonometric functions for angles not in the first quadrant, reduce the angle to an acute angle by subtracting from 180 degrees for the second quadrant, 180 degrees for the third, and adding 360 degrees for the fourth.
- 📝 Special angles like 0, 30, 45, 60, and 90 degrees have known trigonometric values, and these can be used to find the values for other angles by reducing them to these special angles.
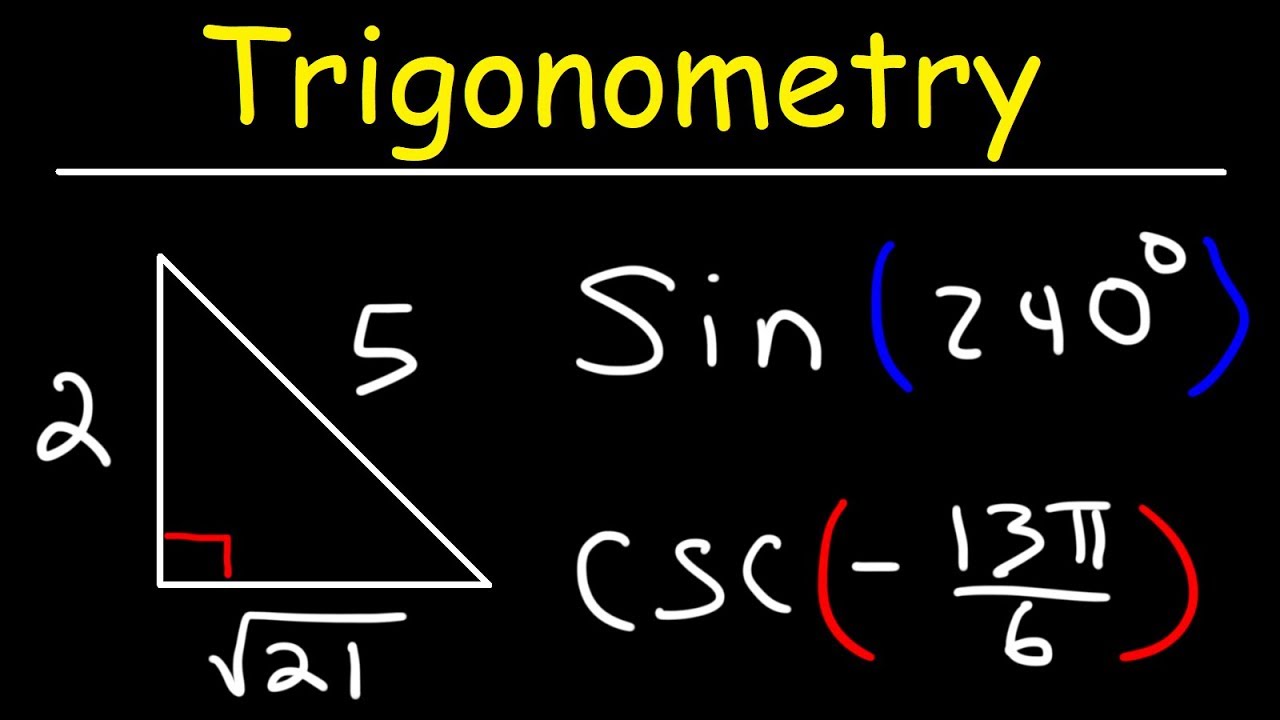
- 🔢 For example, to find sine 225 degrees, it is in the third quadrant where sine is negative, and the angle is reduced to 45 degrees by subtracting 180, resulting in a sine value of -√2/2.
- 📚 The video emphasizes the importance of understanding quadrants to solve trigonometric problems without a calculator by reducing angles and using the signs of trigonometric functions in each quadrant.
Q & A
What is the Cartesian coordinate system?
-The Cartesian coordinate system, also known as the rectangular coordinate system, is a two-dimensional coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines known as the X-axis and Y-axis.
What are quadrants in the context of the Cartesian coordinate system?
-Quadrants are the four regions into which the Cartesian coordinate system is divided. Each quadrant is one-fourth of the system, and they are numbered counterclockwise starting from the quadrant where both coordinates are positive.
How do you determine the angle between two intersecting lines?
-The angle between two intersecting lines is determined by measuring the space between them, starting from a fixed point on one line and moving to the other line. This angle can be measured in degrees, with a full revolution being 360 degrees.
What is the significance of quadrants in trigonometry?
-Quadrants are significant in trigonometry because they help determine the signs of trigonometric functions (sine, cosine, and tangent) based on the angle's position. Each quadrant has specific characteristics for these functions, which can be positive or negative.
How do you count angles in quadrants?
-Angles in quadrants are counted counterclockwise. This method aligns with the direction opposite to that of a standard clock, starting from the positive X-axis and moving through each quadrant.
What are the angle ranges for each quadrant?
-The angle ranges for each quadrant are as follows: First quadrant (0 degrees < Theta < 90 degrees), Second quadrant (90 degrees < Theta < 180 degrees), Third quadrant (180 degrees < Theta < 270 degrees), and Fourth quadrant (270 degrees < Theta < 360 degrees).
How do you determine the sign of trigonometric functions in each quadrant?
-The mnemonic 'ASTC' can be used to remember the signs: All (all three functions are positive) in the first quadrant, Sine (only sine is positive) in the second quadrant, Tangent (only tangent is positive) in the third quadrant, and Cosine (only cosine is positive) in the fourth quadrant.
What is the process for finding the sine of an angle like 315 degrees?
-To find the sine of an angle like 315 degrees, first determine the quadrant it lies in (third quadrant in this case). Then, reduce the angle to an acute angle by subtracting 180 degrees from it, which gives 135 degrees. The sine of 135 degrees can be found using known trigonometric values or a calculator.
How do you reduce an angle in the second quadrant to an acute angle?
-To reduce an angle in the second quadrant to an acute angle, subtract the angle from 180 degrees. This will give you the equivalent acute angle in the first quadrant.
What is the process for finding the cosine of an angle like 150 degrees?
-To find the cosine of an angle like 150 degrees, first determine the quadrant it lies in (second quadrant in this case). Then, reduce the angle to an acute angle by subtracting it from 180 degrees, which gives 30 degrees. The cosine of 30 degrees can be found using known trigonometric values.
Outlines
📚 Introduction to Quadrants in the Cartesian Coordinate System
The video begins with an introduction to the Cartesian coordinate system, commonly known as the rectangular coordinate system. The speaker explains the concept of quadrants, which are the four regions formed by the intersection of the positive and negative halves of the x and y axes. The video emphasizes the importance of understanding quadrants for determining the range of angles and their orientation. It also introduces the mnemonic 'All Students Take Calculus' to help remember the signs of trigonometric functions in each quadrant. The speaker provides a step-by-step explanation of how angles are measured and how they relate to the quadrants, including the process of counting angles anti-clockwise and the significance of 360 degrees as a full revolution.
🔍 Importance of Quadrants in Trigonometry and Angle Reduction
This paragraph delves into the practical application of quadrants in trigonometry, particularly when dealing with angles that are not standard or special angles. The speaker discusses how to find the sine of an angle like 315 degrees, which is not a standard angle, by using the quadrant system. The importance of quadrants is highlighted in determining whether trigonometric functions like sine, cosine, and tangent are positive or negative. The mnemonic 'All Students Take Cook' is introduced to help remember which functions are positive in each quadrant. The speaker also explains how to reduce angles in different quadrants to their acute angle components, which is essential for solving trigonometric problems without a calculator.
📘 Applying Quadrants to Solve Trigonometric Problems
The final paragraph focuses on how to use the quadrant system to solve specific trigonometric problems. The speaker provides examples of how to find the sine and cosine of angles in different quadrants, such as sine 225 degrees and cosine 150 degrees. The process of reducing these angles to their equivalent acute angles within the first quadrant is explained, allowing for the application of known trigonometric values. The speaker demonstrates how to determine the sign of the trigonometric function based on the quadrant and how to perform the reduction using simple arithmetic. The video concludes with a reinforcement of the importance of understanding and memorizing the quadrant system for solving trigonometric problems efficiently.
Mindmap
Keywords
💡Cartesian Coordinate System
💡Quadrants
💡Angle
💡Degrees
💡Trigonometric Functions
💡Special Angles
💡Mnemonic
💡Acute Angle
💡Reduction Formulas
💡Signs of Trigonometric Functions
Highlights
Introduction to the Cartesian coordinate system and its common use in graph drawing.
Explanation of quadrants as one-fourth sections of the coordinate system.
Importance of quadrants in determining the range of angles and their positions.
The concept of angles measuring the space between two intersecting lines.
Understanding a full revolution as 360 degrees and a quarter revolution as 90 degrees.
Direction of counting angles anti-clockwise in the coordinate system.
Naming and numbering of the four quadrants based on their position relative to the axes.
Identification of angle ranges for each quadrant: 0 to 90, 90 to 180, 180 to 270, and 270 to 360 degrees.
Use of quadrants to determine the signs of trigonometric functions.
Mnemonic 'All Students Take Cook' to remember the signs of sine, cosine, and tangent in different quadrants.
How to find the sine of an angle not in the list of special angles, using the quadrant system.
Method to reduce angles in different quadrants to their acute angle components.
Example calculation of sine 225 degrees using the third quadrant's properties.
Explanation of how to reduce and calculate the cosine of an angle in the second quadrant.
Practical application of quadrant knowledge in solving trigonometric problems without a calculator.
Emphasis on the importance of quadrant knowledge for identifying angles and solving trigonometric equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: