Bullet Trajectory
TLDRThis script delves into the intricacies of bullet trajectory, explaining the parabolic path influenced by various factors like projectile velocity, angle of fire, and external elements such as gravity, drag, and wind. It highlights the importance of understanding these factors for accurate shooting, introduces the concept of projectile drop due to gravity, and discusses the use of ballistics tables to predict and compensate for these effects, ensuring the bullet reaches its intended target.
Takeaways
- 📐 Trajectory is the parabolic path of a bullet from the barrel to the target, influenced by various factors.
- 👀 Line of sight and line of departure are straight lines that help compare the actual parabolic path of the bullet.
- 🚀 Internal factors like projectile velocity, spin, and angle of fire significantly affect the bullet's trajectory.
- ⏳ External factors such as gravity, drag, and wind force can alter the bullet's path and range.
- 🎯 Understanding projectile drop, the effect of gravity on the bullet's flight, is crucial for accurately zeroing a firearm's sights.
- 📊 Ballistic tables are tools used to predict a projectile's trajectory, compensating for physical effects to hit the intended target.
- 🔢 Factors like wind, temperature, air pressure, and muzzle velocity are considered in ballistic calculations.
- 📉 Projectile drop graphs illustrate the bullet's parabolic shape and help estimate where the shooter may have been based on the impact point.
- 📈 The difference in bullet velocity and projectile characteristics can cause significant changes in trajectory over long distances.
- 📚 Empirical measures are often the most reliable method for determining flight trajectories, considering the complexity of drag resistance.
- 📉 The mathematical model of drag resistance, using computation fluid dynamics, helps estimate the effects of drag on bullet flight.
Q & A
What is the trajectory of a bullet?
-The trajectory of a bullet is the path it takes from the barrel to the point it hits the target. Due to physics, this path is parabolic, meaning it is curved, even though it is often thought of as a straight line.
What are the two lines of reference mentioned in the script when discussing bullet trajectory?
-The two lines of reference are the line of sight and the line of departure. The line of sight is the straight line represented by the alignment of the front and rear sights of the firearm, while the line of departure is the straight line that runs down the center of the bore of the firearm.
How does projectile velocity affect the trajectory of a bullet?
-Projectile velocity is the most important factor affecting the trajectory's path. The speed at which the bullet travels greatly influences the distance and the degree of the curve in its parabolic path.
What are the external factors that can influence a bullet's trajectory?
-External factors that can influence a bullet's trajectory include gravity, drag, and wind force. These factors can cause the bullet to deviate from its expected parabolic path, affecting the distance and accuracy of the shot.
What is projectile drop and why is it important to understand?
-Projectile drop, also known as bullet drop, is the effect of gravity on the projectile's flight. It is important to understand projectile drop to zero the sights of a gun properly and to compensate for the drop when aiming at different distances.
How can a ballistics table help in shooting?
-A ballistics table predicts the trajectory of a projectile and is used to compensate for physical effects such as wind, drop, and other factors to increase the probability of the projectile reaching the intended target.
What does the term 'line of sight' refer to in the context of shooting?
-The line of sight refers to the straight line that is represented by the alignment of the front and rear sights of the firearm, which helps the shooter aim at the target.
How does the angle of fire affect the trajectory of a bullet?
-The angle of fire has a significant impact on the trajectory of a bullet. Different elevation angles at which the projectile is launched will result in different trajectories, affecting the range, time of flight, and the highest point of the trajectory.
What is the significance of understanding drag resistance in the context of bullet trajectory?
-Drag resistance is a factor that influences where the bullet ultimately impacts the target. Understanding and accounting for drag resistance can help in more accurately predicting the bullet's flight path and improving shooting accuracy.
How can the script's explanation of ideal projectile motion at different angles enhance a shooter's understanding?
-The script provides an example of how projectiles launched at different elevation angles will follow different trajectories. This understanding can help shooters visualize and predict the bullet's path, adjusting their aim accordingly for various shooting conditions.
What role does empirical measurement play in determining flight trajectories?
-Empirical measures often offer the most reliable method of determining flight trajectories, as they provide real-world data on how factors like drag resistance affect the bullet's path, which can be crucial for accurate shooting.
Outlines
🚀 Understanding Bullet Trajectory and Factors Influencing It
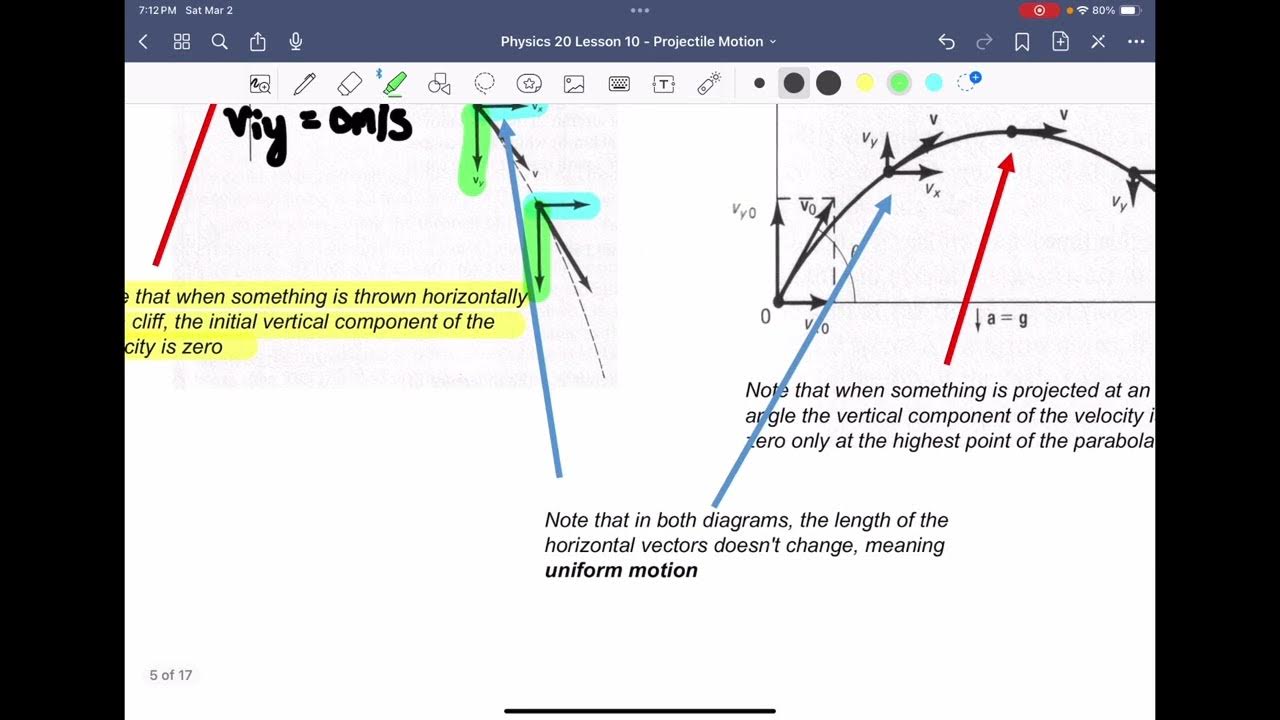
This paragraph discusses the concept of bullet trajectory, which is the parabolic path a bullet takes from the barrel to the target. It emphasizes the importance of considering the distance and various factors such as projectile velocity, spin, angle of fire, and the alignment of the firearm's sights. The paragraph also introduces the concepts of line of sight and line of departure to illustrate the bullet's actual parabolic path versus the perceived straight line. Internal factors like velocity and external factors such as gravity, drag, and wind force are highlighted as influencers of the bullet's trajectory. The impact of these factors is demonstrated through examples, showing how different trajectories can result from the same firing angle but varying conditions. The paragraph concludes with an explanation of projectile drop, which is influenced by gravity, and the importance of understanding this for zeroing a firearm's sights and compensating for bullet drop over distance.
📊 Analyzing Trajectory with Angles, Drag, and Empirical Data
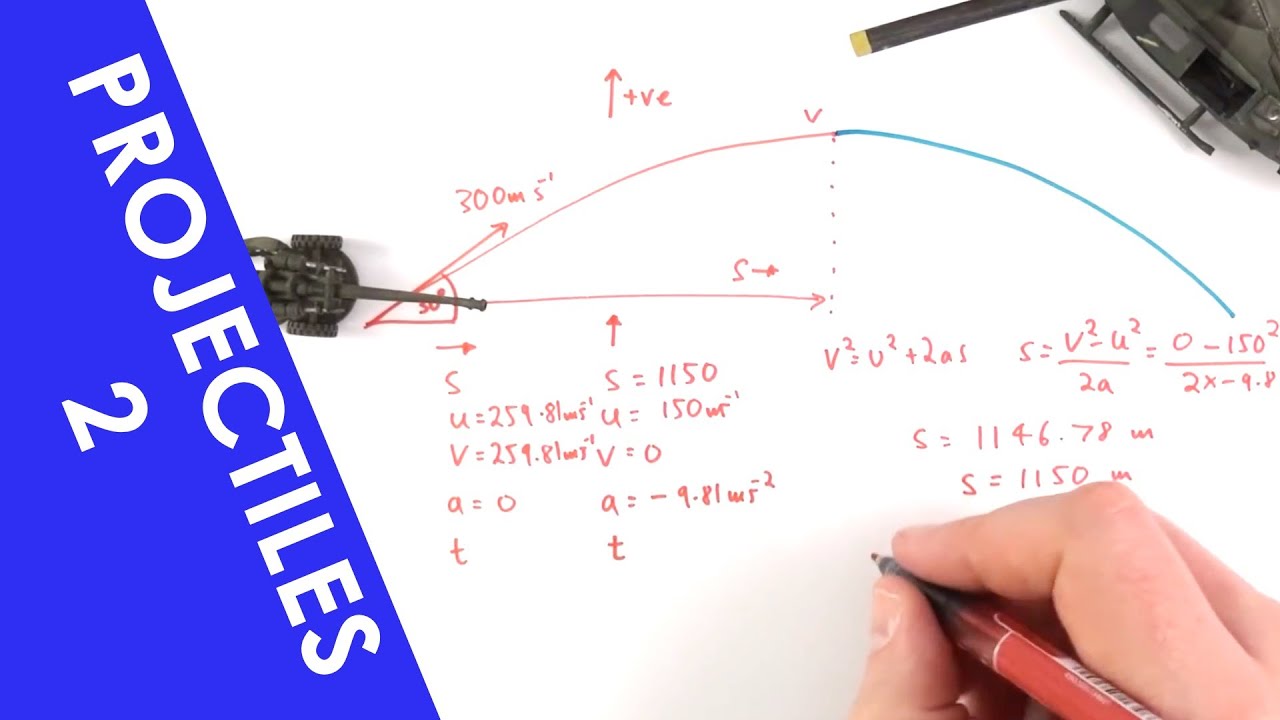
The second paragraph delves into the impact of different launch angles on projectile trajectories, using a hypothetical scenario where projectiles are launched at varying elevations with a constant speed in a vacuum with uniform gravity. The explanation includes the mathematical representation of time from launch, time of flight, range, and the highest point of the trajectory. It visually describes how the speed of the projectiles can be inferred from the length of their tails in a graph, which is represented at 0.5-second intervals. The paragraph also addresses the complexity of drag resistance, which can be estimated through mathematical models like computational fluid dynamics, but ultimately, empirical measures are often more reliable for determining flight trajectories. The importance of considering drag resistance is stressed as it significantly affects where the bullet hits the target. The paragraph concludes by emphasizing the role of empirical data in understanding the real-world impact of these factors on bullet trajectory.
Mindmap
Keywords
💡Trajectory
💡Line of Sight
💡Line of Departure
💡Projectile Velocity
💡Gravity
💡Drag
💡Wind Force
💡Projectile Drop
💡Ballistics Table
💡Drag Resistance
💡Angle of Fire
Highlights
Trajectory is the path of a bullet from the barrel to the target, influenced by various factors, and follows a parabolic curve.
Line of sight is the straight line represented by firearm sights alignment, while line of departure is the path the bullet actually travels down the bore.
The degree of bullet trajectory curve depends on factors like distance, projectile velocity, spin, and angle of fire.
External factors affecting bullet trajectory include gravity, drag, and wind force, which can significantly alter the bullet's path.
Projectile drop, or bullet drop, is the effect of gravity on the bullet's flight, important for zeroing sights and compensating for distance.
Ballistics tables predict projectile trajectory to compensate for physical effects, increasing the likelihood of hitting the intended target.
Drag resistance is a key factor in bullet flight, with empirical measures often providing the most reliable data for determining flight trajectories.
The ideal projectile motion and different launch angles are illustrated, showing how angle significantly impacts trajectory.
A vacuum and uniform downward gravity field are assumed in the mathematical model for estimating projectile motion without air resistance.
The time of flight, range, and highest point of trajectory are key parameters in understanding projectile motion at different angles.
Wind tables and drop tables in ballistics calculations help adjust for environmental factors affecting bullet trajectory.
Understanding caliber, propellant, and muzzle velocity is crucial for estimating bullet travel distance and compensating for trajectory changes.
The impact of drag factors on bullet trajectory is demonstrated, showing how they can decrease the bullet's effective range.
The effect of gravity is consistent whether a bullet is fired or simply dropped, influencing both its trajectory and drop rate.
A ballistics table is a valuable tool for shooters to compensate for various factors and improve accuracy at different ranges.
The importance of considering all factors, including air resistance and target height, is emphasized for accurate bullet trajectory prediction.
Computational fluid dynamics and other mathematical models are used to estimate the effects of drag on bullet flight, though they can be complex.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: