Deriving the 6 Basic Projectile Motion Equations

Guru Tutor
23 Aug 201912:26
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the fundamentals of projectile motion, outlining six key equations derived from constant acceleration principles, specifically the SUVAT equations, without the use of calculus. It explains the concept of a projectile, its initial velocity, and projection angle, and how these factors contribute to the trajectory. The script then methodically breaks down the motion into horizontal and vertical components, detailing how to calculate the acceleration, velocity, and displacement in both directions, and addresses the impact of gravity on the vertical motion. The inclusion of trigonometric relationships and the consideration of initial conditions, such as height from a cliff, add depth to the understanding of projectile motion. The video encourages viewers to practice deriving these equations independently for a comprehensive grasp of the subject.

Takeaways
  • πŸ“ Projectile motion involves an object moving under the influence of gravity alone.
  • πŸš€ The path of a projectile is called the trajectory, and it is influenced by its initial velocity and projection angle.
  • 🎯 The motion of a projectile can be split into horizontal and vertical components for analysis.
  • πŸ”„ Horizontal motion has zero acceleration due to the absence of horizontal forces (assuming no air resistance).
  • 🌟 The initial velocity (V naught) and projection angle (theta) are constant for a projectile.
  • πŸ“ˆ The horizontal component of the initial velocity is given by V naught times the cosine of the projection angle (V naught cos theta).
  • πŸ‹οΈβ€β™‚οΈ The vertical acceleration of a projectile is equal to the acceleration due to gravity (g), which is -9.81 m/sΒ² downwards.
  • πŸ“Š The vertical component of the initial velocity is given by V naught times the sine of the projection angle (V naught sin theta).
  • πŸ›€οΈ The horizontal displacement of a projectile is calculated using the formula: X = V naught * T * cos(theta).
  • 🏞️ The vertical displacement of a projectile is calculated using the formula: Y = V naught * T * sin(theta) - 0.5 * g * TΒ².
  • πŸ“š Understanding and being able to derive the six basic motion equations for projectile motion is crucial for solving related physics problems.
Q & A

  • What are the six basic motion equations mentioned in the transcript?

    -The six basic motion equations mentioned are derived from the constant acceleration equations, also known as the SUVAT equations, used in physics for analyzing projectile motion without the use of calculus.

  • What is a projectile in the context of the transcript?

    -A projectile, as described in the transcript, is an object that is flying through the air solely under the influence of gravity.

  • What is the significance of the projection angle (theta) in projectile motion?

    -The projection angle (theta) is significant as it defines the initial direction in which the projectile is launched. It remains constant throughout the motion of the projectile in the air.

  • How does air resistance affect projectile motion?

    -The transcript assumes no air resistance, meaning that the only force acting on the projectile is gravity. In reality, air resistance can affect the motion by reducing the object's speed and altering its trajectory.

  • What is the horizontal acceleration of a projectile in the absence of air resistance?

    -In the absence of air resistance, the horizontal acceleration of a projectile is zero because there are no horizontal forces acting on the projectile.

  • How is the initial velocity (V naught) related to its horizontal (V naught X) and vertical (V naught Y) components?

    -The initial velocity (V naught) can be split into its horizontal (V naught X) and vertical (V naught Y) components using trigonometric functions. V naught X is equal to V naught times the cosine of the projection angle (theta), and V naught Y is equal to V naught times the sine of the projection angle (theta).

  • What is the equation for horizontal displacement in projectile motion?

    -The equation for horizontal displacement (X) in projectile motion is given by X = V naught X * T, where V naught X is the horizontal component of the initial velocity and T is the time.

  • What is the acceleration acting on a projectile in the vertical direction?

    -The acceleration acting on a projectile in the vertical direction is the acceleration due to gravity (g), which is approximately 9.81 m/s^2 and is considered negative in the equations because it acts downward.

  • How can the equations for projectile motion be adjusted for a projectile launched from a height?

    -For a projectile launched from a height (H), the vertical displacement equation (y) should include an additional term of +h, representing the initial height from which the projectile is launched.

  • Why is it important to be able to derive the six motion equations on your own?

    -Being able to derive the six motion equations on your own enhances understanding and retention of the concepts. It is a valuable exercise that helps in applying these equations to solve problems related to projectile motion.

  • What is the final equation for vertical displacement in projectile motion?

    -The final equation for vertical displacement (y) in projectile motion is given by y = V naught Y * T - (1/2) * g * T^2, where V naught Y is the vertical component of the initial velocity and g is the acceleration due to gravity.

Outlines
00:00
πŸš€ Introduction to Projectile Motion

This paragraph introduces the concept of projectile motion, explaining it as the movement of an object through the air solely under the influence of gravity. It emphasizes the absence of air resistance and the importance of understanding the constant acceleration equations from physics, specifically the SUVAT equations, before proceeding. The paragraph sets the stage for the detailed explanation of projectile motion by describing a projectile's trajectory and its initial velocity and angle.

05:03
🌐 Horizontal Motion Analysis

This section delves into the analysis of horizontal motion in projectile motion. It explains that the horizontal acceleration is zero due to the absence of horizontal forces, and it uses one of the SUVAT equations to derive the horizontal component of velocity. The paragraph also discusses the initial value of velocity and breaks it down into horizontal and vertical components using trigonometric functions. The derivation leads to the first three equations of projectile motion that pertain to horizontal motion.

10:05
πŸ“‰ Vertical Motion and Equations

This paragraph focuses on the vertical aspect of projectile motion, highlighting that the only acceleration acting on the projectile is the acceleration due to gravity, which is negative in the chosen coordinate system. It provides the first equation for vertical motion, emphasizing that the gravitational constant (G) should always be positive. The paragraph then uses another SUVAT equation to derive the vertical component of velocity and displacement, leading to the last three equations of projectile motion. It also addresses the scenario where the projectile is launched from a height, adjusting the equations accordingly.

Mindmap
Keywords
πŸ’‘Projectile Motion
Projectile motion refers to the motion of an object that is propelled through the air and is influenced only by gravity. It is a type of motion where an object has an initial velocity and is launched at a certain angle, following a parabolic trajectory. In the video, this concept is central as it lays the foundation for understanding the equations and principles discussed throughout the transcript.
πŸ’‘Constant Acceleration (SUVAT Equations)
The SUVAT equations are fundamental in physics for dealing with constant acceleration motion, such as that experienced by a projectile. SUVAT stands for the four key variables: displacement (S), initial velocity (U), final velocity (V), acceleration (A), and time (T). These equations help in calculating various aspects of motion when the acceleration is constant, as is the case with projectile motion where the only acceleration is due to gravity.
πŸ’‘Initial Velocity (V_nought)
Initial velocity, denoted as V_nought in the script, is the speed at which the object is launched. It is a vector quantity, meaning it has both magnitude and direction. In the context of projectile motion, the initial velocity determines the object's speed and direction at the moment of launch, which is a critical factor in determining the trajectory and range of the projectile.
πŸ’‘Projection Angle (Theta)
The projection angle, symbolized as theta (ΞΈ) in the script, is the angle between the initial velocity vector and the horizontal direction. This angle is constant for a given projectile motion and significantly influences the trajectory of the object. The projection angle, along with the initial velocity, dictates the direction in which the object will travel.
πŸ’‘Line of Trajectory
The line of trajectory is the path followed by a projectile through the air. It is a parabolic curve that results from the combination of the object's initial velocity and the acceleration due to gravity. The line of trajectory is central to understanding projectile motion as it visually represents the motion and helps in predicting where the object will land.
πŸ’‘Horizontal and Vertical Components
In the context of projectile motion, the horizontal and vertical components refer to the separate parts of the initial velocity vector along the X (horizontal) and Y (vertical) axes. These components are crucial for analyzing the motion in two dimensions and can be calculated using trigonometric functions based on the initial velocity and projection angle.
πŸ’‘Acceleration Due to Gravity (g)
Acceleration due to gravity, denoted as 'g,' is the constant acceleration that objects experience when they fall towards the Earth. In projectile motion, it is the only acceleration acting on the object (assuming no air resistance), and it acts vertically downward. The standard value of 'g' is approximately 9.81 meters per second squared (m/s^2).
πŸ’‘Trigonometry (Cosine and Sine)
Trigonometry, specifically the use of cosine and sine functions, is essential in projectile motion to calculate the horizontal and vertical components of the initial velocity. These functions relate the angles and sides of a right triangle, which is the shape formed by the initial velocity vector and the axes when decomposing it into its components.
πŸ’‘Displacement
Displacement in the context of motion refers to the change in position of an object. It is a vector quantity that points from the initial position to the final position of the object. In projectile motion, displacement can be calculated for both horizontal and vertical directions using the derived equations, which help in determining the overall path and landing point of the projectile.
πŸ’‘Cliff Problem
The cliff problem is a specific scenario in projectile motion where the object is launched from an elevated position, such as a cliff. This introduces an initial height (h) that affects the motion of the projectile. The equations for projectile motion must be adjusted to account for this initial height, which affects the vertical displacement.
πŸ’‘Derivation
Derivation in the context of the video refers to the process of obtaining the equations of motion through logical reasoning and mathematical manipulation. It involves understanding the principles of physics and mathematics to derive the six basic equations of projectile motion, which are essential for solving problems in this field.
Highlights

Projectile motion is described by six basic motion equations derived from constant acceleration principles, also known as SUVAT equations.

In projectile motion, an object flies through the air solely under the influence of gravity, tracing out a path called the trajectory.

The initial velocity (V naught) and projection angle (theta) of a projectile are constants that do not change throughout its flight.

The motion of a projectile is split into horizontal and vertical components for analysis, using two-dimensional kinematic equations.

Horizontal acceleration of a projectile is zero, assuming no air resistance, as there are no horizontal forces acting on the object.

The horizontal component of the initial velocity (V naught X) can be found using trigonometry, specifically V naught X = V naught * cos(theta).

The horizontal displacement (X) of a projectile can be calculated using the formula X = V naught * T * cos(theta), where T is the time of flight.

The acceleration of a projectile in the vertical direction is equal to the acceleration due to gravity (g), which is -9.81 m/s^2, directed downwards.

The vertical component of the initial velocity (V naught Y) is determined by V naught Y = V naught * sin(theta), using the initial angle of projection.

The vertical displacement (Y) of a projectile is given by Y = V naught * T * sin(theta) - 0.5 * g * T^2, incorporating both initial conditions and gravitational acceleration.

Projectile motion equations can be applied to scenarios such as a projectile launched from a cliff, with adjustments to account for the initial height (H).

Understanding and being able to derive the six motion equations for projectile motion is emphasized as an essential skill, with practical applications in various fields.

The presentation of projectile motion principles avoids the use of calculus, making it accessible to a broader audience through basic physics concepts.

The importance of practice in deriving these equations independently is highlighted, as it deepens understanding and retention of the concepts.

The transcript provides a structured approach to learning projectile motion, breaking down complex ideas into manageable parts for easier comprehension.

Trigonometric functions, such as cosine and sine, play a crucial role in calculating the horizontal and vertical components of the initial velocity in projectile motion.

The concept of constant acceleration is fundamental to the analysis of projectile motion, with the acceleration due to gravity being a key factor in the vertical motion.

The transcript emphasizes the importance of correctly applying the sign convention when dealing with the acceleration due to gravity in vertical motion analysis.

The final set of projectile motion equations provided in the transcript serves as a comprehensive guide for analyzing and solving related physics problems.

Transcripts

Browse More Related Video

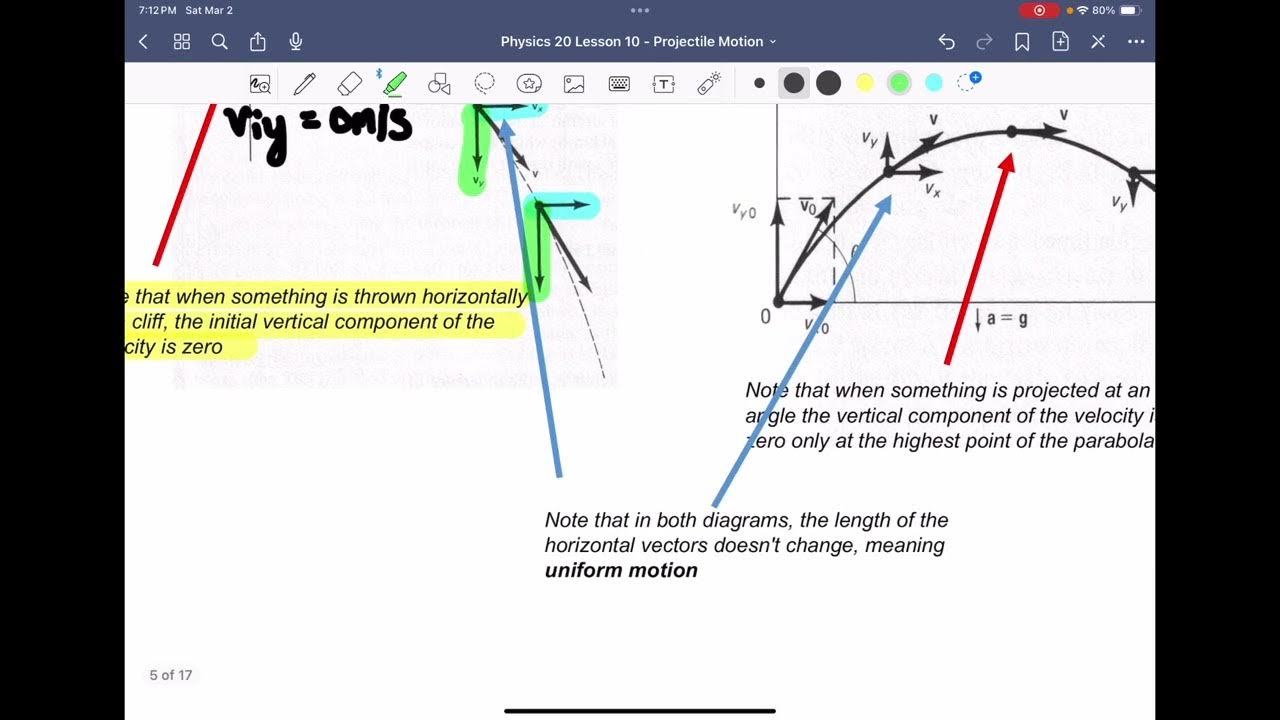
Physics 20 Unit A Lesson 10: Projectile Motion

NEET Physics | Projectile Motion | Theory & Problem-Solving | In English | Misostudy

AP Physics 1 Workbook 1.N Projectile Motion Part 2 Solution

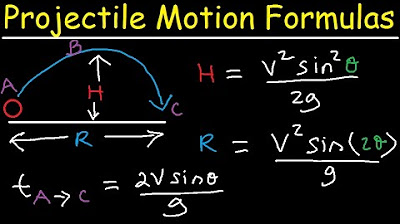
Introduction to Projectile Motion - Formulas and Equations

Projectile Motion Maximum Height Formula Derivation

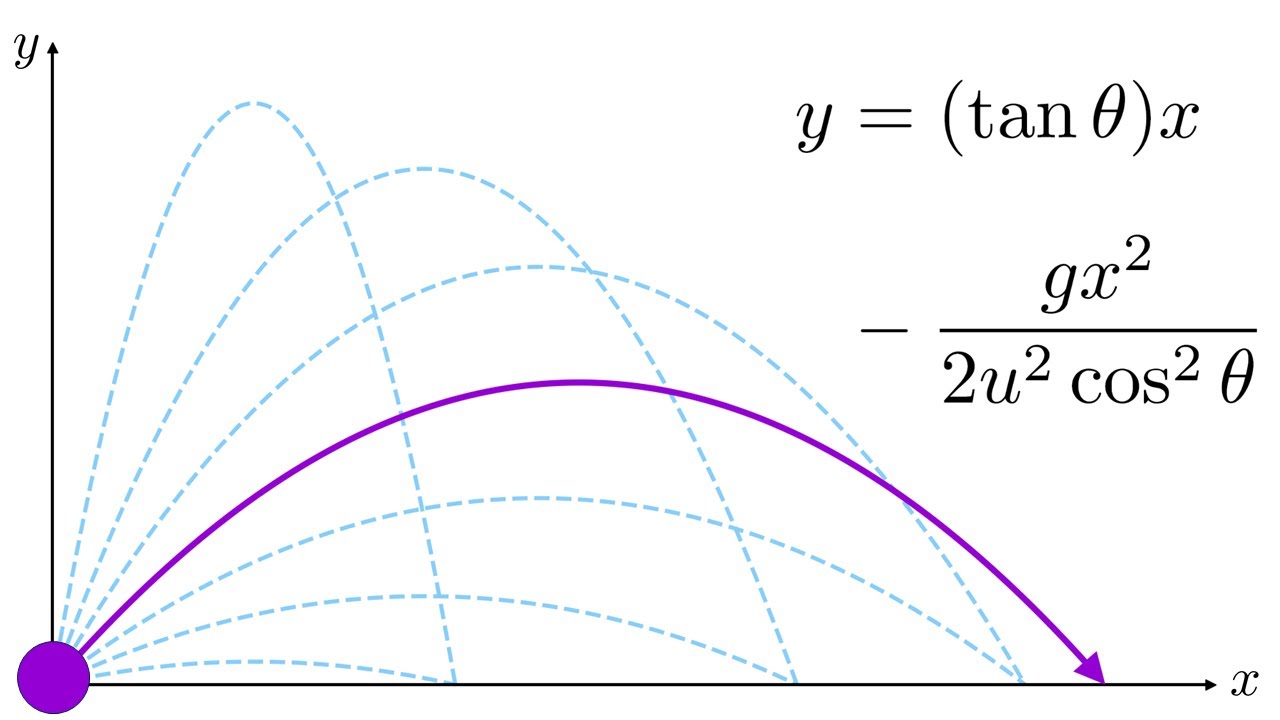
Trajectory of a projectile without drag

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationProjectileMotionConstantAccelerationSUATEquationsGravityInfluenceMotionAnalysisHorizontalVerticalComponentsTrigonometryApplicationLearningPhysicsEducationalContent