Physics 20 Unit A Lesson 10: Projectile Motion
TLDRThis educational video script covers the fundamentals of projectile motion, the final lesson in kinematics (Unit A). It recaps key concepts from previous lessons, including uniform motion, acceleration, and vector addition. The script then delves into projectile motion, emphasizing its parabolic trajectory influenced by gravity and initial velocity. It discusses various real-world scenarios, such as objects thrown horizontally or at an angle, and the importance of understanding both horizontal (uniform) and vertical (accelerated) motion components. The instructor guides viewers through several problems, illustrating how to calculate time, velocity, and displacement by integrating principles of physics, and stresses the significance of practice in mastering these concepts.
Takeaways
- 📚 The lesson is about projectile motion, which is the culmination of unit A on kinematics, integrating all previously learned skills.
- 🔍 The script provides a recap of kinematic principles, including uniform motion equations, acceleration, vector addition, and relative motion.
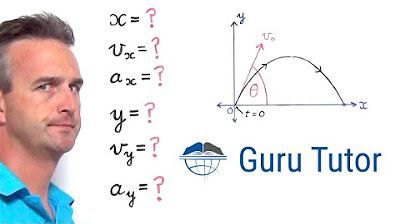
- 💥 Projectile motion is defined as the parabolic trajectory of an object in motion, influenced by gravity and initial conditions.
- 🌐 It emphasizes the importance of understanding both horizontal (uniform motion) and vertical (accelerated motion due to gravity) components in projectile motion.
- ⏱ The variable that connects the horizontal and vertical components is time, which is crucial for solving projectile motion problems.
- 🎯 The script explains that the horizontal velocity (Vx) remains constant, while the vertical velocity (Vy) changes due to acceleration by gravity.
- 📉 At the peak of projectile motion, the vertical velocity is zero, indicating the transition from upward to downward motion.
- 🔄 The principle of independence of motions is highlighted, where horizontal and vertical motions occur simultaneously but do not affect each other.
- 🧩 The script uses several examples to illustrate the process of solving projectile motion problems, emphasizing the step-by-step approach.
- 📝 It concludes with a reminder that practice is essential for mastering the concept of projectile motion and the ability to transfer information between components.
Q & A
What is the main topic of Lesson 10 in the provided transcript?
-The main topic of Lesson 10 is projectile motion, which combines all the skills discussed in the previous lessons of Unit A on kinematics.
What are the two key components of projectile motion as described in the transcript?
-The two key components of projectile motion are the horizontal component, which is uniform motion, and the vertical component, which is accelerated motion due to gravity.
Why is the horizontal velocity (VX) considered to be constant in projectile motion?
-The horizontal velocity (VX) is considered constant because there is no acceleration acting in the horizontal direction, assuming air resistance is ignored.
How does the vertical velocity (VY) change during projectile motion?
-The vertical velocity (VY) changes due to the acceleration caused by gravity. It increases in magnitude as the object falls towards the ground, and its direction is opposite when the object moves upwards after reaching the peak of its trajectory.
What is the significance of the time variable in solving projectile motion problems?
-Time is significant because it serves as the 'communicator' between the horizontal and vertical components of the motion. Solving for time in one component allows you to transfer that information to the other component.
Why do objects thrown horizontally and objects dropped from the same height hit the ground at the same time?
-They hit the ground at the same time because both objects are subject to the same acceleration due to gravity, regardless of their horizontal velocity. The horizontal velocity only affects how far the object lands from the starting point, not the time it takes to fall.
What is the formula used to relate the horizontal distance (DX), horizontal velocity (VX), and time (T) in uniform motion?
-The formula used is DX = VX * T, which states that the distance traveled in the horizontal direction is equal to the horizontal velocity multiplied by the time.
How does the initial velocity's angle of projection affect the horizontal and vertical components of the velocity?
-The angle of projection affects the horizontal and vertical components of the initial velocity through trigonometric ratios. The horizontal component is found using the cosine of the angle, and the vertical component is found using the sine of the angle.
What is the condition for the vertical velocity (VY) at the highest point of a projectile's trajectory?
-At the highest point of a projectile's trajectory, the vertical velocity (VY) is zero because the projectile momentarily stops moving upwards before it starts falling back down.
How can you determine the height of a building if a ball is thrown horizontally from the top and lands 25 meters away?
-To determine the height of the building, you would first find the time of flight using the horizontal motion (DX = VX * T), then use that time to calculate the vertical displacement (DY) using the vertical motion equations, such as DY = VIY * T + 0.5 * a * T^2, where VIY is the initial vertical velocity and a is the acceleration due to gravity.
Outlines
🚀 Introduction to Lesson 10: Projectile Motion
The instructor begins by introducing Lesson 10, which focuses on projectile motion as the culmination of Unit A on kinematics. The lesson integrates concepts from previous lessons, including uniform motion, kinematic equations involving acceleration, vector addition, and relative motion. The importance of understanding projectile motion as a combination of horizontal and vertical components is emphasized, with examples provided, such as an object thrown horizontally from a cliff or launched at an angle. Key details like initial velocities in both directions and the significance of time in solving projectile problems are highlighted.
📚 Principles of Projectile Motion and Independence of Components
This paragraph delves into the principles behind projectile motion, emphasizing the independence of horizontal and vertical components. The vertical component is influenced by gravity, resulting in accelerated motion, while the horizontal component remains uniform with no acceleration. The instructor stresses the importance of time as a common variable between the two components, which allows for the transfer of information between them. The concept of ignoring air resistance and friction in these problems is also mentioned, aligning with previous lessons.
🔍 Analyzing Projectile Motion Diagrams and Key Observations
The instructor provides a detailed analysis of projectile motion diagrams, highlighting critical observations such as the constant horizontal velocity (VX) throughout the motion and the initial vertical velocity (VIY) being zero when launched horizontally. The increase in vertical velocity (VY) as the object falls due to gravity is discussed, along with the symmetry in the motion, where velocities at the peak and on the way down are equal in magnitude but opposite in direction. The diagrams serve to illustrate these concepts and prepare students for problem-solving.
🎯 Thought Experiment: Dropped vs. Fired Bullets and Their Impact on Understanding Projectile Motion
A thought experiment is presented where a bullet is both fired horizontally and simply dropped, prompting the question of which will hit the ground first. The key takeaway is that both bullets, despite the horizontal motion of the fired bullet, will hit the ground simultaneously due to the consistent acceleration of gravity acting on both. This serves to illustrate that horizontal motion does not affect the time of flight in projectile motion, a crucial concept for understanding the independence of motion components.
📘 Projectile Motion Calculations and the Importance of Time
The paragraph outlines the process for calculating projectile motion, breaking it down into horizontal (uniform motion) and vertical (accelerated motion) components. The instructor emphasizes the importance of time as the 'universal communicator' between these components. The variables and equations necessary for solving projectile problems are introduced, highlighting the need to solve for time first, which then allows for the calculation of other unknowns.
🧩 Solving Projectile Motion Problems: A Step-by-Step Approach
The instructor provides a step-by-step guide to solving projectile motion problems, starting with an example of an object thrown vertically off a cliff. The process involves using the equations of motion to solve for time, and then using that time to calculate the horizontal speed and distance. The summary illustrates the iterative process of moving between vertical and horizontal components, using the time variable as a bridge between them.
📝 Example Problems: Applying Concepts to Calculate Horizontal Distance and Building Height
This section presents example problems that apply the concepts of projectile motion to calculate horizontal distances and the height of a building. The problems involve objects thrown off cliffs or buildings, with varying initial conditions. The solutions demonstrate the methodical approach of breaking down the problem into components, solving for time using the vertical component, and then using that time to find horizontal distances.
🏗️ Reflecting on Physics Principles and the Order of Problem Solving
The instructor reflects on the physics principles used in the previous examples and emphasizes the importance of the order in which problems are solved. Depending on the given information, one must decide whether to start with uniform or accelerated motion. The summary highlights the need for flexibility in problem-solving and the importance of understanding the principles behind projectile motion.
📐 Advanced Projectile Motion Problems: Solving with Components and Triangles
The paragraph introduces more complex projectile motion problems that require breaking down the initial velocity into its components and using trigonometric ratios. The example of a ball projected at an angle and returning to the same height is used to illustrate this process. The summary explains how to find the horizontal and vertical components, use them to determine time, and then calculate the horizontal range.
📉 Projectile Motion with Different Vertical Heights: A Cannonball Example
This section presents a scenario where a cannonball is fired at an angle from a cliff, landing at a different vertical height. The summary explains the process of breaking down the initial velocity into horizontal and vertical components, using these to find the final vertical velocity, and then determining the time of flight. Finally, it uses the horizontal component and time to calculate the landing point's horizontal distance from the cliff.
⏳ The Significance of Time in Projectile Motion and Final Thoughts
The instructor concludes by emphasizing the importance of understanding time as a critical variable in projectile motion problems. The summary reinforces the concept of passing information between the horizontal and vertical components and encourages students to practice these problems to master the material. The goal is to move beyond mere comfort with the concepts and towards true mastery, highlighting the iterative process of learning and applying projectile motion principles.
Mindmap
Keywords
💡Projectile Motion
💡Uniform Motion
💡Acceleration
💡Vector Addition
💡Free Fall
💡Kinematic Equations
💡Horizontal Displacement
💡Vertical Displacement
💡Time
💡Significant Figures
Highlights
Introduction to Lesson 10 on projectile motion, which integrates all kinematics skills discussed so far.
Recap of kinematic formulas for uniform motion and acceleration from lessons 1-9.
Explanation of projectile motion as a parabolic trajectory influenced by acceleration due to gravity.
Examples of projectile motion scenarios, including horizontal throws and launches at angles.
Clarification that initial vertical velocity (viy) is zero in horizontal projectile motion.
Emphasis on the importance of not assuming final velocity is zero in projectile motion problems.
Discussion on the independence of horizontal and vertical components in projectile motion.
Vertical motion is accelerated due to gravity, while horizontal motion remains uniform.
The principle of combined independent motions underlies the analysis of projectile motion.
Time is the variable that connects vertical and horizontal components in projectile motion problems.
Illustration of how to break down projectile motion into its components using diagrams.
Demonstration of how to calculate the time of flight and horizontal distance using kinematic equations.
Problem-solving approach where horizontal and vertical motions are solved sequentially using time as a link.
Example problem walkthroughs applying the concepts of projectile motion to real-world scenarios.
The significance of understanding the order of operations in solving projectile motion problems.
Final summary emphasizing the importance of practice in mastering the concepts of projectile motion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: