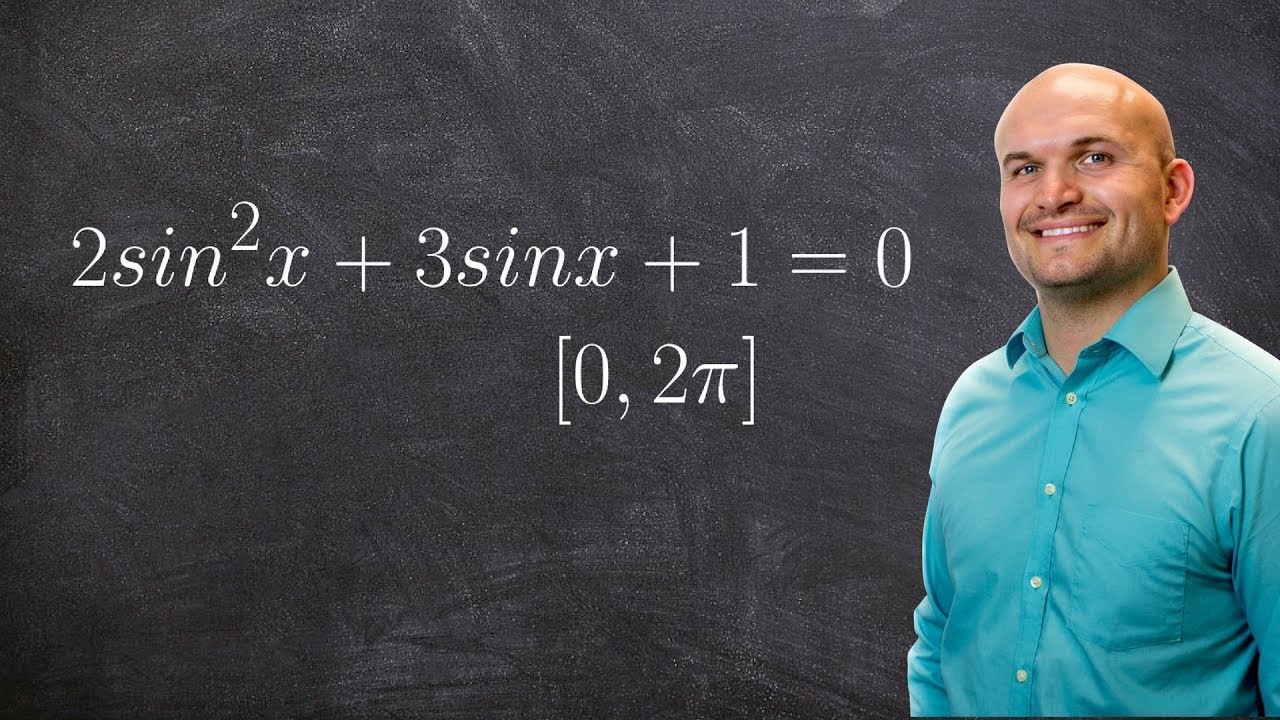Solving Trigonometric Equations By Factoring & By Using Double Angle Identities
TLDRThis educational video script focuses on solving trigonometric equations through factoring techniques. It demonstrates the process using several examples, including factoring by substitution, using the double angle formula, and the Pythagorean identity. The script emphasizes the importance of understanding the range of trigonometric functions and the difference between solving equations with trigonometric functions and their inverses, highlighting the unlimited solutions for the former and the single solution for the latter within specific ranges.
Takeaways
- 📚 The script discusses solving trigonometric equations by factoring, starting with the example of \( \sin^2 x + 2\sin x - 3 = 0 \).
- 🔍 Factoring is achieved by substitution, where \( y = \sin x \), simplifying the equation to a trinomial that can be factored into \( (y + 3)(y - 1) \).
- 📐 The solution process involves finding values of \( x \) within the first quadrant, considering the range of the sine function.
- 🧩 Another example given is \( 2\cos^2 x - \cos x - 3 \), which is factored differently due to its leading coefficient, resulting in \( (\cos x + 1)(2\cos x - 3) \).
- 🔑 The script explains that some trigonometric equations can be factored using the difference of squares formula, such as \( 4\sin^2 x - 1 = 0 \).
- 📉 The concept of the double angle formula is introduced to solve equations like \( \sin 2x = \cos x \), transforming it into a factorable form.
- 🌐 The Pythagorean identity is utilized to convert between sine and cosine functions in equations, as seen in solving \( 4\cos^2 x + 4\sin x - 5 \).
- 📝 Factoring by grouping is demonstrated in the script, where terms are grouped to simplify and factor the equation further.
- 💡 The script highlights the importance of considering the range and periodicity of trigonometric functions when solving for \( x \).
- 🚫 A cautionary note is given regarding the use of the arc sine function, which has a restricted range and does not provide the same infinite set of solutions as the sine function itself.
- 🔄 The script concludes with the understanding that while solving standard trigonometric functions can yield multiple solutions, inverse trigonometric functions typically yield a single solution within their restricted ranges.
Q & A
What is the given trigonometric equation to solve in the script?
-The given trigonometric equation to solve is sine squared plus 2 sine x minus 3 equals 0.
How does the script suggest factoring the equation involving sine squared and sine x?
-The script suggests factoring by substitution, setting y equal to sine x, and then factoring the resulting trinomial.
What are the two numbers that multiply to -3 and add up to 2 when factoring the trinomial?
-The two numbers are +3 and -1, as they multiply to -3 (3*-1) and add up to 2 (3+(-1)).
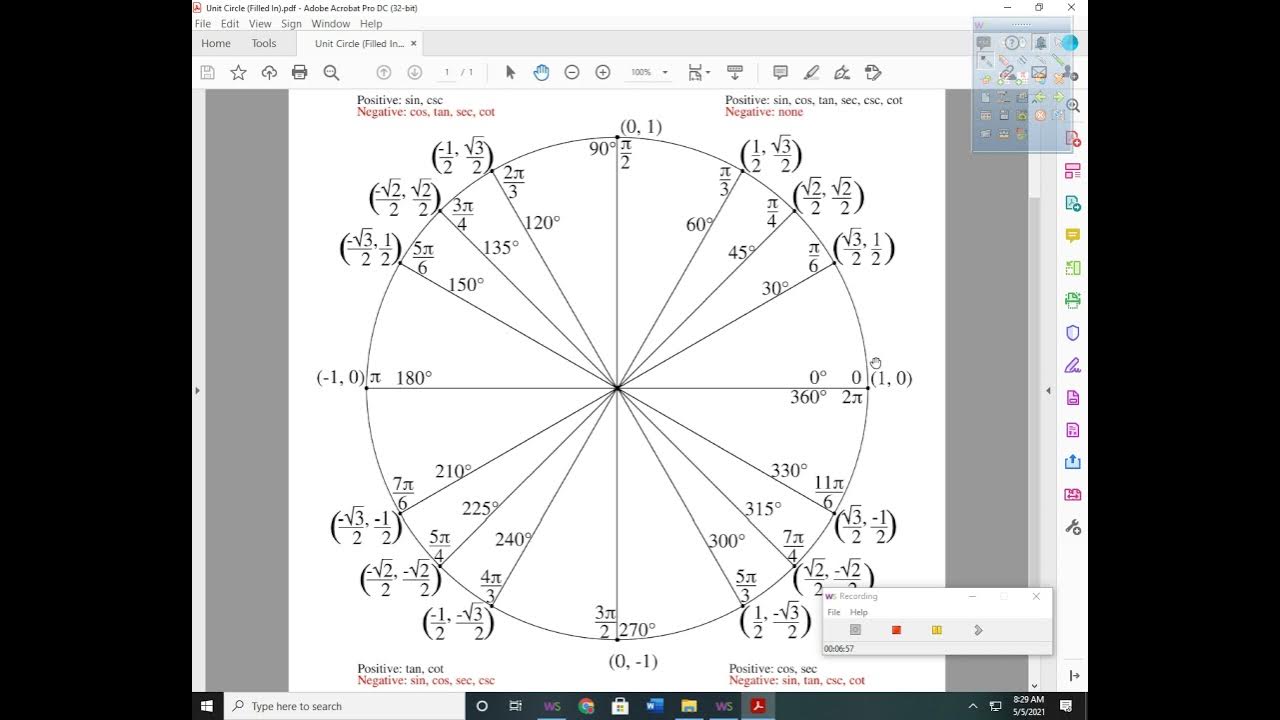
What is the range of sine x, and why can't sine x be equal to -3 in the given context?
-The range of sine x is from -1 to 1. Sine x cannot be equal to -3 because it is outside the allowable range for the sine function.
What is the solution for x when sine x equals 1?
-The solution for x when sine x equals 1 is x = pi/2, as sine of pi/2 is 1.
How does the script approach the equation involving cosine squared x and cosine x?
-The script factors the equation by grouping and then setting each factor equal to zero to find the values of x.
What is the difference between the range of sine and the range of the arc sine function?
-The range of sine is from -1 to 1 and it repeats indefinitely, while the range of the arc sine function is from -pi/2 to pi/2, and it is restricted to one solution per input within its domain.
How does the script handle the equation with sine squared minus 1?
-The script uses the difference of squares technique to factor the equation and then solves for sine x.
What are the four possible values for x when solving the equation sine squared x minus 1 equals 0?
-The four possible values for x are pi/6, 5pi/6, 7pi/4, and 9pi/4, considering the range from 0 to 2pi.
How does the script solve the equation sine 2x equals cosine x?
-The script uses the double angle formula for sine and then factors the resulting equation to find the values of x.
What is the error in simply setting x equal to the arc sine of a given value?
-The error is that the arc sine function is restricted to a specific range and does not account for all possible solutions that the sine function can have within its infinite range.
Outlines
🔍 Solving Trigonometric Equations by Factoring
This paragraph introduces the method of solving trigonometric equations through factoring. It begins with an example where sine squared plus 2 sine x minus 3 equals zero and demonstrates how to factor by substitution, setting y equal to sine x. The process involves finding numbers that multiply to the constant term and add to the middle coefficient, leading to the factored form of (sine x + 3)(sine x - 1) = 0. The solution is then found by setting each factor equal to zero, considering the range of the sine function and focusing on the first quadrant, resulting in the solution x = π/2. The paragraph also covers another example with a trinomial involving cosine, using a similar factoring approach but with a different method due to the leading coefficient, leading to the solution x = π and x = 3π.
📚 Factoring Trigonometric Equations with Pythagorean Identity
The second paragraph continues the theme of solving trigonometric equations, this time focusing on equations involving both sine and cosine functions. It discusses the use of the Pythagorean identity to simplify the equation 4 cosine squared plus 4 sine x minus 5 to zero by replacing cosine squared with 1 - sine squared. The process involves factoring the resulting trinomial and solving for sine x, which yields solutions within the range of 0 to 2π. The paragraph also addresses the difference between solving for sine and using the inverse sine function, emphasizing the infinite number of solutions for sine equations versus the single solution for inverse sine within its restricted range.
📐 Applying Double Angle Formulas in Trigonometric Equations
This paragraph delves into the use of double angle formulas to solve trigonometric equations. It presents an example where sine 2x is set equal to cosine x and shows how to apply the double angle formula for sine, transforming the equation into a factorable form. The solution process involves factoring out the greatest common factor, setting each factor equal to zero, and finding the corresponding values of x within the range of 0 to 2π. The paragraph also discusses choosing the appropriate form of the double angle formula to avoid introducing additional trigonometric functions and losing potential solutions.
🔄 Understanding the Range and Solutions of Trigonometric Equations
The final paragraph emphasizes the importance of understanding the range of solutions for trigonometric equations, especially when dealing with inverse trigonometric functions. It provides an example where sine x is equal to √3/2 and explains that while there are multiple solutions for the sine function, the arc sine function yields only one solution within its restricted range. The paragraph clarifies the difference between solving general sine equations and using inverse sine, highlighting the need to consider the function's range and the quadrant in which the solution lies.
Mindmap
Keywords
💡Factoring
💡Trigonometric Equations
💡Substitution
💡Sine and Cosine
💡Quadratic Equations
💡Double Angle Formulas
💡Pythagorean Identity
💡Range of Trigonometric Functions
💡Inverse Trigonometric Functions
💡Factoring by Grouping
Highlights
Solve trigonometric equations by factoring, starting with sine squared plus 2 sine x minus 3 equals 0.
Factor trinomials by substitution, using y equals sine x to convert sine squared to y squared.
Identify numbers that multiply to the constant term but add to the middle coefficient for factoring.
Use the factored form to set each factor equal to zero and solve for x in the first quadrant.
Cosine trinomials with leading coefficients require factoring by grouping and recognizing the greatest common factor.
Solve trigonometric equations using the difference of squares technique for expressions like 4 sine squared minus 1 equals 0.
Use the Pythagorean identity to convert between sine and cosine when they appear in the same equation.
Factor trinomials with mixed trigonometric functions by replacing one function using a Pythagorean identity.
Factor by grouping when dealing with more complex trinomials, and ensure to verify the greatest common factors.
Understand the importance of setting each factor equal to zero to solve for x in the desired range.
Apply the double angle formula for sine, recognizing that dividing by a trigonometric function may lose solutions.
Simplify and solve trigonometric equations by factoring out common terms and solving the resulting simpler equations.
Recognize solutions within the range from 0 to 2π for various trigonometric equations.
Understand the limitations and range of the arc sine function compared to the sine function for solving equations.
Use the arc sine function correctly, recognizing its range and ensuring solutions are within acceptable bounds.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: