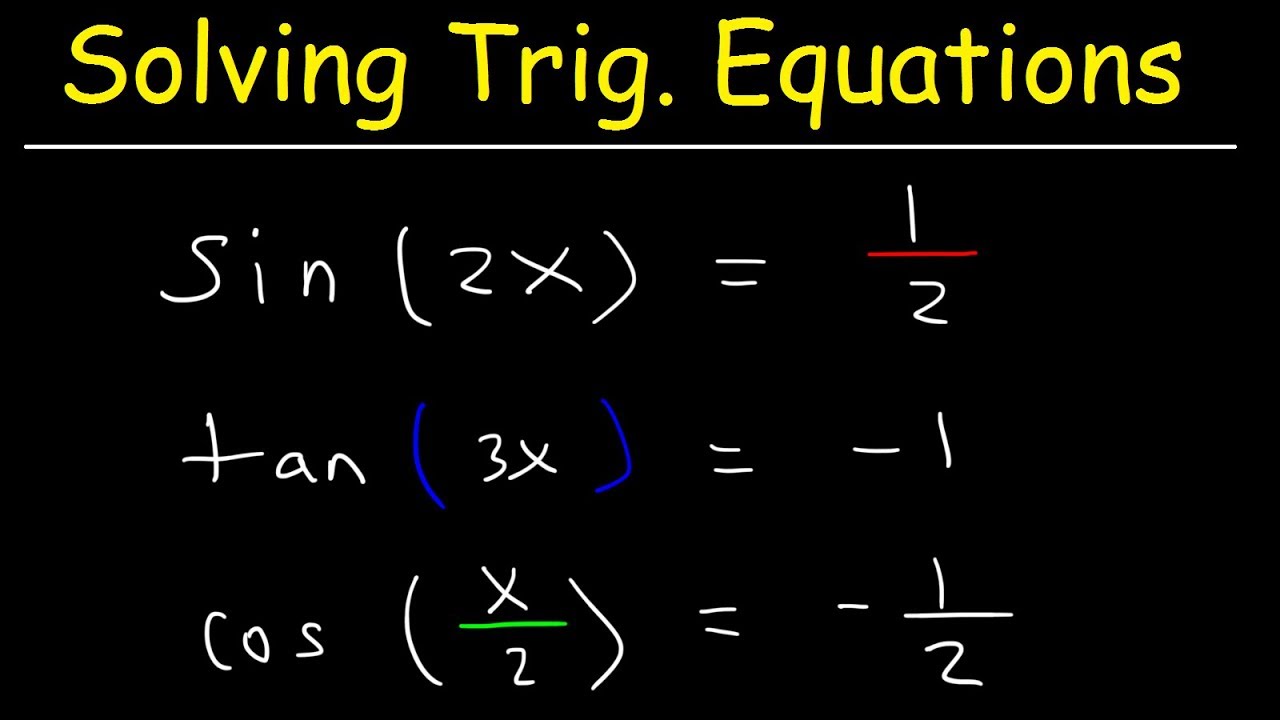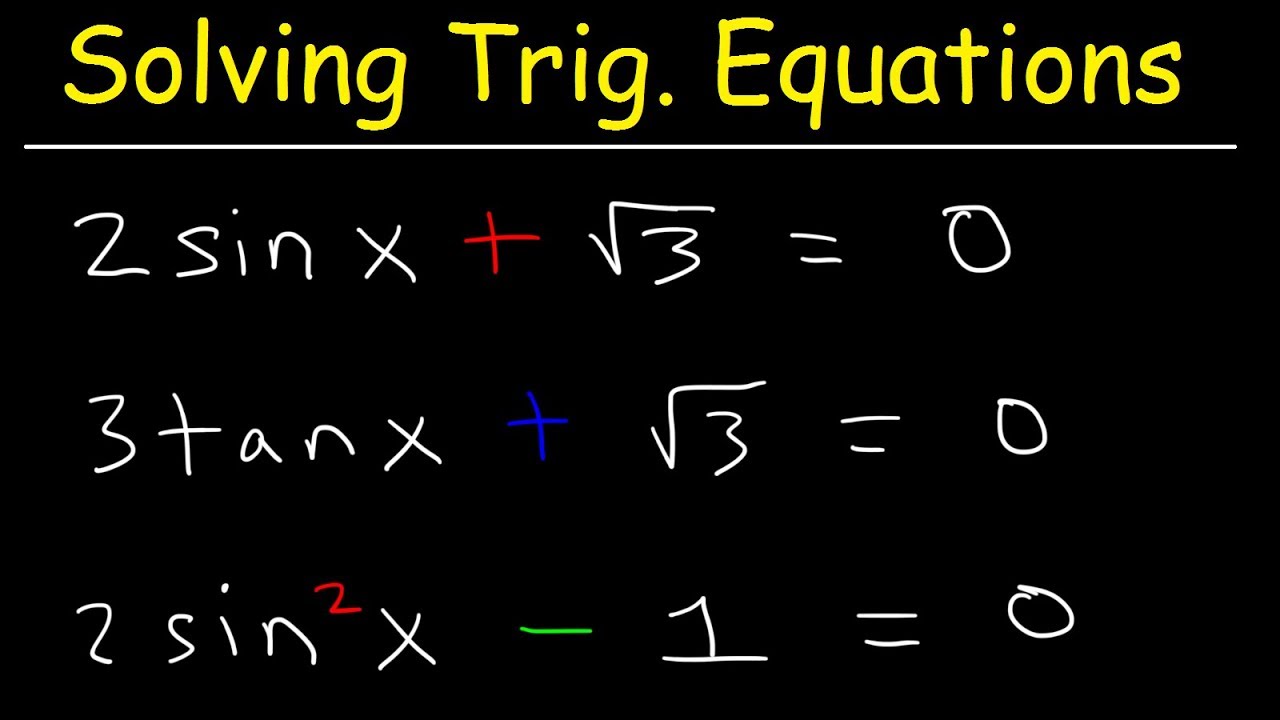Solving a trigonometric equation by factoring
TLDRThe video script is an educational walkthrough on solving algebraic equations involving trigonometric functions. It begins with a review of solving basic algebraic equations using inverse operations, such as finding the value of 'x' in '3x - 5 = 20'. The script then transitions to solving more complex equations, like '2x^2 + 3x + 1 = 0', which requires factoring and the application of the zero product property. The presenter guides the audience through the process of factoring the equation into binomials and setting each equal to zero to find the solutions. The script then applies a similar factoring technique to an equation involving sine functions, such as '2sin^2(x) + 3sin(x) + 1 = 0'. The presenter emphasizes the importance of understanding the unit circle to determine the correct angles that satisfy the equation within the interval of 0 to 2π. The video concludes with the identification of three solutions for the given trigonometric equation on the specified interval.
Takeaways
- 📐 To solve equations like 3x - 5 = 20, use inverse operations.
- 🔍 For equations with squared terms like 2x^2 + 3x + 1 = 0, factoring is required.
- 🧩 Apply the zero product property after factoring to find solutions for x.
- ✅ When factoring, look for binomials that multiply to give the quadratic expression.
- 🔢 In the example, (2x)(x) + (1)(x) = 0 leads to x = -1/2 and x = -1.
- 📉 For trigonometric equations, replace 'x' with 'sine of x' and apply similar factoring techniques.
- 🌀 Factor 2 sine^2(x) to get sine(x) and 2 sine(x), which combine to form the original expression.
- 🧮 After factoring, apply the zero product property to get sine(x) + 1 = 0 and 2 sine(x) + 1 = 0.
- 📍 Use the unit circle to find angles where sine equals -1/2 and -1.
- 🕒 The solutions for sine(x) = -1 are at x = 3π/2 and the solutions for sine(x) = -1/2 are at x = 7π/6 and x = 11π/6.
- 🔑 There are three solutions for the given trigonometric equation on the interval of 0 to 2π.
Q & A
What is the interval on which the problem needs to be solved?
-The interval on which the problem needs to be solved is from 0 to 2 pi.
What is the first step in solving a simple algebraic equation like 3x - 5 = 20?
-The first step in solving a simple algebraic equation like 3x - 5 = 20 is to use inverse operations to isolate the variable x.
Why can't we use inverse operations to solve an equation like 2x^2 + 3x + 1 = 0?
-We can't use inverse operations to solve an equation like 2x^2 + 3x + 1 = 0 because it involves a squared exponent and more than one variable, which requires factoring and the zero product property.
What property is used to solve equations that can't be solved by inverse operations alone?
-The zero product property is used to solve equations that can't be solved by inverse operations alone, particularly when dealing with factoring.
How do you factor the expression 2x^2 + 3x + 1?
-The expression 2x^2 + 3x + 1 is factored by finding two binomials whose product equals the original expression. In this case, it's (2x + 1)(x + 1).
What is the zero product property?
-The zero product property states that if the product of two factors is zero, then at least one of the factors must be zero.
How many solutions does the equation have on the interval of 0 and 2 pi?
-The equation has three solutions on the interval of 0 and 2 pi.
What are the values of x when sine of x equals negative one?
-The values of x when sine of x equals negative one are 3pi/2 and 5pi/2, which correspond to the angles on the unit circle where the sine function takes the value of -1.
What are the values of x when sine of x equals negative one-half?
-The values of x when sine of x equals negative one-half are 7pi/6 and 11pi/6, which are the angles on the unit circle where the sine function takes the value of -1/2.
How does the unit circle help in finding the solutions for sine functions?
-The unit circle helps in finding the solutions for sine functions by providing a visual representation of the sine values for different angles, making it easier to identify the correct angles that satisfy the given conditions.
What is the key difference between solving a simple algebraic equation and a trigonometric equation involving sine squared?
-The key difference is that a simple algebraic equation can often be solved using inverse operations, while a trigonometric equation involving sine squared requires factoring and the application of the zero product property.
Why is it important to know the unit circle when solving trigonometric equations?
-It is important to know the unit circle when solving trigonometric equations because it provides the relationship between angles and the values of trigonometric functions, which is crucial for determining the correct angles that satisfy the equation.
Outlines
🔍 Solving Equations with Factoring and Zero Product Property
The first paragraph introduces the process of solving equations by evaluating the sign and ensuring it falls within the interval of 0 and 2 pi. It begins with a review of solving basic linear equations using inverse operations. The speaker then transitions to more complex equations, such as quadratic ones, and explains that these cannot be solved using simple inverse operations due to the presence of a squared variable. Instead, the method of factoring is introduced, along with the zero product property, which is applied to solve the equation 2x^2 + 3x + 1 = 0. The process involves finding two binomials that multiply to give the quadratic expression and setting each factor equal to zero to find the solutions. The paragraph concludes with an example of how to apply the same factoring technique to an equation involving sine of x, resulting in two solutions for sine of x: negative one half and negative one.
📐 Applying the Unit Circle to Find Angles for Sine Values
The second paragraph focuses on applying the unit circle to determine the angles for which the sine function equals negative one or negative one half. The speaker explains that when sine of x equals negative one, the angle corresponds to 3 pi over 2, which is a basic concept on the unit circle. For sine of x equal to negative one half, the values are more complex and were previously solved as seven pi over six and eleven pi over six. The paragraph concludes by stating that there are three solutions for the given equation on the interval of 0 and 2 pi, emphasizing the importance of understanding the unit circle and its relation to the sine function.
Mindmap
Keywords
💡Solve
💡Interval
💡Inverse Operations
💡Factoring
💡Zero Product Property
💡Trigonometric Functions
💡Unit Circle
💡Sine of x
💡Algebra
💡Squaring
💡Solutions
Highlights
The transcript discusses solving algebraic equations using inverse operations and factoring techniques.
The problem-solving approach involves evaluating the sign function within the interval of 0 and 2 pi.
The transcript reviews solving a basic algebraic equation like 3x - 5 = 20 using inverse operations.
For equations with squared exponents, such as 2x^2 + 3x + 1 = 0, inverse operations are not applicable, and factoring is required.
The zero product property is applied when factoring algebraic expressions to solve for x.
The process of factoring involves guessing and checking to find binomials that multiply to zero.
When dealing with trigonometric functions, the same algebraic techniques are applied, but with sine of x and sine squared of x.
The transcript demonstrates how to factor the expression 2 sine squared of x to apply the zero product property.
The solutions to the trigonometric equation are found by setting each factor equal to zero and solving for x.
The unit circle is used to determine the angles for which the sine function equals -1 or -1/2.
The angles that satisfy the equation sine of x equals -1 are 3pi/2 and -3pi/2, which are located at the third and fourth quadrants of the unit circle.
The angles that satisfy the equation sine of x equals -1/2 are 7pi/6 and 11pi/6, which are specific points on the unit circle.
The transcript concludes with three solutions for the given trigonometric equation within the interval of 0 and 2 pi.
The importance of understanding the properties of factoring and the zero product property in solving algebraic and trigonometric equations is emphasized.
The transcript provides a step-by-step guide to solving complex equations by first simplifying them through factoring.
The method of guessing and checking is introduced as a practical approach to factoring quadratic equations.
The transcript highlights the transition from algebraic to trigonometric problems, showing the applicability of algebraic methods in different mathematical contexts.
The use of the unit circle to find the solutions for trigonometric equations is explained, tying the algebraic solutions back to geometric interpretations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: