Ch. 1.8 Inequalities
TLDRThis educational video script delves into solving inequalities, highlighting the similarities with solving equations and the crucial distinction involving the direction change when multiplying or dividing by a negative number. It covers various inequality symbols and offers a step-by-step approach to tackling linear and non-linear inequalities, including zeroing out the inequality, solving for zeros, identifying domain restrictions, and checking intervals. The script also provides clear examples to illustrate the process, emphasizing the importance of checking signs and understanding domain restrictions in rational inequalities, ultimately guiding students to find the solution sets in interval notation.
Takeaways
- 📚 Inequalities are solved similarly to equations, with the key difference being the direction change of the inequality sign when multiplying or dividing by a negative number.
- 📉 Inequalities have four symbols: strictly less than, strictly greater than, less than or equal to, and greater than or equal to.
- 🔍 Non-linear inequalities require zeroing out the inequality and analyzing the sign of the expression on either side of the zeros to determine the solution intervals.
- 🚫 When solving inequalities, it's important to identify and exclude values that are not in the domain of the equation, such as values that would make a denominator zero.
- 📉 To solve polynomial inequalities, find the zeros and check the intervals between these zeros to determine where the expression is positive or negative.
- 📝 For rational inequalities, zeroing out the inequality is recommended over clearing denominators to avoid complications with domain restrictions.
- 🔢 When checking intervals for inequalities, use simple values, and focus on the sign of the expression rather than calculating exact values.
- 🔄 Absolute value inequalities require breaking down into two cases based on the positivity or negativity of the expression inside the absolute value.
- ⚠️ Properties of absolute values are crucial when dealing with inequalities involving absolute value expressions, as they can affect the direction of the inequality.
- 📊 Graphing inequalities can help visualize the solution set, especially when dealing with complex rational or absolute value inequalities.
Q & A
What is the main difference between solving inequalities and solving equations?
-The main difference is that when you multiply or divide by a negative number in an inequality, the direction of the inequality sign changes.
What are the four symbols used in inequalities?
-The four symbols are strictly less than (<), strictly greater than (>), less than or equal to (≤), and greater than or equal to (≥).
How should non-linear inequalities be treated differently when solving?
-Non-linear inequalities should be zeroed out and then the solution should involve discussing when the expression on one side is positive or negative relative to zero.
What are the steps to solve a polynomial inequality?
-The steps include zeroing out the inequality, solving for zeros, identifying values not in the domain, and checking the values on the left and right of the zeros to determine the intervals that satisfy the inequality.
Why is it not recommended to clear denominators when solving rational inequalities?
-Clearing denominators in rational inequalities can complicate the solution by introducing squares and potentially changing the domain, which can lead to incorrect conclusions about the signs of the expression.
What is the purpose of checking values between zeros and values not in the domain when solving inequalities?
-Checking these values helps determine the intervals where the expression is positive or negative, which are crucial for constructing the solution set of the inequality.
How can you simplify the process of checking the sign of an expression in an inequality?
-Instead of calculating the exact values, you can use simple numbers and focus on the signs of the factors to determine if the overall expression is positive or negative.
What does it mean to 'zero out' an inequality?
-Zeroing out an inequality involves manipulating the inequality to have zero on one side, which simplifies the process of finding the values that satisfy the inequality.
How do you handle absolute value inequalities?
-Absolute value inequalities are handled by considering both the positive and negative scenarios of the expression inside the absolute value, effectively splitting the inequality into two separate cases.
What is the significance of the domain in solving rational inequalities?
-The domain is significant because it defines the set of permissible values for the variable. Values not in the domain, such as those that would make a denominator zero, must be excluded from the solution set.
Outlines
📚 Introduction to Solving Inequalities
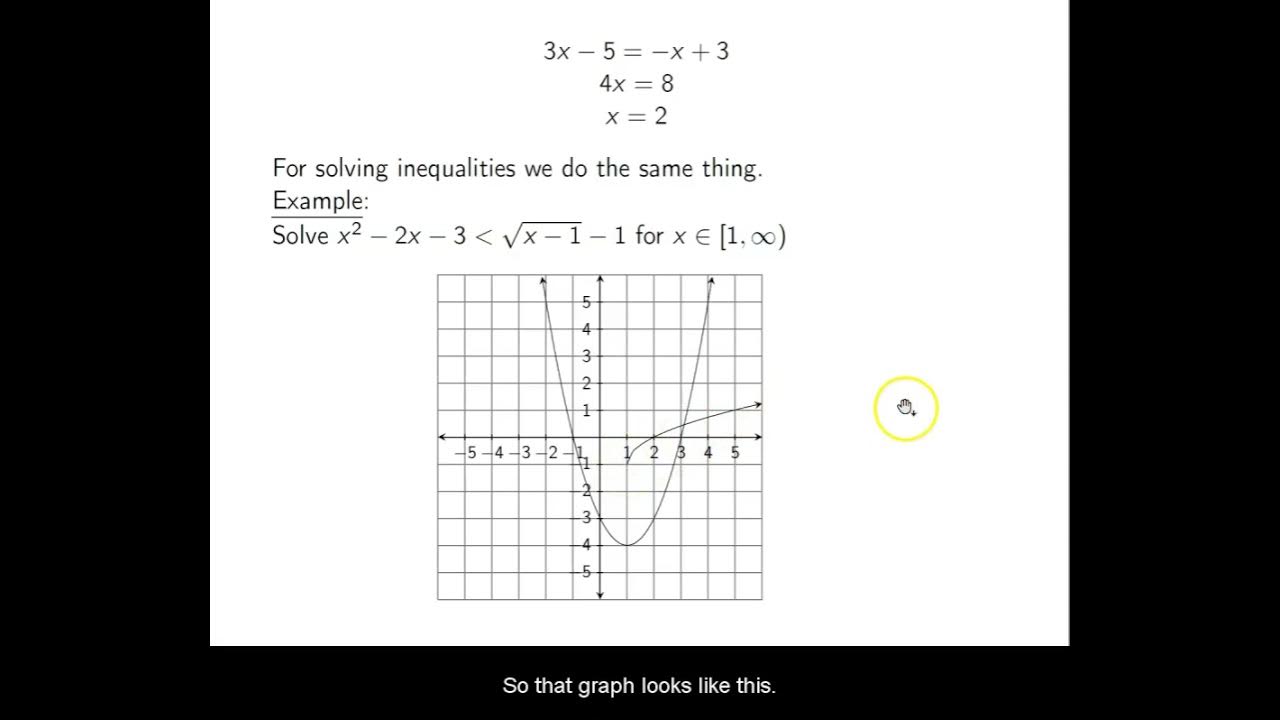
This paragraph introduces the concept of inequalities and their solution methods. It emphasizes that solving inequalities is similar to solving equations, with the key difference being the direction change when multiplying or dividing by a negative number. The paragraph explains the four inequality symbols: strictly less than, strictly greater than, less than or equal to, and greater than or equal to. It also discusses the unique approach to solving non-linear inequalities, which involves zeroing out the inequality, solving for zeros, identifying domain restrictions, and checking intervals around these values to determine the solution set.
🔍 Detailed Walkthrough of Inequality Problem Solving
The speaker provides a step-by-step guide on solving a specific inequality involving polynomials. They start by distributing and clearing denominators, then move to solving for zeros and checking intervals between these zeros. The importance of considering domain restrictions, such as values that make denominators zero, is highlighted. The process includes checking the sign of the expression at specific points to determine the intervals that satisfy the inequality. The example concludes with the solution in interval notation, including the correct handling of endpoints due to the 'less than or equal to' nature of the inequality.
📘 Rational Inequalities and Domain Considerations
In this section, the focus shifts to rational inequalities, where the speaker advises against clearing denominators due to the potential for introducing extraneous solutions. The speaker demonstrates how to zero out the inequality and combine terms over a common denominator. They identify critical values that are not in the domain, such as zeros of the denominators, and explain the process of expanding and simplifying the numerator to find zeros. The method involves checking the sign of the expression at specified intervals around these critical values to determine the solution set, taking care to exclude values not in the domain.
🔢 Solving Rational Inequalities with Checkpoints
The speaker continues the discussion on rational inequalities, detailing the process of checking the sign of the expression at values between critical points identified in the domain. They use simple values for ease of calculation and explain how to determine whether the expression is positive or negative at these points. The goal is to find intervals where the inequality holds true, excluding values not in the domain. The speaker clarifies how to interpret the signs to construct the solution set, emphasizing the importance of including or excluding endpoints based on the inequality's inclusivity.
🛑 Absolute Value Inequalities and Case Analysis
The final paragraph addresses absolute value inequalities, which require a different approach due to the dual nature of absolute values representing both positive and negative values. The speaker simplifies the expression and splits the inequality into two cases based on the definition of absolute value. They demonstrate solving these cases separately and then combine the results to find the solution set for the original inequality. The speaker also provides a list of properties for absolute values to serve as a reference for solving such inequalities. The summary concludes with the complete solution set for the example given, which spans the entire number line due to the overlapping intervals.
Mindmap
Keywords
💡Inequalities
💡Pemdas
💡Inequality Signs
💡Non-linear Inequalities
💡Domain
💡Zeroing Out
💡Quadratic Formula
💡Interval Notation
💡Rational Expressions
💡Absolute Value
Highlights
Inequalities are solved similarly to equations, with the key difference being the direction change when multiplying or dividing by a negative number.
There are four symbols for inequalities: strictly less than, strictly greater than, less than or equal to, and greater than or equal to.
Non-linear inequalities require zeroing out the inequality and discussing the positive or negative nature of the expression relative to zero.
Identifying zeros and domain restrictions is crucial for solving inequalities, especially when dealing with rational expressions or inequalities.
Checking the values on the left and right of the zeros and domain restrictions helps build the interval for the solution.
An example demonstrates solving an inequality by distributing first and then clearing denominators, leading to finding zeros and checking intervals.
For rational inequalities, it's advised to zero out the inequality without clearing denominators to avoid complications.
The process of solving rational inequalities involves identifying values not in the domain and checking the signs between these values.
An example of a rational inequality is solved by combining terms over a common denominator and checking intervals between critical values.
Absolute value inequalities require breaking down into two cases based on the positivity or negativity of the expression inside the absolute value.
Solving absolute value inequalities involves simplifying and isolating the expression, then considering the two scenarios separately.
The overlap of intervals from the two cases of an absolute value inequality can cover the entire number line.
Properties of absolute values are listed, providing a reference for dealing with single values within inequalities.
The video concludes with a summary of the process for solving inequalities, emphasizing the methodical approach to finding solution intervals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: