Solving Algebraic Inequalities
TLDRThe summary discusses inequalities in algebra. It explains that inequalities state one value is greater than or less than another, unlike equations which state two values are equal. Inequalities have many possible solutions. Solutions can be represented on a number line using open or closed circles. Inequalities can be manipulated just like equations, with one key difference: when multiplying or dividing both sides by a negative number, the direction of the inequality symbol must be reversed. This is because multiplying or dividing by a negative number inverts the number line. The summary gives examples of solving simple inequalities and notes it is done similarly to solving equations, with this one extra rule.
Takeaways
- 😀 Inequalities state that one term is greater than or less than another, unlike equations which state two terms are equal.
- 👉🏽 Inequalities have multiple solutions, while equations have one solution.
- 📐 Inequalities can be represented on number lines using open or closed circles.
- 🔢 Inequalities follow the same manipulation rules as equations.
- ❗️ Must flip inequality sign when multiplying/dividing by negatives.
- 📈 Negative numbers closer to 0 are greater than those farther from 0.
- 🪞 Multiplying by negatives inverts the number line like a mirror image.
- 🤝 Flipping inequality sign when multiplying by negatives maintains accuracy.
- 👍 Solving simple inequalities is similar to solving equations.
- 🧮 Can verify inequality flipping method by testing with whole numbers.
Q & A
What is the difference between an equation and an inequality?
-An equation sets two expressions equal to each other, while an inequality compares two expressions using greater than, less than, greater than or equal to, or less than or equal to symbols. Equations have one solution, while inequalities have multiple possible solutions.
How do you represent solutions to inequalities on a number line?
-Solutions to inequalities are shown on a number line using open or closed circles. An open circle means the endpoint is not included, while a closed circle means the endpoint is included in the solutions.
Why do you need to flip the inequality symbol when multiplying or dividing by a negative number?
-When multiplying or dividing by a negative number, the number line flips direction. To compensate for this flip, the inequality symbol must also be flipped to accurately represent the relationship between the values.
What are some examples of simple inequalities?
-Some examples of simple inequalities are: x > 3, x + 2 < 7, 3x + 4 ≥ 16, -x > 6.
How do you solve an inequality?
-Inequalities are solved using the same rules as equations. You can add, subtract, multiply, or divide both sides. The only difference is that when multiplying or dividing by a negative number, you must flip the inequality symbol.
What are some values that would satisfy the inequality x + 2 < 7?
-Some values that would satisfy x + 2 < 7 are: -5, -3, -2, -1, 0, 1, 2, 3, 4. Any value less than 5 would work.
Why is a closed circle used to represent ≥ and ≤ inequalities?
-A closed circle is used to represent ≥ and ≤ inequalities because the endpoint is included as part of the solution set. The closed circle shows the endpoint is part of the solutions.
How can a number line help explain why the inequality flips when multiplying/dividing by a negative number?
-The number line shows how multiplying/dividing by a negative number flips the direction. To keep the relationship accurate, the inequality symbol must also flip directions.
What are some practical applications of inequalities?
-Inequalities have many real-world applications like describing budgets, limits and constraints in optimization problems, or defining ranges and intervals.
What is an example of an inequality with no solutions?
-An example of an inequality with no solutions is: x + 5 < 3. No matter what number x is, when you add 5 the result will be greater than 3. So there are no values for x that satisfy this inequality.
Outlines
📝 Inequalities vs Equations
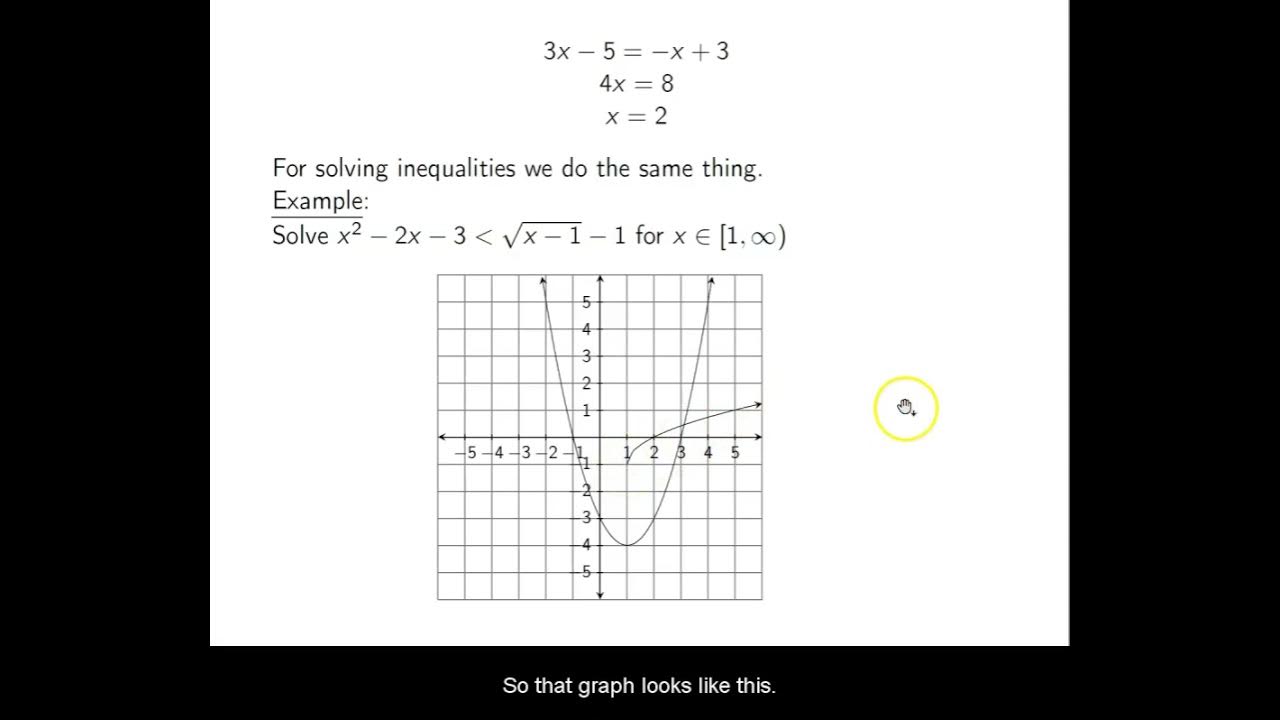
This paragraph introduces inequalities, contrasting them with equations. It explains that unlike equations where two sides are equal, inequalities state that one side is greater than or less than the other. Inequalities have multiple possible solutions rather than one precise value. Solutions are shown on a number line using open and closed circles.
😀 Solving Simple Inequalities
This paragraph shows examples of solving basic inequalities using the same manipulation techniques as equations. It covers cases with greater than, less than, greater than or equal to, and less than or equal to symbols. There is one key difference when multiplying/dividing by negative numbers - the inequality symbol must be flipped.
🧠 Understanding Inequality Symbol Flips
This paragraph provides intuition about why inequality symbols flip when multiplying/dividing by negative numbers. A number line visualization shows that this inversion mirrors and flips the line. Examples with whole numbers verify that the flip is needed for the relationship to remain accurate.
Mindmap
Keywords
💡Inequality
💡Number line
💡Solution
💡Symbols
💡Manipulate
💡Multiply
💡Divide
💡Positive numbers
💡Negative numbers
💡Verify
Highlights
First significant research finding
Introduction of new theoretical framework
Notable contribution to the field
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: