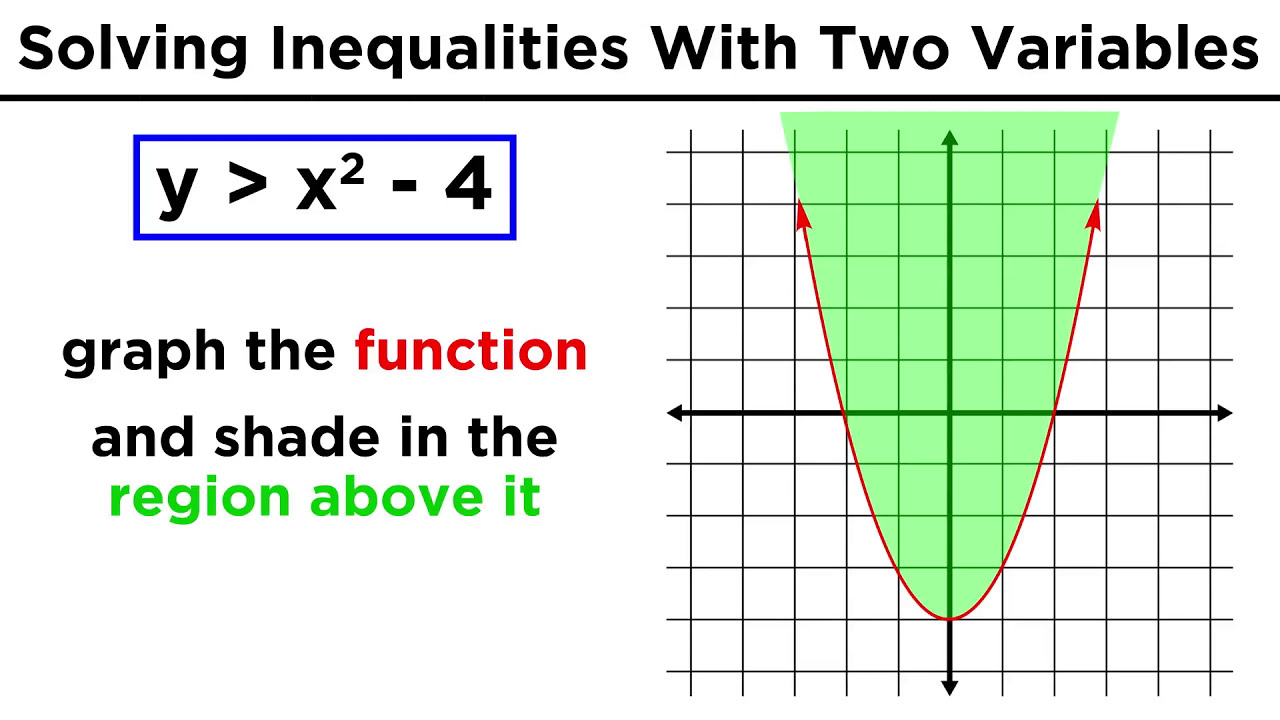
Solving Quadratic Inequalities (Precalculus - College Algebra 25)

The video begins with an introduction to quadratic inequalities, explaining what they are, their representation, and their role in mathematics. The presenter emphasizes that understanding these inequalities is crucial for future discussions on rational inequalities. A quadratic inequality is described as a mathematical statement involving a parabola and an interval where the value is either above or below a certain threshold. The process of solving these inequalities involves graphing the parabola and determining where it lies in relation to the x-axis (y=0). Key steps include moving all terms to one side of the inequality, finding the x-intercepts, and identifying the intervals where the inequality holds true.

The presenter discusses two methods for solving quadratic inequalities: graphically and algebraically. The graphical method is preferred as it aligns with future topics on rational inequalities. The process involves finding where the parabola intersects the x-axis and determining the intervals where the parabola is below the x-axis. The video explains the use of brackets and parentheses to denote whether the endpoints of the interval are included or excluded based on the type of inequality. An alternative algebraic method is also mentioned, which involves understanding the symmetry of parabolas and using truth statements to determine the solution intervals.

This paragraph delves into the process of factoring a quadratic expression to find the x-intercepts, which are crucial for interpreting the inequality. The presenter clarifies that finding the x-intercepts does not solve the inequality but provides the necessary information to determine the intervals where the parabola is above or below the x-axis. The video also illustrates how to translate the problem of a parabola being below a line into a simpler form by getting everything on one side and setting the other side to zero, which effectively turns the line into the x-axis for the purpose of the inequality.

The presenter addresses the question of downward opening parabolas and explains that the direction of the parabola's opening does not affect the solution process. Whether the parabola opens upward or downward, the method for finding the solution interval remains the same. The video demonstrates that changing the signs of the terms in the inequality and solving for an upward opening parabola yields the same interval as solving for a downward opening parabola above the x-axis. The importance of changing the inequality sign when dividing by a negative number is also highlighted.

The video continues with an example of an inequality involving a parabola and a horizontal line. The presenter shows how to manipulate the inequality to transform the problem into one where the parabola is compared to the x-axis instead of the horizontal line. Factoring the quadratic expression is key to finding the x-intercepts and determining the intervals where the parabola is above the x-axis. The use of interval notation and the decision between using parentheses and brackets based on the inequality's strictness are also discussed.

The presenter tackles a scenario where the quadratic inequality has no real solutions. This occurs when the parabola has no x-intercepts, meaning it never crosses the x-axis. The video explains how to use the discriminant from the quadratic formula to determine if there are real solutions. If the discriminant is negative, it indicates that the parabola does not intersect the x-axis, and thus there are no values for which the inequality is true. The presenter also discusses how to approach the problem if the inequality sign were changed, emphasizing that the parabola would always be above the x-axis with no x-intercepts.

In the final paragraph, the presenter concludes the discussion on quadratic inequalities and hints at future applications, including rational inequalities. The video emphasizes the importance of visualizing the parabola and the x-axis, as this approach tends to be more intuitive and memorable for students. The presenter also mentions that understanding the graphical representation of inequalities will be beneficial when dealing with more complex topics such as multiplicity and the even or odd nature of vertical asymptotes.