Calculus 3: Surface Integrals and Flux (Video #33) | Math with Professor V
TLDRThis calculus video lecture delves into the concept of surface integrals, illustrating how to integrate functions over surfaces defined by z=g(x,y) and vector fields over surfaces. It covers the partitioning of surfaces, evaluating function values at points, and the importance of the surface element ds. The lecture also explores flux, the rate of fluid flow through a surface, and demonstrates how to calculate it using the dot product of the vector field and the unit normal vector. Examples include integrating over a triangle, a helicoid, and a complex solid bounded by a cylinder and planes, highlighting the application of parametric representations and the significance of orientation in flux calculations.
Takeaways
- 📚 The lecture introduces the concept of surface integrals, which extend the idea of integrating functions over curves and vector fields to integrating functions over surfaces in three-dimensional space.
- 📐 Surface integrals are calculated by partitioning the surface into small pieces, evaluating the function at a point on each piece, multiplying by the surface increment (ds), and summing these products, taking a limit as the partition becomes finer.
- 🔍 For surfaces given by a function z = g(x, y), the surface element ds is calculated using the formula √((∂g/∂x)^2 + (∂g/∂y)^2 + 1) da, where da is a two-dimensional area element in the xy-plane.
- 📈 The surface integral of a function f over a surface s is mathematically represented as a double integral over s of f(x, y, z) ds, where z is replaced by g(x, y) if the surface is given as a function of x and y.
- 📉 The choice of coordinate plane for integration depends on the convenience in the problem, often dictated by the variables involved in the integrand and the surface equation.
- 📝 The script provides an example of integrating over a triangular surface in the xz-plane, illustrating the steps of setting up and evaluating the integral.
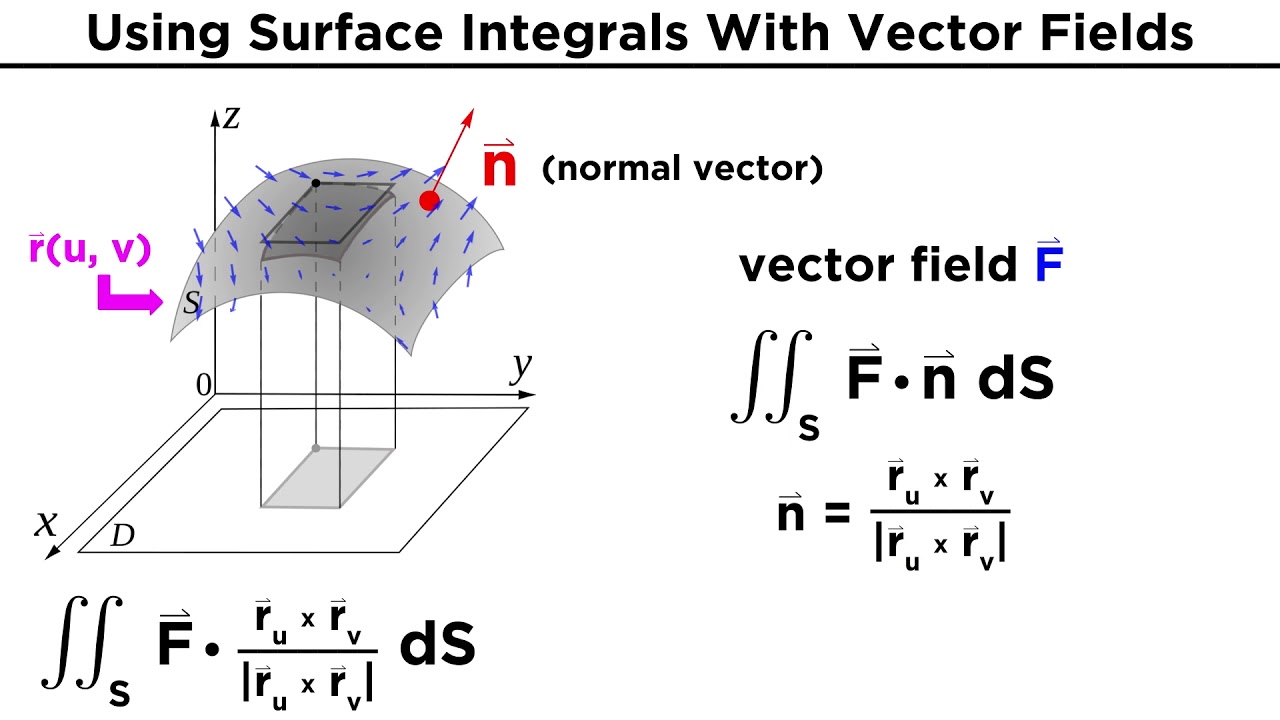
- 🌐 The concept of parametrically defined surfaces is discussed, showing how to compute surface integrals when the surface is given by a vector-valued function r(u, v) with parameters u and v.
- 🌀 The script also covers the topic of flux, which is a special case of surface integrals involving a vector field representing fluid flow, where the integral calculates the rate of flow through the surface.
- 🌡️ Flux is evaluated using the surface integral of the dot product of the vector field and the unit normal vector to the surface, representing the component of flow perpendicular to the surface.
- 🔄 The importance of surface orientation is emphasized for flux calculations, with examples provided for both upward and downward orientations and how to adjust the normal vector accordingly.
- 🎯 The final part of the script revisits an earlier example of a surface integral, this time calculating the flux of a vector field over a complex surface defined by multiple planes and a cylinder, demonstrating the process of breaking the problem into multiple integrals over different surfaces.
Q & A
What is the main topic of this calculus lecture?
-The main topic of this calculus lecture is surface integrals, which involves integrating functions over surfaces in three-dimensional space.
What is the process of integrating a function over a surface?
-The process involves partitioning the surface, picking a point in each piece, evaluating the function at that point, multiplying by the increment of surface (ds), summing them up, and taking a limit, which results in a double integral.
Why is ds considered a two-dimensional quantity when integrating over a surface?
-Ds is considered a two-dimensional quantity because it represents an increment of surface area on the surface being integrated over.
How is ds calculated when the surface is given by a function z = g(x, y)?
-Ds is calculated as the square root of the sum of the squares of the partial derivatives of g with respect to x and y, plus 1, all multiplied by da (the differential area in the xy-plane).
What is the role of the normal vector n in the context of surface integrals?
-The normal vector n is crucial for determining the orientation of the surface, especially when calculating flux, as it represents the direction perpendicular to the surface.
What is flux and how is it related to surface integrals?
-Flux represents the rate of flow of a fluid through a surface, and it is calculated by taking the surface integral of the dot product of a vector field (representing the fluid's velocity and density) with the unit normal vector to the surface.
Why is it necessary for a surface to be orientable when calculating flux?
-An orientable surface has a well-defined notion of 'up' and 'down' or 'inward' and 'outward', which is necessary to determine the direction of the flow of a fluid through the surface, which is what flux measures.
How do you determine the normal vector for a surface defined by a function z = f(x, y)?
-The normal vector for a surface defined by z = f(x, y) can be determined by taking the gradient of the function (partial derivatives with respect to x and y) and normalizing it to make it a unit vector.
What is the significance of the magnitude of the cross product of partial derivatives in a parametrically defined surface?
-The magnitude of the cross product of partial derivatives with respect to the parameters u and v gives the value of ds, the differential surface area element, which is used in the surface integral.
Can you provide an example of a non-orientable surface?
-Examples of non-orientable surfaces include the Möbius strip and the Klein bottle, which do not have a consistent orientation across their entire surface.
How does the orientation of a surface affect the calculation of flux?
-The orientation of a surface determines the direction in which the flux is calculated. If the surface is oriented 'downward', the normal vector will have a different sign than if it were 'upward', affecting the sign of the flux calculation.
What is the result of the flux calculation for the vector field x y 5 over the surface of the solid enclosed by x squared plus z squared equals one, y equals zero, and x plus y equals two?
-The total flux for the given vector field and surfaces is four pi, which is the sum of the flux through each of the three surfaces enclosing the solid.
Outlines
📚 Introduction to Surface Integrals
This paragraph introduces the concept of surface integrals, building upon the understanding of integrals of single and multiple variables over different domains. The lecture focuses on integrating a function over a surface defined by z = g(x, y), and later, the integration of a vector field over a surface. The process involves partitioning the surface into pieces, evaluating the function at a point in each piece, and summing these values over the surface area, represented by ds. The integral is set up as a double integral when the surface is expressed as a function of x and y, with ds calculated using the partial derivatives of g with respect to x and y.
📐 Calculating Surface Integrals Over a Triangle
The paragraph presents an example of calculating a surface integral over a triangular surface in the xz-plane. It begins by defining the vertices of the triangle and deriving the plane's equation, x + y + z = 1. The integrand involves x and z, prompting the choice of the xz-plane for integration. The surface is parametrized to eliminate y from the integral, and ds is expressed in terms of dx and dz. The integral is set up with appropriate limits and simplified to a double integral over the region D, resulting in the final answer of 3/24 after integration.
🧭 Surface Integrals on Parametric Surfaces
This section discusses the evaluation of surface integrals on parametric surfaces, where the surface is represented by a vector-valued function r(u, v). The integral takes the form of a double integral over the domain D, with the function f(x, y, z) replaced by its parametrized form f(r(u, v)). The magnitude of the cross product of the partial derivatives with respect to u and v gives ds for the parametrically defined surface. An example is provided where the surface is a helicoid, and the integral is set up using the parametrization of the helicoid, resulting in the final answer of 4π/3 after integration.
🏺 Integrating Over Complex Surfaces Using Multiple Integrals
The paragraph delves into integrating functions over more complex surfaces that require breaking down the surface into multiple parts for integration. An example is given where the surface is defined by the intersection of a cylinder, a plane y=0, and another plane x+y=2. The paragraph explains the process of sketching the solid and its bounding surfaces, and then setting up three separate surface integrals, one for each surface, to find the total integral over the solid.
🔍 Detailed Example of Flux Through a Paraboloid
This paragraph provides a detailed example of calculating the flux through a paraboloid defined by z = x^2 + y^2 - 9, bounded by a rectangle in the xy-plane. The flux is calculated by integrating the dot product of a given vector field with the normal vector to the surface. The vector field is adjusted to fit the paraboloid, and the normal vector is determined based on the surface's orientation. The resulting integral is simplified and evaluated over the specified region, yielding a final numerical value for the flux.
🌀 Flux Across Surfaces Defined by Parametric Equations
The paragraph explains how to calculate flux across surfaces defined parametrically, where the normal vector to the surface is found by taking the cross product of partial derivatives with respect to the parameters. The flux is then computed as the surface integral of the dot product of the vector field and the normal vector, with the integral simplified by the cancellation of the magnitude of the cross product in the ds term. An example is provided where the flux of a vector field across the surface of a solid enclosed by specific equations is calculated, resulting in a total flux of 4π.
Mindmap
Keywords
💡Surface Integrals
💡Parametric Surfaces
💡Differential Element (ds)
💡Normal Vector
💡Flux
💡Orientable Surfaces
💡Partial Derivatives
💡Vector Field
💡Permeable Surface
💡Stokes's Theorem
Highlights
Introduction to calculus 3 and the concept of surface integrals.
Explanation of integrating functions over surfaces, specifically z = g(x, y).
The process of partitioning a surface and evaluating function values at specific points.
Use of ds as a two-dimensional quantity and its relation to the increment of surface area.
Derivation of ds for a surface in the form of g(x, y) and its components.
Parametrization of surfaces and its significance in surface integrals.
Definition of the surface integral of a function f over a surface s.
Integration of functions over surfaces described as functions of x and y.
Strategy for choosing the most convenient coordinate plane for integration.
Example of evaluating a double integral over a triangular surface.
Method for finding the equation of a plane given intercepts.
Integration setup for a surface integral involving x and z variables.
Calculation of a straightforward double integral resulting in a specific value.
Discussion on the representation of surfaces using parametric equations.
Example of evaluating a surface integral over a helicoid with given parametric equations.
Introduction to the concept of flux and its relation to fluid dynamics.
Explanation of orientable surfaces and their importance in flux calculations.
Process of calculating flux using the dot product of a vector field and a unit normal vector.
Example of finding the flux of a vector field over a paraboloid surface.
Consideration of surface orientation and its effect on flux calculations.
Total flux calculation involving multiple surfaces and their respective contributions.
Transcripts
Browse More Related Video

Lec 28: Divergence theorem | MIT 18.02 Multivariable Calculus, Fall 2007
Evaluating Surface Integrals

Divergence theorem proof (part 2) | Divergence theorem | Multivariable Calculus | Khan Academy
Lec 27: Vector fields in 3D; surface integrals & flux | MIT 18.02 Multivariable Calculus, Fall 2007

Vector representation of a surface integral | Multivariable Calculus | Khan Academy

Surface integral ex3 part 3: Top surface | Multivariable Calculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: