How do you derive the period of oscillation for a pendulum?
TLDRIn this educational video transcript, the speaker discusses the challenge of deriving the formula for the period of oscillation of a pendulum, which is T = 2π√(l/g), during a GRE exam. They express concern about the complexity of pendulums in introductory physics and provide a step-by-step derivation of the formula, starting from Newton's second law and simplifying the problem for small angles. The explanation includes the use of trigonometric functions and differential equations, ultimately leading to the familiar pendulum period formula. The speaker emphasizes the importance of understanding the derivation process to better memorize and apply the formula.
Takeaways
- 📚 The script discusses the challenge of deriving the equation for the period of oscillation of a pendulum, which is a common topic in GRE physics practice problems.
- 🧭 The formula for the period of a pendulum is \( T = 2\pi\sqrt{\frac{L}{g}} \), where \( T \) is the period, \( L \) is the length of the pendulum, and \( g \) is the acceleration due to gravity.
- 🤔 The speaker expresses a dislike for the reliance on memorization of physics formulas, especially for complex concepts like pendulum motion, which are often more complicated than introductory curriculums suggest.
- 📐 The derivation of the pendulum's period begins with considering the forces acting on a mass attached to a string, including gravitational force and tension.
- 📉 The tension force is complex to calculate because both its direction and magnitude change as the pendulum swings, making direct calculation challenging.
- 🔍 The focus is on the motion constrained to the circular path of the pendulum, simplifying the problem by considering only the forces acting along the arc length.
- 📚 Newton's second law is applied in the direction of the arc length, identifying the component of gravitational force that contributes to the pendulum's motion.
- 🔄 The relationships between arc length, angular velocity, and acceleration are used to express these quantities in terms of the pendulum's angle and radius.
- 📉 For small angles, the sine of the angle can be approximated as the angle itself, simplifying the differential equation for the pendulum's motion.
- 🔍 The differential equation is solved by assuming a form for the pendulum's angular displacement as a function of time, leading to the identification of the angular frequency.
- 📐 The angular frequency is found to be \( \omega = \sqrt{\frac{g}{L}} \), which is then used to determine the period of the pendulum's oscillation.
- 💡 Understanding the derivation of physics formulas can aid in memorization and provide the ability to reproduce the formula if forgotten, emphasizing the importance of conceptual understanding over rote memorization.
Q & A
What is the equation for the period of oscillation of a pendulum?
-The equation for the period of oscillation of a pendulum is \( T = 2\pi\sqrt{\frac{L}{g}} \), where \( T \) is the period, \( L \) is the length of the pendulum, and \( g \) is the acceleration due to gravity.
Why is the derivation of the pendulum's period of oscillation difficult for introductory physics students?
-The derivation is difficult because it involves understanding the forces acting on the pendulum, dealing with variable tension, and solving a differential equation, which can be complex for students who are new to physics.
What is the significance of using the arc length 's' in the derivation?
-Using the arc length 's' allows us to apply Newton's second law in the direction of motion, simplifying the problem by focusing on the component of gravitational force that acts along the circular path of the pendulum.
What are the two forces acting on a pendulum when it is displaced from the vertical?
-The two forces acting on the pendulum are the gravitational force \( mg \) pulling straight down and the tension force in the string, which changes both in direction and magnitude as the pendulum swings.
Why is it reasonable to approximate sine theta as theta for small angles?
-For small angles, the sine function approximates linearly to the angle itself because the curve of sine theta is nearly linear near the origin. This simplification makes the differential equation easier to solve.
What is the relationship between angular velocity (ω) and the radius (r) of the circle in the context of circular motion?
-The relationship is given by \( v = r\omega \), where \( v \) is the linear velocity, \( r \) is the radius of the circle, and \( \omega \) is the angular velocity.
How does the angular acceleration (α) relate to the second derivative of the angle with respect to time?
-The angular acceleration is the second derivative of the angle with respect to time, which means \( \alpha = \frac{d^2\theta}{dt^2} \).
What is the differential equation derived for a pendulum's motion when considering small angles?
-The differential equation for a pendulum's motion under the small angle approximation is \( \theta'' = -\frac{g}{L}\theta \), where \( \theta'' \) is the second derivative of the angle with respect to time.
What function can you assume for θ(t) to solve the differential equation of a pendulum's motion?
-You can assume a function of the form \( \theta(t) = A\cos(\omega t) + B\sin(\omega t) \), where \( A \) and \( B \) are constants, and \( \omega \) is the angular frequency.
How is the angular frequency (ω) related to the period (T) of the pendulum's oscillation?
-The angular frequency is related to the period by the equation \( \omega = \frac{2\pi}{T} \), which can be rearranged to solve for the period as \( T = 2\pi\sqrt{\frac{L}{g}} \).
Why is understanding the derivation of a formula beneficial for remembering it?
-Understanding the derivation provides a deeper insight into the formula's components and their relationships, making it easier to memorize and recall, as well as to reproduce if forgotten.
Outlines
🤔 Deriving the Pendulum Period Equation
The speaker addresses a problem encountered during GRE practice related to the period of oscillation for a pendulum. They express dissatisfaction with such questions on the GRE due to the difficulty in deriving the equation quickly. The speaker mentions a preference for not including pendulums in introductory curricula because of their complexity. They proceed to derive the equation for the period of a pendulum's oscillation in a manner they believe would be easiest for introductory students to understand. The setup involves a mass on a string of length L pulled at an angle θ, with gravitational force mg acting downward and tension in the string. By focusing on motion constrained to a circular path and using Newton's second law, they derive the necessary components to explain the period equation.
📐 Simplifying the Derivation for Small Angles
The speaker continues the derivation by considering the scenario where the angle θ is small. They explain that for small angles, sin(θ) can be approximated by θ, simplifying the equation. Using this approximation, they rewrite and solve the differential equation for θ and its second derivative. They explore the relationship between angular quantities and their derivatives, identifying that the solution involves trigonometric functions. By assuming θ(t) as a combination of cosine and sine functions, they derive the angular frequency ω and subsequently the period T of the pendulum. The speaker emphasizes that understanding the derivation process helps in memorizing the equation and potentially reproducing it when needed. They conclude by noting the time-consuming nature of such derivations in test settings like the GRE.
Mindmap
Keywords
💡Period of Oscillation
💡Pendulum
💡Newton's Second Law
💡Arc Length
💡Gravitational Force
💡Tension
💡Small Angle Approximation
💡Differential Equation
💡Angular Acceleration
💡Simple Harmonic Motion
Highlights
Derivation of the pendulum period equation from first principles is challenging, especially under time constraints like the GRE.
The speaker prefers not to memorize equations but to understand their derivation for better retention.
Introduction to the problem of deriving the period of oscillation for a pendulum without the formula.
Explanation of the forces acting on a pendulum: gravitational force and tension.
The complexity of calculating tension due to its changing direction and magnitude.
Using Newton's second law in the arc length direction to simplify the problem.
Relating arc length, velocity, and acceleration to angular quantities.
The assumption that for small angles, sine theta can be approximated by theta itself.
Formulation of the differential equation for the pendulum's motion.
Solving the differential equation by guessing a trigonometric function form for theta(t).
Deriving the relationship between angular frequency and the physical parameters of the pendulum.
The importance of understanding the derivation process for better memorization of equations.
The speaker's opinion on the complexity of pendulums in introductory physics curriculum.
The process of taking the second derivative to find the relationship with the original function.
The final derivation of the pendulum's period equation T = 2π√(l/g).
The practical difficulty of deriving this equation under the time pressure of a GRE exam.
The speaker's approach to teaching and learning physics, emphasizing understanding over memorization.
Transcripts
Browse More Related Video
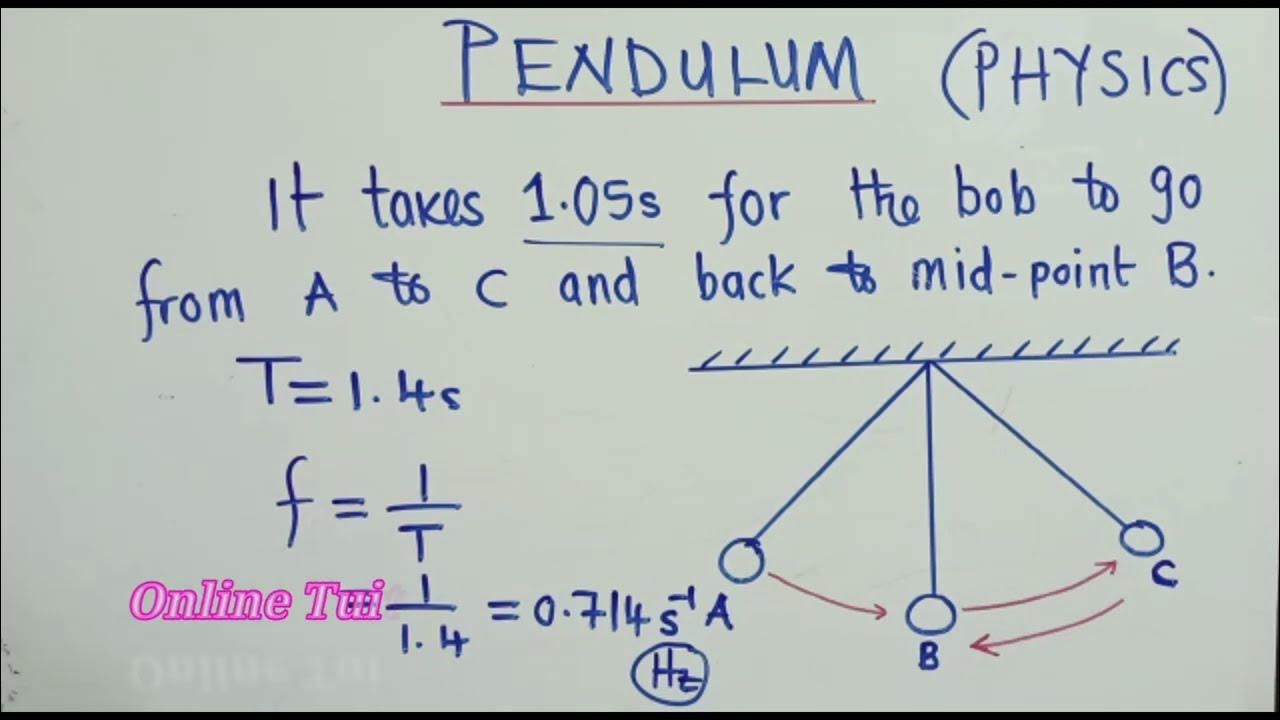
Physics-Pendulum exam question

Simple Harmonic Motion - Physics 101 / AP Physics 1 Review with Dianna Cowern

Pendulums | Oscillations and mechanical waves | Physics | Khan Academy

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion
The Simple Pendulum
Half Angle Formulas & Identities - Evaluating Trigonometric Expressions
5.0 / 5 (0 votes)
Thanks for rating: