Lec 27: Vector fields in 3D; surface integrals & flux | MIT 18.02 Multivariable Calculus, Fall 2007

MIT OpenCourseWare

27 Jan 200950:34

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture delves into the concept of vector fields and flux in three-dimensional space, introducing the idea of flux as a surface integral rather than a line integral. The instructor discusses the setup of triple integrals in various coordinate systems and explores examples including gravitational and electric fields. The focus then shifts to calculating flux through surfaces like spheres and cylinders using parameters such as phi and theta, highlighting the importance of choosing an orientation for the surface and the normal vector. The lecture concludes with a look ahead to the divergence theorem and more complex plane scenarios.

Takeaways

📚 The lecture discusses the concept of vector fields in space and their applications, emphasizing the importance of understanding flux and work in physics and mathematics.
🌌 A vector field in space is represented by a vector at every point, with components that depend on the coordinates x, y, and z, and can be visualized in terms of direction and magnitude.
🔍 The script provides examples of vector fields, such as gravitational attraction and electric fields, which are directed towards the origin with magnitudes inversely proportional to the square of the distance from the origin.
🌀 The concept of flux is introduced as a measure of how much a vector field crosses a surface, transitioning from line integrals in 2D to surface integrals in 3D.
📏 The normal vector's role in flux calculations is highlighted, with the need to choose an orientation for the surface to determine the direction of the normal vector.
📉 The script explains how to calculate flux through a surface by setting up a double integral, which involves reducing three variables to two by understanding the surface's geometry.
🔄 The importance of the dot product in flux calculations is emphasized, as it isolates the normal component of the vector field that contributes to the flux.
📘 Two examples of calculating flux are provided: one with a vector field radiating away from the origin through a sphere, and another with a vector field perpendicular to a sphere's surface.
📐 The use of spherical coordinates (phi and theta) for setting up surface integrals on a sphere is introduced, along with the formula for the surface element dS in these coordinates.
📊 The script demonstrates how to compute flux through a sphere for different vector fields, using geometric arguments and integration techniques.
📚 The importance of learning to set up double integrals for surfaces is stressed, as it is a fundamental skill for solving flux problems in various geometries.

Q & A

What is the purpose of the support mentioned in the script for MIT OpenCourseWare?
-The support mentioned is intended to help MIT OpenCourseWare continue to offer high-quality educational resources for free.
What are triple integrals and how are they used in the script?
-Triple integrals are a mathematical concept used to integrate functions of three variables over a three-dimensional region. In the script, they are discussed in the context of setting them up in various coordinate systems.
What is a vector field in space and how does it relate to the components P, Q, R?
-A vector field in space is a field where at every point there is a vector, and the components of this vector are functions of the coordinates x, y, and z. The components might be denoted as P, Q, R, representing the vector's direction and magnitude in relation to the coordinates.
Can you explain the concept of flux in the context of vector fields?
-Flux measures the rate at which something (like a fluid or a field) passes through a given surface. In the context of vector fields, it is the amount of the field that crosses a surface, and it is calculated using a surface integral of the dot product of the field and the unit normal vector to the surface.
What is the significance of the vector field formula given for gravitational attraction in the script?
-The formula for gravitational attraction, which is inversely proportional to the square of the distance from the origin, describes how the force field behaves around a massive object. It is an example of a vector field that is directed towards the origin and has a magnitude that decreases with distance.
How are electric fields related to vector fields discussed in the script?
-Electric fields are a type of vector field that describes the force exerted per unit charge at any point in space. In the script, they are mentioned as an example of a field that can be described using the same formula as gravitational fields, highlighting the overlap between different types of fields.
What is the difference between a line integral and a surface integral in the context of flux?
-A line integral is used to calculate flux in two-dimensional spaces, where the flow across a curve is considered. In contrast, a surface integral is used in three-dimensional spaces to measure the flux through a surface, as flow requires a two-dimensional area for it to pass through.
Can you describe the process of setting up a flux integral for a vector field through a surface?
-To set up a flux integral, one must first choose an orientation for the surface, which involves selecting a normal vector. Then, the flux integral is defined as the double integral over the surface of the dot product of the vector field and the normal vector, multiplied by the surface area element dS.
What is the significance of the normal vector in calculating flux through a surface?
-The normal vector is crucial in flux calculations because it defines the direction perpendicular to the surface. The dot product of the vector field with the normal vector gives the component of the field that is perpendicular to the surface, which is what actually contributes to the flux through the surface.
How does the script illustrate the concept of flux through a sphere with a given vector field?
-The script provides an example where the vector field is radially outward from the origin, similar to the normal vector of a sphere. By calculating the dot product of the field and the normal vector, and then integrating over the surface of the sphere, the script demonstrates how to find the total flux through the sphere.
What is the role of the divergence theorem in the context of the script?
-While not explicitly discussed in the script, the divergence theorem is hinted at as a future topic. It is a fundamental theorem in vector calculus that relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed by the surface.

Outlines

00:00

📚 Introduction to Vector Fields and Flux

This paragraph introduces the concept of vector fields in space, akin to those in the plane, with vectors at every point whose components are functions of x, y, and z. The topic of flux is presented as the next focus, with a particular emphasis on starting with flux before moving to work after Thanksgiving. Examples of vector fields include gravitational attraction and force fields, with a formula for gravitational attraction provided. The paragraph also touches on the difficulty of drawing vector fields in space and suggests that a general understanding is more practical.

05:05

🌌 Exploring Flux in Three Dimensions

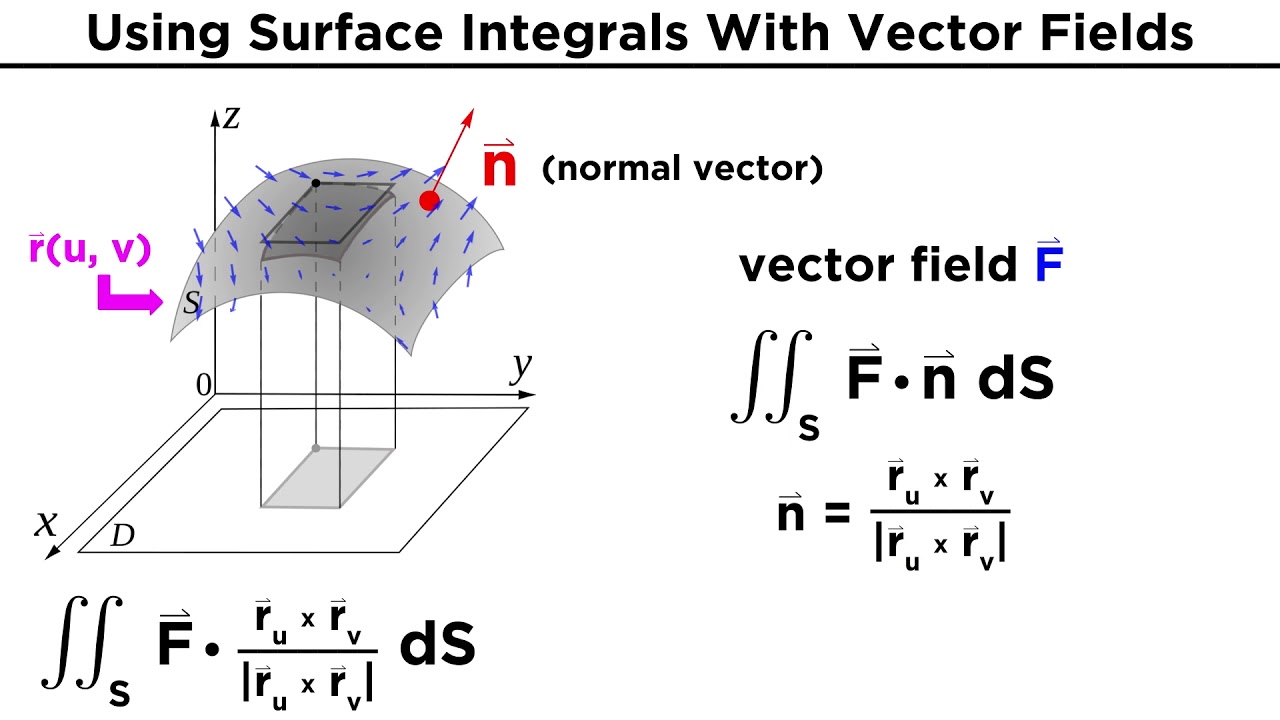
The second paragraph delves into the concept of flux in three-dimensional space, contrasting it with two-dimensional flux. It explains that flux in 3D is measured through a surface, not a line, and involves a surface integral rather than a line integral. The paragraph provides a definition of flux in 3D, involving a vector field and a surface in space, and discusses the importance of choosing an orientation for the surface to determine the direction of the normal vector, which is crucial for setting up the flux integral.

10:15

📘 Defining Flux Integral and Vector dS

This paragraph introduces the flux integral in a more formal mathematical sense, using the notation F dot n dS to represent the flux through a surface. It explains the concept of a unit normal vector and the choice of orientation for the surface. The paragraph also discusses the notation vector dS, which is a vector perpendicular to the surface with a magnitude corresponding to the surface element, and highlights its usefulness in simplifying calculations.

15:18

🌐 Calculating Flux Through a Sphere

The fourth paragraph presents an example of calculating the flux of a vector field through a sphere. It describes the vector field as radially outward from the origin and discusses the normal vector to the sphere. The example demonstrates how to set up the double integral for flux and simplifies the calculation by recognizing that the vector field and normal vector are parallel, leading to a straightforward computation of the total flux as the surface area of the sphere times the magnitude of the vector field.

20:20

📊 Flux with a Tangential Vector Field

In this paragraph, a second example is given, calculating the flux of a different vector field, this time tangent to the surface of the same sphere. The setup for the normal vector remains the same, but the vector field is now perpendicular to the radial direction. The paragraph outlines the process of calculating the dot product of the vector field and the normal vector, and then setting up the double integral over the sphere's surface to find the flux.

25:25

📈 Integrating Over Spherical Coordinates

The sixth paragraph discusses the method of integrating over the surface of a sphere using spherical coordinates, specifically phi and theta. It explains how to express the surface element dS in terms of these coordinates and how to find the bounds for the integration. The paragraph also covers the calculation of the z-component of the vector field in spherical coordinates and sets up the double integral for the flux through the sphere.

30:27

📐 Flux Through Various Surfaces

This paragraph explores the concept of flux through different types of surfaces, starting with a horizontal plane and moving on to vertical planes parallel to the yz and xz planes. It explains the normal vectors and surface elements for these planes and how to set up the double integral for flux in each case. The paragraph also touches on the use of polar coordinates and the importance of understanding the surface's orientation.

35:30

🌀 Flux Through a Cylinder and Other Surfaces

The eighth paragraph extends the discussion to flux through a cylinder and other more complex surfaces. It describes the normal vector for a cylinder and how to parameterize the surface for integration. The paragraph also mentions the process for setting up the flux integral for surfaces described by a function z = f(x, y), including the calculation of the normal vector and the surface element dS.

40:37

📘 Flux Integral Setup and Geometric Interpretation

The final paragraph provides a summary of the setup for the flux integral and its geometric interpretation. It explains the process of reducing the integral to a form that can be expressed in terms of x and y, and the importance of understanding the shadow of the surface in the x-y plane to set up bounds for integration. The paragraph concludes with a brief mention of the divergence theorem to be covered in a future class.

Mindmap

Keywords

💡Creative Commons license

The Creative Commons license is a public copyright license that allows creators to share their work while retaining certain rights. In the context of the video, it is mentioned as the license under which the content is provided, indicating that the educational material can be freely accessed and used with some restrictions, supporting the mission of MIT OpenCourseWare to offer high-quality educational resources for free.

💡MIT OpenCourseWare

MIT OpenCourseWare (OCW) is a web-based publication of virtually all MIT course content, which is available for free. The script mentions it as a platform where additional materials from hundreds of MIT courses can be viewed, highlighting the initiative's commitment to sharing knowledge and providing access to quality education globally.

💡Triple integrals

Triple integrals are a mathematical concept used to integrate functions of three variables over a three-dimensional region. The script discusses how to set up triple integrals in various coordinate systems, which is essential for understanding more complex mathematical problems in fields such as physics and engineering.

💡Vector fields

A vector field assigns a vector to every point in space, with the components of the vector depending on spatial coordinates. In the script, vector fields are introduced as the basis for understanding concepts like flux and work in three-dimensional space, with examples including gravitational and electric fields.

💡Flux

Flux, in physics, refers to the rate of transfer of a physical quantity across a surface. The script discusses flux as a concept that will be explored after Thanksgiving, indicating its importance in understanding how physical quantities, like the flow of a fluid, interact with boundaries.

💡Work

Work is a measure of energy transfer in the context of force displacing an object. Although not deeply explored in the script, it is mentioned as a topic to be covered after the discussion on flux, suggesting a connection between the effort required to move against a force field and the energy transferred.

💡Gravitational attraction

Gravitational attraction is the force by which objects with mass attract each other. In the script, it is used as an example to illustrate how a vector field can be represented, pointing towards the origin with a magnitude inversely proportional to the square of the distance from the origin.

💡Electric fields

Electric fields are vector fields that describe the force exerted per unit charge at any point in space. The script mentions electric fields as an example of a vector field, similar to gravitational fields, which can be described by the gradient of an electric potential.

💡Velocity fields

Velocity fields represent the flow of a fluid, assigning a velocity vector to each point in space. The script uses velocity fields as an example to explain how wind patterns can be modeled mathematically, with the direction and speed of the wind varying with altitude.

💡Gradient

In vector calculus, the gradient of a scalar function is a vector field that points in the direction of the greatest rate of increase of the function, with its magnitude equal to that rate. The script mentions the gradient as a method to generate a vector field from a function of three variables, such as in the case of electric or gravitational fields.

💡Surface integral

A surface integral is an integral taken over a two-dimensional surface, rather than along a curve or at a point. The script explains that flux in three-dimensional space is measured using surface integrals, which involve summing up the contributions of a vector field over all parts of a surface.

💡Unit normal vector

A unit normal vector is a vector of length one that is perpendicular (normal) to a surface at a given point. The script discusses the importance of choosing a unit normal vector to define the orientation of a surface when calculating flux, as it determines the direction in which the flux is considered to be positive.

💡Spherical coordinates

Spherical coordinates are a system of coordinates that use three values to determine a point in space: the radial distance from a fixed origin, the polar angle measured from a reference direction, and the azimuthal angle about the reference direction. The script uses spherical coordinates to simplify the calculation of flux through a sphere by allowing the surface integral to be expressed in terms of the angles phi and theta.

💡Cylindrical coordinates

Cylindrical coordinates are a three-dimensional coordinate system that specifies point positions by the distance from an origin, the angle from a reference direction, and the height above a reference plane. The script briefly mentions cylindrical coordinates as a potential system for describing the position on a cylinder when calculating flux.

💡Divergence theorem

The divergence theorem relates a surface integral of a vector field to a volume integral of the divergence of the vector field. Although not the main focus of the script, it is mentioned as a topic to be covered later, suggesting its relevance in understanding the broader principles of vector calculus and flux.

Highlights

Introduction to vector fields in space, emphasizing their importance in various physical applications such as force fields and fluid dynamics.

Explanation of vector fields as having components that are functions of coordinates x, y, and z.

Discussion on the difficulty of drawing vector fields in space and the general approach to understanding their behavior.

Introduction to the concept of flux in the context of vector fields, distinguishing it from line integrals by emphasizing its measurement through surfaces.

Definition of flux in 3D space, including the role of the unit normal vector to a surface and the choice of surface orientation.

Clarification on the difference between flux as a line integral in 2D and as a surface integral in 3D, leading to the necessity of double integrals.

Illustration of flux calculation with the example of gravitational attraction, using the formula involving the inverse square of the distance from the origin.

Introduction of the electric field as another example of a vector field, drawing parallels to the gravitational field.

Explanation of velocity fields in fluid dynamics, particularly in the context of wind patterns and their dependence on altitude.

Connection between the gradient of a function of three variables and the resulting vector field.

The overlap between different types of fields, such as electric and gravitational, and their representation through gradients.

Formal definition of the flux integral in 3D, involving the dot product of the vector field and the unit normal vector, integrated over a surface.

Introduction of the notation vector dS, representing the vector area element on a surface, and its computational advantages.

Example calculation of flux for a vector field radiating outward from the origin through a spherical surface.

Use of symmetry in the flux calculation for a vector field tangential to a sphere, leading to a simplified integral.

Transition to more complex surfaces and the general approach to setting up flux integrals for various types of surfaces.

Discussion on the use of cylindrical and spherical coordinates in setting up flux integrals for surfaces like cylinders and spheres.

Introduction of the concept of flux in relation to physical phenomena such as the amount of matter crossing a surface per unit time in a velocity field.

Preview of upcoming topics, including more detailed exploration of flux integrals, the divergence theorem, and their applications.

Transcripts

Browse More Related Video

Lec 28: Divergence theorem | MIT 18.02 Multivariable Calculus, Fall 2007

Calculus 3: Surface Integrals and Flux (Video #33) | Math with Professor V

The Divergence Theorem

Evaluating Surface Integrals

Divergence theorem proof (part 2) | Divergence theorem | Multivariable Calculus | Khan Academy

Lec 35: Final review (cont.) | MIT 18.02 Multivariable Calculus, Fall 2007

Related Tags

Vector Fields Flux Calculus MIT OCW Space Mathematics Physics Concepts Educational Resources Creative Commons Surface Integrals 3D Geometry Fluid Dynamics