Standing waves on strings | Physics | Khan Academy
TLDRThe video explains how waves behave in a medium, emphasizing the concept of standing waves, which occur when a wave reflects within a confined medium and overlaps with itself. These standing waves have specific wavelengths and frequencies, known as harmonics, which are dominant in the medium. The video uses the example of a string fixed at both ends, such as a guitar string, to illustrate how standing waves form nodes (points of no motion) and anti-nodes (points of maximum motion). It also derives a formula for calculating the wavelengths of these harmonics based on the length of the string.
Takeaways
- 🌊 Disturbing a medium can create a wave, and in an infinite medium, any wavelength or frequency is possible.
- 🏞️ In a medium with boundaries, waves reflect and overlap, creating standing waves with preferred wavelengths and frequencies.
- 🎸 A string fixed at both ends, like a guitar string, creates standing waves with nodes (points of no motion) at the ends.
- 🔄 When a wave reflects at a fixed boundary, it flips direction, and repeated pulses create overlapping waves.
- 🌀 Standing waves occur at specific wavelengths that fit within the medium, leading to a fundamental wavelength and higher harmonics.
- 🔔 The fundamental wavelength is the longest possible standing wave and dominates other wave patterns.
- 🔄 In standing waves, nodes (no motion) and antinodes (maximum motion) form due to constructive and destructive interference.
- 📏 The wavelength of standing waves can be calculated using the formula: 2L/n, where L is the string length and n is the harmonic number.
- 🔄 Harmonics are labeled by the number of nodes, with the fundamental having no nodes in the middle, the second harmonic having one, and so on.
- 🎼 Standing waves are crucial in understanding the physics of musical instruments, determining the notes they produce.
Q & A
What happens when a wave is created in a medium with no boundaries?
-In a medium with no boundaries, the wave can propagate indefinitely without reflecting, allowing for any wavelength or frequency to be created.
What is a standing wave?
-A standing wave is formed when a wave reflects off boundaries and overlaps with itself, creating points of no motion (nodes) and points of maximum motion (anti-nodes).
Why are standing waves important to study?
-Standing waves are important because they select preferred wavelengths and frequencies, which often become dominant. This is crucial in understanding resonance in various systems, such as musical instruments.
What is a node in the context of waves?
-A node is a point along a standing wave where there is no motion, caused by destructive interference between the wave traveling in one direction and its reflection.
How does a string fixed at both ends, like a guitar string, relate to standing waves?
-A string fixed at both ends, such as a guitar string, can support standing waves. The physics of standing waves determine the possible notes the string can produce based on its length and tension.
What is the fundamental wavelength of a standing wave on a string?
-The fundamental wavelength is the longest possible wavelength that fits on the string with nodes at both ends. It is often the dominant wavelength and is also called the first harmonic.
How does the reflection of a wave on a string affect its phase?
-When a wave reflects off a fixed boundary (a node), it inverts its phase, meaning the reflected wave is flipped upside down compared to the incoming wave.
How do you determine the possible wavelengths that can form standing waves on a string?
-Possible wavelengths for standing waves can be found by drawing the wave and ensuring there are nodes at each end of the string. Mathematically, the nth harmonic wavelength is given by λ = 2L/n, where L is the length of the string and n is the harmonic number.
What is the relationship between harmonics and nodes on a string?
-The fundamental wave (first harmonic) has no nodes in the middle, the second harmonic has one node in the middle, the third harmonic has two nodes, and so on. Each higher harmonic introduces an additional node.
How does the length of the string affect the wavelength of standing waves?
-The length of the string determines the wavelengths of the standing waves that can form. For example, the fundamental wavelength is twice the length of the string, and each subsequent harmonic's wavelength is a fraction of this length (e.g., L, 2L/3, L/2, etc.).
What is the pattern for determining the wavelength of the nth harmonic?
-The wavelength of the nth harmonic on a string fixed at both ends can be calculated using the formula λ = 2L/n, where L is the length of the string and n is the harmonic number.
Outlines
🌊 Understanding Waves in Unbounded and Bounded Mediums
In this section, the instructor introduces the concept of waves in mediums with and without boundaries. Waves in a medium without boundaries can have any wavelength or frequency, while waves in a bounded medium reflect and overlap, creating standing waves. These standing waves have preferred wavelengths and frequencies, which are crucial for studying wave behavior. The example of a string fixed at both ends, like guitar or piano strings, is used to illustrate how standing waves are formed and how nodes (points with no motion) and antinodes (points of maximum motion) are established.
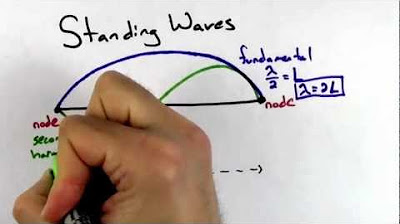
🎸 Fundamental and Harmonic Standing Waves on Strings
This section explains how standing waves can be visualized on a string fixed at both ends. The instructor describes the fundamental wavelength, the largest possible standing wave, which appears like a jump rope with nodes at both ends. The fundamental wavelength is dominant among all possible wavelengths. The next possible standing wave is the second harmonic, followed by the third harmonic, and so on. These harmonics have additional nodes in the middle. The concept of constructive and destructive interference is introduced to explain the formation of nodes and antinodes in standing waves.
📏 Calculating Wavelengths of Harmonics
In this section, the instructor discusses how to calculate the wavelengths of different harmonics on a string of a given length. By considering the length of the string (10 meters in this example), the wavelengths of the fundamental and higher harmonics are determined. The first harmonic (fundamental wavelength) is half the length of the string, the second harmonic equals the string length, the third harmonic is two-thirds the string length, and so on. A general formula for the wavelength of the nth harmonic is provided: \( \lambda_n = \frac{2L}{n} \), where L is the length of the string and n is the harmonic number. This formula is crucial for calculating the wavelengths without drawing the wave patterns for each harmonic.
Mindmap
Keywords
💡Wave
💡Medium
💡Boundary
💡Standing Wave
💡Node
💡Anti-node
💡Harmonic
💡Fundamental Wave
💡Wavelength
💡Frequency
Highlights
Creating a wave in a medium without boundaries allows waves of any wavelength or frequency.
Confined waves in a medium with boundaries reflect and overlap, forming standing waves.
Standing waves select preferred wavelengths and frequencies, making them important to study.
Nodes are points on a wave with no motion, while anti-nodes are points of maximum displacement.
The fundamental wavelength is the longest and most dominant standing wave on a string.
The first harmonic wave resembles a simple jump rope motion.
The second harmonic wave introduces one node in the middle of the string.
The third harmonic wave has two nodes in the middle of the string.
As the harmonic number increases, the number of nodes in the middle of the string also increases.
Nodes occur due to destructive interference, while anti-nodes result from constructive interference.
Wave reflections at fixed boundaries result in wave direction flipping.
The formula for the wavelength of the nth harmonic is 2L/n, where L is the string length.
This formula applies to strings with nodes at both ends, common in musical instruments.
Standing waves oscillate up and down rather than left to right, appearing to 'stand still'.
Instruments like guitars and pianos use the physics of standing waves to produce sound.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: