Surface integral ex3 part 3: Top surface | Multivariable Calculus | Khan Academy
TLDRIn this instructional video, the instructor guides through the process of evaluating a surface integral over the top part of a modified cylinder. The focus is on parameterizing the surface using polar coordinates, with x and y taking values within the unit circle and z being a function of x. The parameterization involves varying both the angle (theta) and the radius (r), resulting in a position vector function for the surface. The script also covers the calculation of the cross product and the magnitude of the normal vector for the surface integral, setting up for the actual integration in a subsequent video.
Takeaways
- 📚 The lesson is focused on evaluating a surface integral over a specific part of a geometric shape, which is the top part of a 'chopped cylinder'.
- 📐 The shape is parameterized using polar coordinates, considering the x and y values as functions of a radius (r) and an angle (theta), within the unit circle.
- 🔍 The z-value is determined by the function z = 1 - x, where x is a function of r and theta (x = r * cos(theta)).
- 📈 The parameterization involves varying both the angle (theta) from 0 to 2π and the radius (r) from 0 to 1 to cover all points on the surface.
- 📝 A position vector function is introduced to represent points on the surface, denoted as 'surface three' and parameterized by r and theta.
- 🤔 The cross product of the partial derivatives with respect to r and theta is calculated to find the normal vector for the surface integral.
- 🧩 The cross product simplifies to a magnitude of the normal vector that is the square root of two times r, indicating a dependency on the radius.
- 📉 The integral involves the z component (1 - r * cos(theta)) and the magnitude of the normal vector, with the integral to be evaluated over r and theta.
- 🔢 The setup for the integral includes the boundaries for r (0 to 1) and theta (0 to 2π), with the integral ready to be evaluated in the subsequent lesson.
- 👨🏫 The instructor plans to continue the evaluation of the integral in a follow-up video, indicating that the current script ends with the setup for integration.
- 📚 The script is part of a series of lessons, likely focused on multivariable calculus, given the context of surface integrals and parameterization.
Q & A
What is the topic of the video script?
-The topic of the video script is the evaluation of a surface integral over a specific part of a geometric shape, which is described as a chopped cylinder.
What is the 'home stretch' mentioned in the script referring to?
-The 'home stretch' is a colloquial term used to refer to the final part of a task or process, indicating that the instructor is nearing the completion of the surface integral evaluation.
What type of integral is being evaluated in the script?
-The script is focused on evaluating a surface integral, specifically over the top part of a chopped cylinder.
Why is polar coordinate system considered for parameterization in the script?
-The polar coordinate system is considered for parameterization because it simplifies the representation of points within and on the boundary of the unit circle, which is the region of integration.
What is the significance of the unit circle in this context?
-The unit circle is significant as it defines the region in the xy-plane where the x and y values for the surface integral can vary, including the boundary of the circle.
How is the top surface of the chopped cylinder described in terms of z?
-The top surface of the chopped cylinder is described as a subset of the plane where z is equal to one minus x, intersecting with the unit circle in the xy-plane.
What parameters are chosen for the parameterization of the surface?
-The parameters chosen for the parameterization are r (radius) and theta (angle), which vary over the unit circle and from 0 to 1 for r, and from 0 to 2π for theta.
What is the parameterization of the surface in terms of the position vector function?
-The parameterization of the surface is given by the position vector function that depends on r and theta, resulting in x = r*cos(theta), y = r*sin(theta), and z = 1 - r*cos(theta).
What is the purpose of calculating the cross product of the partial derivatives in the script?
-The cross product of the partial derivatives is calculated to find the normal vector to the surface, which is necessary for evaluating the surface integral.
How does the magnitude of the cross product simplify in the script?
-The magnitude of the cross product simplifies to the square root of two times r, which is a significant simplification that helps in evaluating the surface integral.
What is the next step after setting up the integral as described in the script?
-The next step, as mentioned in the script, is to set up the boundaries of integration and then evaluate the integral, which will be continued in the next video.
Outlines
📚 Evaluating the Surface Integral Over a Chopped Cylinder
In this segment, the instructor discusses the process of evaluating a surface integral over the top part of a modified cylinder. The focus is on parameterizing the surface using polar coordinates with x and y values constrained within the unit circle and z values determined by a function of x. The parameterization involves two parameters, r (radius) and theta (angle), with r ranging from 0 to 1 and theta from 0 to 2π. The position vector function is introduced to represent points on the surface, and the z value is expressed as a function of x, which in turn is a function of r and theta. The instructor prepares to set up the integral but does not complete it within this paragraph.
🔍 Calculating the Cross Product for Surface Integral Evaluation
The instructor continues by explaining the next steps in evaluating the surface integral, which involves calculating the cross product of the partial derivatives of the position vector function with respect to r and theta. The partial derivatives are computed, and the cross product is simplified to a form involving r and the squared trigonometric functions of theta. The magnitude of the cross product is derived, leading to the expression for the differential surface element dS. The instructor sets up the integral involving the z component and the differential surface element but does not proceed to evaluate the integral within this paragraph.
📝 Setting Up the Integration for the Surface Integral
In the final paragraph, the setup for the actual integration process is detailed. The instructor expresses the surface integral in terms of the z component, which is a function of r and theta, and the differential surface element dS, which includes the magnitude of the cross product derived earlier. The integral is set up with respect to both r and theta, with the intention to evaluate it in the subsequent video. The instructor acknowledges the time constraint and decides to continue the evaluation in the next video, leaving the integration boundaries and the final evaluation for future discussion.
Mindmap
Keywords
💡Surface Integral
💡Parameterization
💡Polar Coordinates
💡Unit Circle
💡Cross Product
💡Partial Derivative
💡Normal Vector
💡Magnitude
💡Integration Boundaries
💡Differential Surface Area Element (dS)
Highlights
Evaluating the third surface integral over the top part of a chopped cylinder.
Parameterization of the surface using polar coordinates for easier calculation.
The top surface S3 is a subset of the plane z = 1 - x, intersecting the unit circle.
Using theta as the parameter for the angle around the unit circle.
Introducing a variable radius r to account for all xy values inside and outside the unit circle.
Parameter ranges for r (0 to 1) and theta (0 to 2π) to cover the entire unit circle.
Parameterization of x, y, and z in terms of r and theta.
Expression for z as a function of x, specifically z = 1 - x.
Formulation of the position vector function for surface S3.
Cross product of partial derivatives with respect to r and theta to find the normal vector.
Simplification of the cross product components to isolate i and k components.
Observation that the j component of the cross product is zero due to cancellation.
Magnitude of the cross product simplifies to √2r.
Expression for ds, the differential surface element, in terms of r, theta, and the cross product magnitude.
Setting up the surface integral of z ds over the parameterized surface S3.
Integration of the function z = 1 - r cos(theta) with respect to r and theta.
Factoring out constants like √2 to simplify the integral expression.
Continuation of the integral evaluation in the next video due to time constraints.
Transcripts
Browse More Related Video

Stokes example part 2: Parameterizing the surface | Multivariable Calculus | Khan Academy

Divergence theorem proof (part 3) | Divergence theorem | Multivariable Calculus | Khan Academy

Stokes' theorem proof part 2 | Multivariable Calculus | Khan Academy
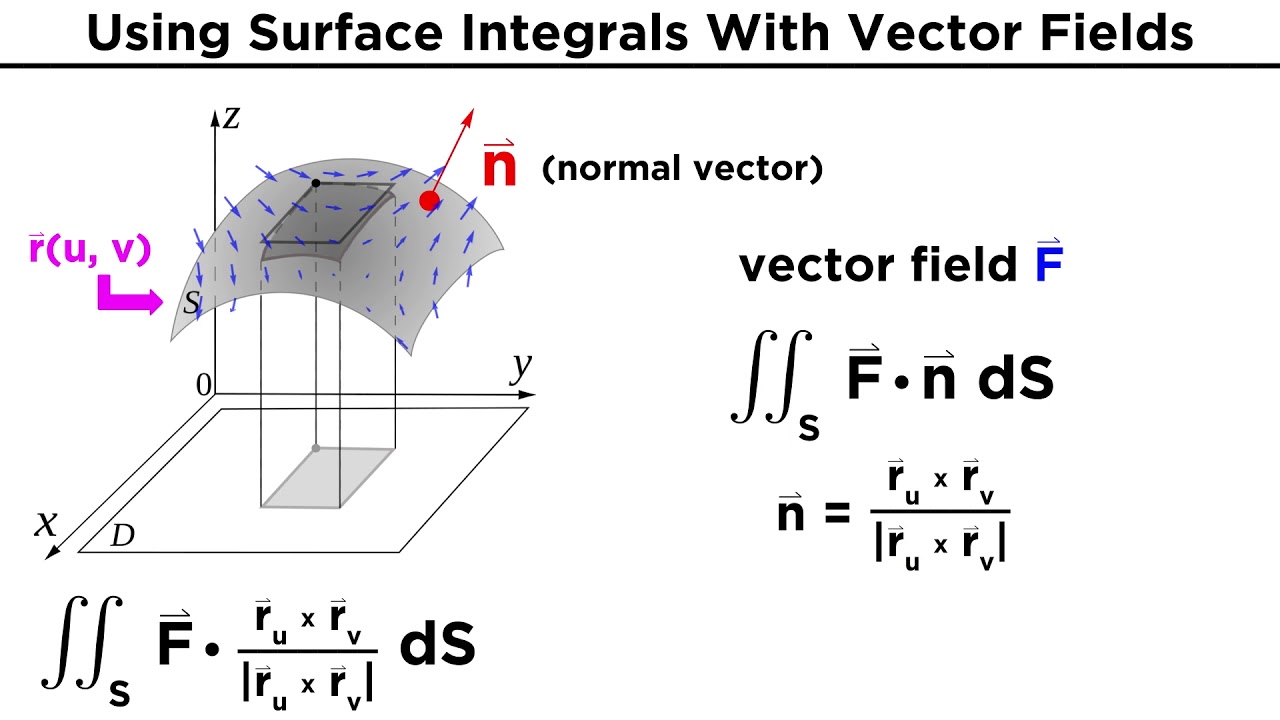
Evaluating Surface Integrals

Calculus 3: Surface Integrals and Flux (Video #33) | Math with Professor V

Introduction to parametrizing a surface with two parameters | Multivariable Calculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: