Vector representation of a surface integral | Multivariable Calculus | Khan Academy
TLDRThis educational video script explores the concept of surface integrals and simplifies their calculation by introducing the unit normal vector to a surface. It explains how to substitute the unit normal vector into the integral formula, leading to a simplification that involves a double integral over the uv domain. The script also delves into alternative representations of surface integrals, providing intuitive understanding through the use of differentials and cross products, ultimately showing how these integrals can be expressed as a dot product with a vector differential, ds.
Takeaways
- 📚 The video discusses the process of constructing a unit normal vector to a surface and its application in simplifying surface integrals.
- 🔍 It explains how substituting the unit normal vector into the surface integral formula can lead to simplifications.
- 📐 The script introduces the concept of ds, which represents an infinitesimal area element on the surface, and its relation to the cross product of partial derivatives.
- 🧩 The video demonstrates that the magnitude of the cross product in the integral's denominator and numerator can cancel each other out, simplifying the integral.
- 📉 By rewriting the integral in terms of the uv domain, the surface integral transforms into a double integral, making calculations more manageable.
- 📝 The script clarifies that the double integral over the uv plane corresponds to a region in the parameter space, not the actual surface.
- 🔄 The video shows an alternative representation of the surface integral by rewriting the differential area element as a vector, emphasizing its geometric interpretation.
- 📈 It introduces the notation ds with a vector to represent the differential area element as a vector normal to the surface, which is crucial for understanding surface integrals.
- 📖 The script explains that the surface integral can be rewritten using the vector differential ds, which simplifies the calculation process.
- 🔑 The video highlights three different ways to represent the surface integral, emphasizing the flexibility in mathematical notation based on the context.
- 🎯 The final takeaway is that understanding the geometric interpretation of the integral components is essential for effectively calculating surface integrals.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the construction of a unit normal vector to a surface and its application in simplifying the calculation of surface integrals.
What is the significance of the unit normal vector in surface integrals?
-The unit normal vector is significant in surface integrals as it helps in simplifying the integral by providing a direction that is perpendicular to the surface, which is essential for calculating the flux or other surface integral properties.
How does the script simplify the expression for the surface integral of a vector field F?
-The script simplifies the expression by showing that the division and multiplication by the magnitude of the cross product of the partial derivatives essentially cancel each other out, leading to a double integral over the uv plane of the vector field F dotted with the cross product of the partial derivatives.
What does 'ds' represent in the context of the script?
-'ds' in the script represents an infinitesimal element of the surface area, which can be thought of as a small chunk of area in the uv plane or the uv domain.
What is the difference between a scalar 'ds' and the vector 'ds' mentioned in the script?
-The scalar 'ds' represents the infinitesimal area element on the surface, while the vector 'ds' is a differential that includes direction, pointing normally from the surface with a magnitude equal to the area defined by the two vectors from the partial derivatives.
Why is the cross product of the partial derivatives with respect to u and v important in the script?
-The cross product of the partial derivatives with respect to u and v is important because it gives a vector that is orthogonal to the surface, which is essential for defining the unit normal vector and calculating the surface integral.
How does the script suggest rewriting the surface integral in terms of the vector differential 'ds'?
-The script suggests rewriting the surface integral by replacing the scalar area element 'ds' with the vector differential 'ds', which includes both direction and magnitude, simplifying the expression to the integral of the vector field F dotted with 'ds'.
What is the purpose of the parameterization in the context of the script?
-The purpose of parameterization in the script is to express the surface integral in terms of a double integral over the uv domain, which simplifies the process of calculating the integral by converting it into a more manageable form.
How does the script explain the intuition behind the vector differential 'ds'?
-The script explains the intuition behind the vector differential 'ds' by conceptualizing it as a small change along the surface in the u and v directions, and taking the cross product of these changes to obtain a vector normal to the surface with a magnitude equal to the area defined by these changes.
What is the significance of the magnitude of the cross product in the script?
-The magnitude of the cross product is significant as it represents the area spanned by the two vectors resulting from the partial derivatives, which is crucial for understanding the surface area element 'ds' in the context of surface integrals.
How does the script connect the concept of surface integrals to the idea of a unit normal vector?
-The script connects the concept of surface integrals to the idea of a unit normal vector by showing that the vector differential 'ds' can be thought of as a unit normal vector times the scalar area element, thus simplifying the expression for the surface integral.
Outlines
📚 Introduction to Simplifying Surface Integrals
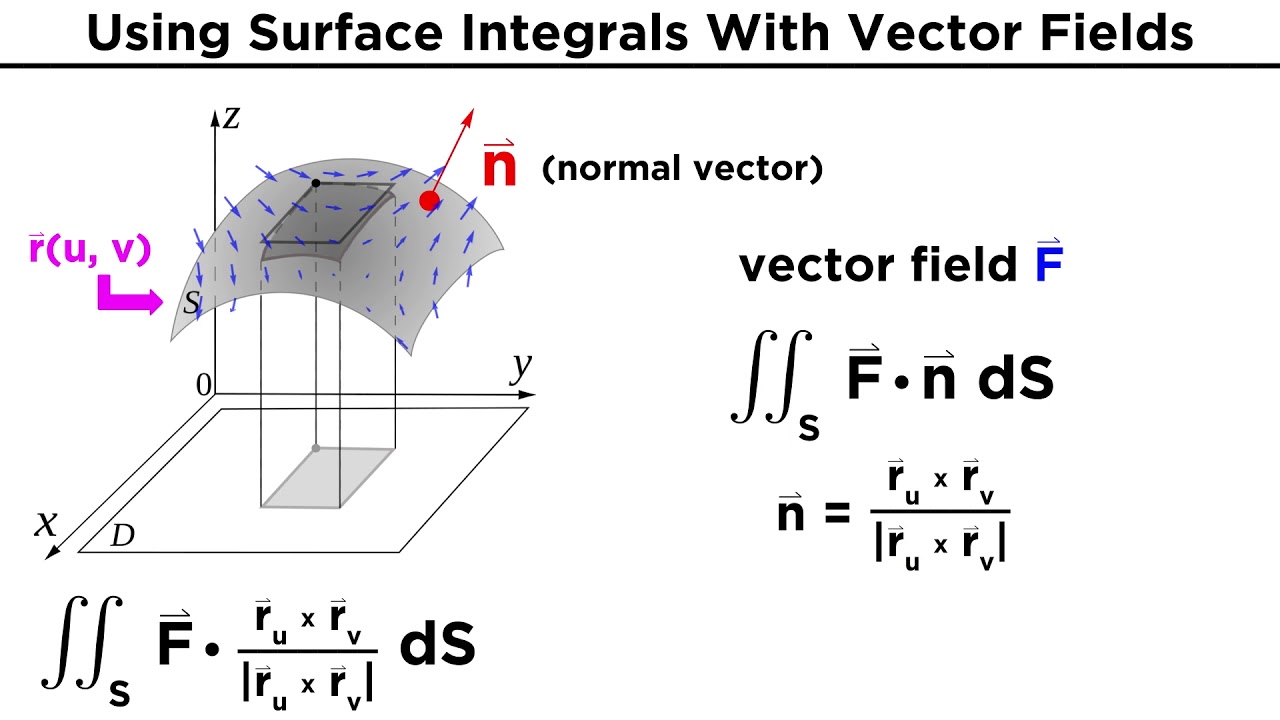
The script begins by revisiting the construction of a unit normal vector to a surface, a concept previously covered. The aim is to apply this knowledge to simplify the original surface integral calculation. The script introduces the notation for the surface integral of a vector field F, emphasizing the role of the unit normal vector in the calculation. It also discusses alternative representations of surface integrals and hints at a simplification involving the magnitude of the cross product of partial derivatives of a parameterized surface, ultimately suggesting that these operations cancel each other out, simplifying the integral.
🔍 Deep Dive into Surface Integral Calculations
This paragraph delves deeper into the calculation of surface integrals, focusing on the parameterization of surfaces and the transformation of a surface integral into a double integral over the uv domain. The script explains how the differential area element ds can be represented in terms of the cross product of partial derivatives and how this leads to a simplification in the integral. It also introduces the concept of rewriting the integral using a vector differential ds, which represents an infinitesimal change on the surface, leading to a more intuitive understanding of the surface integral as a product of the vector field and this vector differential.
Mindmap
Keywords
💡Unit Normal Vector
💡Surface Integral
💡Partial Derivative
💡Cross Product
💡Magnitude
💡Parameterization
💡UV Domain
💡Differential Area
💡Dot Product
💡Vector Field
💡Double Integral
Highlights
Introduction to constructing a unit normal vector to a surface and its application in simplifying surface integrals.
Substitution of the unit normal vector into the original surface integral formula.
Explanation of the surface integral of F dot with the cross product of partial derivatives.
Understanding ds as the magnitude of the cross product of partial derivatives of r with respect to u and v.
Transition from surface integral to a double integral over the uv domain.
Simplification of the integral by canceling out the magnitude of the cross product.
The integral simplifies to a double integral over the region in the uv plane.
Parameterization allows expressing everything in terms of a double integral in the uv domain.
Exploration of alternative representations of surface integrals for better intuition.
Rewriting the cross product of partial derivatives with scalar du and dv.
Conceptualization of the differential of r in the u-direction as a vector.
Cross product of differentials of r in u and v directions gives a normal vector to the surface.
The magnitude of the cross product vector is equal to the area defined by the two differentials.
Rewriting the surface integral using the vector differential ds.
Differentiating between the scalar ds and the vector differential ds in the context of surface integrals.
Common usage of the vector differential ds in calculating surface integrals.
Transcripts
Browse More Related Video
Evaluating Surface Integrals

Divergence theorem proof (part 2) | Divergence theorem | Multivariable Calculus | Khan Academy

Divergence theorem proof (part 3) | Divergence theorem | Multivariable Calculus | Khan Academy

Calculus 3: Surface Integrals and Flux (Video #33) | Math with Professor V

Stokes example part 3: Surface to double integral | Multivariable Calculus | Khan Academy

Constructing a unit normal vector to a surface | Multivariable Calculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: