Math 14 7.1.13 Find the point estimate, margin of error & confidence interval of pop. proportion p.

Fiorentino Siciliano
31 Mar 202309:52
EducationalLearning
32 Likes 10 Comments

TLDRThe video transcript details a statistical analysis on the vulnerability to identity theft, using a sample size of 920 with 536 respondents affirming their concern. It explains calculating the point estimate of the population proportion (0.583), determining the margin of error (0.032) at a 95% confidence level, and constructing the resulting confidence interval (0.551 to 0.615). The script concludes with the interpretation of the confidence interval, indicating 95% certainty that the true population proportion lies within the interval.

Takeaways
  • πŸ” The research institute conducted a poll with a sample size of 920 respondents to gauge feelings of vulnerability to identity theft.
  • πŸ“Š Of the 920 respondents, 536 indicated they felt vulnerable, which is used as the sample statistic for further analysis.
  • 🎯 The point estimate of the population proportion (p) is calculated as the number of 'yes' responses (536) divided by the total sample size (920), resulting in 0.583.
  • πŸ“ The margin of error (E) is determined using the formula involving the critical value of Z, the point estimate, and the sample size, yielding a result of 0.032.
  • πŸ“š The critical value of Z for a 95% confidence level and an area to the right of 0.025 is found to be 1.96 using statistical software.
  • πŸ“‰ The complement of the point estimate (1 - pΜ‚) is calculated to be 0.417, which is necessary for the margin of error formula.
  • πŸ“Œ The confidence interval is constructed by adding and subtracting the margin of error from the point estimate, resulting in a range from 0.551 to 0.615.
  • βœ… The constructed confidence interval meets the requirements for estimating a population proportion, including having at least five successes and failures.
  • πŸ—£οΈ The correct interpretation of the confidence interval is that there is a 95% confidence that the true population proportion of feeling vulnerable to identity theft lies between 0.551 and 0.615.
  • πŸ“‹ The script provides a step-by-step guide on calculating the point estimate, margin of error, and constructing a confidence interval for a population proportion.
Q & A

  • What is the sample size (n) in the research institute poll regarding vulnerability to identity theft?

    -The sample size (n) in the poll is 920.

  • How many respondents in the poll said 'yes' to feeling vulnerable to identity theft?

    -536 respondents in the poll said 'yes' to feeling vulnerable to identity theft.

  • What is the best point estimate of the population proportion (p) based on the poll results?

    -The best point estimate of the population proportion is 0.583, which is calculated by dividing the number of 'yes' respondents (536) by the sample size (920).

  • What is the significance of rounding the point estimate to three decimal places?

    -Rounding to three decimal places provides a precise yet manageable level of accuracy for the point estimate, making it easier to interpret and use in further calculations.

  • What is the formula used to calculate the margin of error (E) in this context?

    -The margin of error is calculated using the formula E = Z * sqrt[(pΜ‚ * (1 - pΜ‚)) / n], where Z is the critical value from the Z-distribution corresponding to the desired confidence level, pΜ‚ is the point estimate, and n is the sample size.

  • What is the critical value of Z for a 95% confidence level?

    -The critical value of Z for a 95% confidence level is 1.96, which corresponds to the area to the right of 0.025 in a standard normal distribution.

  • How is the complement of the point estimate used in the margin of error formula?

    -The complement of the point estimate (1 - pΜ‚) is used in the margin of error formula to account for the variability in the sample proportion, ensuring that both the point estimate and its uncertainty are considered.

  • What is the calculated margin of error for the poll results?

    -The calculated margin of error for the poll results is 0.032, which is derived from the formula and rounded to three decimal places for clarity.

  • How is the confidence interval constructed based on the point estimate and margin of error?

    -The confidence interval is constructed by taking the point estimate and subtracting and adding the margin of error to it, resulting in a range that likely contains the true population proportion.

  • What is the confidence interval for the poll results regarding vulnerability to identity theft?

    -The confidence interval for the poll results is from 0.551 to 0.615, indicating that with 95% confidence, the true population proportion of people feeling vulnerable to identity theft lies within this range.

  • How should the confidence interval be interpreted in the context of the poll?

    -The confidence interval should be interpreted as providing a range within which we are 95% confident that the true population proportion of people feeling vulnerable to identity theft falls.

Outlines
00:00
πŸ” Calculating Point Estimate and Margin of Error

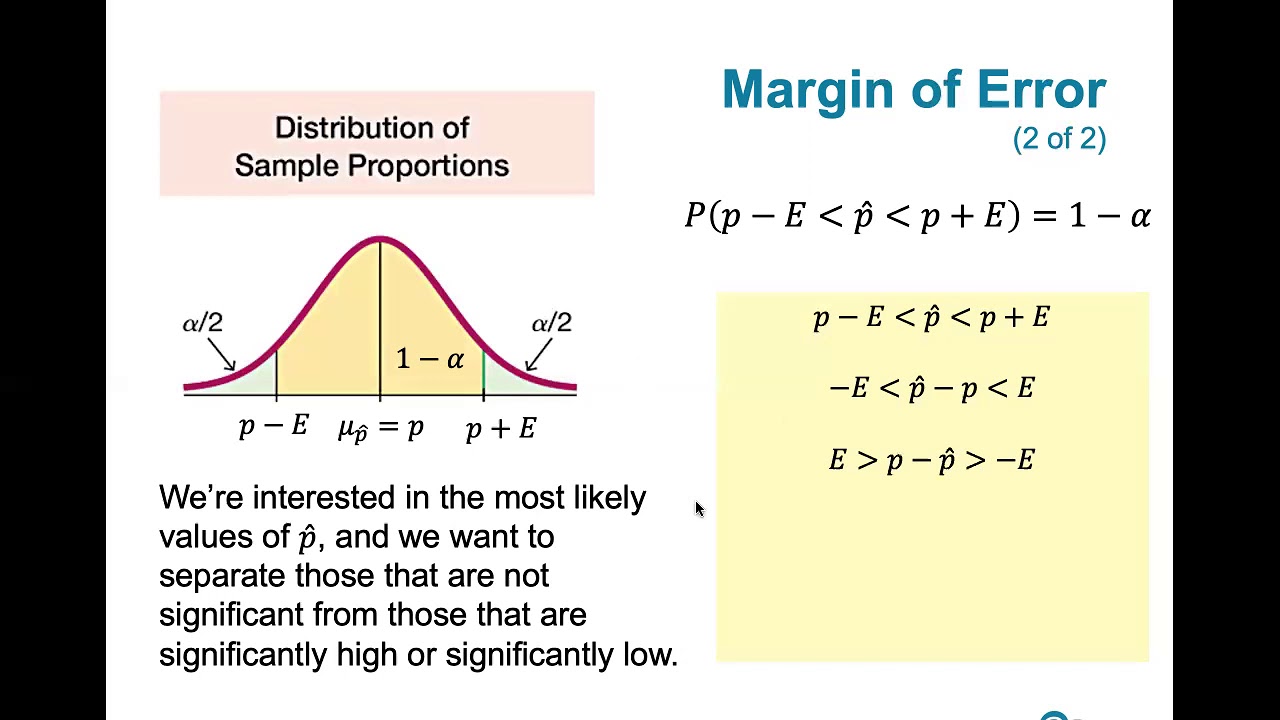
This paragraph explains the process of determining the point estimate for the population proportion 'p' using a sample size (n=920) and the number of affirmative responses (X=536) to a poll about vulnerability to identity theft. The point estimate is calculated as X/n and rounded to three decimal places, resulting in 0.583. Subsequently, the margin of error 'E' is found using the formula involving the critical value of Z, the square root of the point estimate, and its complement, all divided by the sample size. With a 95% confidence level, Alpha is calculated as 0.05, and the critical Z-value is determined to be 1.96 using a statistical tool. The margin of error is then computed and rounded to three decimal places, yielding 0.032.

05:02
πŸ“Š Constructing and Interpreting Confidence Interval

The second paragraph focuses on the construction of a confidence interval for the population proportion, ensuring that the conditions for a binomial distribution are met, such as having at least five successes and failures. Using the previously calculated point estimate (0.583) and margin of error (0.032), the confidence interval is established by subtracting and adding the margin of error to the point estimate, resulting in a range from 0.551 to 0.615. The paragraph concludes with an interpretation of the confidence interval, stating that there is a 95% confidence that the true population proportion lies within this interval, and correctly identifies the answer choice as B.

Mindmap
Keywords
πŸ’‘Point Estimate
A point estimate is a single value that serves as the best guess for an unknown parameter based on a sample. In the video, the point estimate for the population proportion is calculated by dividing the number of 'yes' responses (536) by the total sample size (920), resulting in 0.583. This estimate is crucial as it provides a single value that represents the central tendency of the data regarding the respondents' vulnerability to identity theft.
πŸ’‘Confidence Level
The confidence level is the probability that an interval estimate encompasses the true population parameter. In the script, a 95 percent confidence level is used, indicating that if the poll were repeated many times, the interval would capture the true population proportion in 95 out of 100 instances. This concept is central to understanding the reliability of the poll's results.
πŸ’‘Margin of Error
The margin of error represents the range within which the true population parameter is likely to fall, given the sample data and confidence level. In the video, the margin of error is calculated using the formula involving the critical value of Z, the point estimate, and the sample size. The calculated margin of error is 0.032, which is used to construct the confidence interval and reflects the precision of the estimate.
πŸ’‘Critical Value of Z
The critical value of Z is a value from the standard normal distribution that corresponds to the desired confidence level. In the context of the video, the critical value of Z is found to be 1.96, which corresponds to the 95 percent confidence level. This value is used in the formula to calculate the margin of error, indicating the number of standard deviations from the mean that define the confidence interval.
πŸ’‘Complement of the Point Estimate
The complement of the point estimate is calculated by subtracting the point estimate from 1. In the script, the point estimate is 0.583, so its complement is 0.417. This concept is used in the margin of error formula to account for the variability in the data, as it represents the proportion of respondents who said 'no' to the poll's question.
πŸ’‘Confidence Interval
A confidence interval is a range of values, derived from a sample, that is likely to contain the true population parameter. The video explains how to construct a 95 percent confidence interval for the population proportion using the point estimate and the margin of error. The resulting interval is from 0.551 to 0.615, providing a range within which the true proportion of respondents feeling vulnerable to identity theft is likely to fall.
πŸ’‘Sample Size
The sample size refers to the number of observations or elements in the sample. In the video, the sample size is 920, which is the total number of respondents to the poll. The sample size is important as it affects the precision of the point estimate and the width of the confidence interval.
πŸ’‘Binomial Distribution
The binomial distribution is a probability distribution that describes the number of successes in a fixed number of independent Bernoulli trials with the same probability of success. In the context of the video, the conditions for the binomial distribution are assumed to be met, which is a requirement for using the formula to calculate the margin of error.
πŸ’‘Successes and Failures
In the context of the poll, 'successes' refer to the number of respondents who answered 'yes' to feeling vulnerable to identity theft, which is 536. 'Failures' would be the remaining respondents who answered 'no'. The video mentions that there are at least five successes and failures, which is a condition for constructing a valid confidence interval using the binomial distribution.
πŸ’‘StatCrunch
StatCrunch is a statistical software mentioned in the video used for calculating probabilities and critical values from statistical distributions. In this case, it is used to find the critical value of Z corresponding to the 95 percent confidence level, which is essential for determining the margin of error.
Highlights

A research institute conducted a poll on vulnerability to identity theft with a sample size of 920 respondents.

536 respondents indicated they felt vulnerable to identity theft, representing the sample's 'yes' responses.

The best point estimate of the population proportion (p) was calculated to be 0.583.

The calculation of the point estimate involved dividing the number of 'yes' responses by the sample size and rounding to three decimal places.

A 95% confidence level was chosen for the analysis.

The margin of error (E) was determined using the formula involving the critical value of Z, point estimate, and sample size.

The critical value of Z for a 95% confidence level and an area to the right of 0.025 was found to be 1.96 using StatCrunch.

The margin of error was calculated to be 0.032, rounded to three decimal places.

The confidence interval construction requirements were checked, confirming the sample was a simple random sample with sufficient successes and failures.

The lower limit of the confidence interval was calculated as 0.551.

The upper limit of the confidence interval was determined to be 0.615.

The confidence interval indicates that there is a 95% confidence that the true population proportion lies between 0.551 and 0.615.

The interpretation of the confidence interval was correctly stated, indicating the range within which the true population proportion is likely to fall.

The correct answer for the interpretation of the confidence interval was identified as option B.

The process of determining the margin of error and confidence interval followed standard statistical methods for estimating population proportions.

The use of StatCrunch software facilitated the finding of the critical Z value for the given confidence level.

The importance of checking the conditions for constructing a confidence interval was emphasized to ensure the validity of the results.

Transcripts

Browse More Related Video

How to construct a confidence interval for the proportion, an example

Confidence Interval for a population proportion | Solved Problems

Math 14 HW 7.2.5-T Find critical t value, margin of error & confidence interval for population mean.

Finding the best point estimate and confidence interval for proportions

7.1.4 Estimating a Population Proportion - Margin of Error and Computing Confidence Intervals

Confidence interval example | Inferential statistics | Probability and Statistics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Confidence IntervalPopulation ProportionStatistical AnalysisMargin of ErrorSample SizeResearch PollIdentity TheftCritical ValueZ-ScoreEstimation