Math 14 HW 7.2.5-T Find critical t value, margin of error & confidence interval for population mean.

Fiorentino Siciliano

5 Apr 202308:57

EducationalLearning

32 Likes 10 Comments

TLDRThis video script provides a detailed walkthrough of calculating a 95% confidence interval for the mean weight of newborn girls based on a sample of 36. It explains determining the critical T value using a T-distribution, calculating the margin of error, and ensuring the sample meets the criteria for constructing a confidence interval. The script concludes with the formula for the confidence interval and an interpretation of its meaning, emphasizing the 95% confidence that the interval contains the true population mean weight.

Takeaways

📊 The script discusses a statistical analysis involving the weights of newborn girls, with a sample size of 36.
🔢 The sample mean weight is reported as 3216.7 grams, with a standard deviation of 688.5 grams.
📉 A 95% confidence level is used to determine the critical T value for the margin of error.
📍 The critical T value is calculated to be 2.03 using a T-distribution with 35 degrees of freedom.
🧐 The margin of error is derived using the formula: critical T value * sample standard deviation / √n, resulting in 232.9 grams.
📐 The script verifies that the requirements for constructing a confidence interval are met, as the sample size is greater than 30.
📈 The confidence interval for the population mean is calculated to be between 2983.8 grams and 3449.6 grams.
📝 The script emphasizes the importance of understanding the confidence interval as a range that likely contains the true population mean.
🤔 It is noted that the confidence level represents the success rate of the procedure used to construct the confidence interval.
📚 The script provides a step-by-step guide on how to calculate the critical T value, margin of error, and confidence interval.
🔍 The use of StatCrunch software is mentioned for finding the critical T value and completing the statistical analysis.

Q & A

What is the sample size (n) for the weights of newborn girls in the study?
-The sample size is 36.
What is the sample mean weight (X bar) of the newborn girls?
-The sample mean weight is 3216.7 grams.
What is the sample standard deviation for the weights of the newborn girls?
-The sample standard deviation is 688.5 grams.
What confidence level is used in the study?
-A 95% confidence level is used.
How is the critical T value determined for the margin of error?
-The critical T value is found using the degrees of freedom, which is the sample size minus one (35 in this case), and the area in the right tail of the T distribution corresponding to the confidence level (0.025 for 95% confidence).
What is the critical T value obtained from the T distribution table?
-The critical T value is 2.03.
How is the margin of error calculated in this study?
-The margin of error is calculated as the critical T value (2.03) times the sample standard deviation (688.5) divided by the square root of the sample size (6).
What is the calculated margin of error for the weights of the newborn girls?
-The margin of error is 232.9 grams.
What are the requirements for constructing a confidence interval to estimate a population mean?
-The requirements are that the sample is a simple random sample and either the population is normally distributed or the sample size is greater than 30.
What is the lower limit of the 95% confidence interval for the mean weight of newborn girls?
-The lower limit is 2983.8 grams.
What is the upper limit of the 95% confidence interval for the mean weight of newborn girls?
-The upper limit is 3449.6 grams.
How should the confidence interval be interpreted?
-The confidence interval can be interpreted as having a 95% confidence that the interval from the lower bound to the upper bound contains the true value of the population mean weight of newborn girls.

Outlines

00:00

📊 Calculating the Critical T Value for Confidence Intervals

This paragraph explains the process of determining the critical T value for a 95% confidence interval using a sample of 36 newborn girls' weights with a mean of 3216.7 grams and a standard deviation of 688.5 grams. The critical T value is calculated by finding the area in the right tail of the T distribution corresponding to the given confidence level, which is 0.025 after dividing the alpha value (0.05) by two. The degrees of freedom are determined by subtracting 1 from the sample size, resulting in 35. Using a statistical software, the critical T value is found to be 2.03 after rounding to two decimal places.

05:01

🔍 Finding the Margin of Error and Confidence Interval for Newborn Weights

The second paragraph details the calculation of the margin of error and the confidence interval for the population mean of newborn girls' weights. The margin of error is determined by multiplying the critical T value (2.03) by the sample standard deviation (688.5 grams) and then dividing by the square root of the sample size (36), resulting in a margin of error of 232.9 grams when rounded to one decimal place. The confidence interval is then calculated by adding and subtracting this margin of error from the sample mean, yielding a lower limit of 2983.8 grams and an upper limit of 3449.6 grams. The paragraph concludes with an interpretation of the confidence interval, stating that there is a 95% confidence that the interval contains the true population mean weight of newborn girls.

Mindmap

Keywords

💡Summary Statistics

Summary statistics are numerical values that summarize a dataset, such as the mean, median, mode, and standard deviation. In the video, summary statistics are used to describe the weights of newborn girls, providing a concise representation of the data's central tendency and dispersion.

💡Sample Size (n)

Sample size refers to the number of observations or elements in a sample. In this video, the sample size is 36, which is the number of newborn girls whose weights are being analyzed. The sample size is crucial for determining the reliability and generalizability of the statistical results.

💡Sample Mean (X bar)

The sample mean, denoted as X bar, is the average of the values in a sample. In the context of the video, the sample mean of 3216.7 grams represents the average weight of the newborn girls in the sample, serving as a central value for the dataset.

💡Sample Standard Deviation

The sample standard deviation is a measure of the amount of variation or dispersion in a set of values. In the video, a standard deviation of 688.5 grams indicates how much the weights of the newborn girls vary from the sample mean.

💡Confidence Level

The confidence level is the probability that the true population parameter lies within the calculated confidence interval. A 95% confidence level, as mentioned in the video, suggests that if the same sampling procedure were repeated many times, the interval would contain the true population mean in 95% of the cases.

💡Critical T Value

The critical T value is used in hypothesis testing to determine if the sample data provides sufficient evidence to reject the null hypothesis. In the video, the critical T value of 2.03 is calculated for a 95% confidence level with 35 degrees of freedom, which is used to calculate the margin of error.

💡Margin of Error

The margin of error represents the range within which the true population parameter is likely to fall, given the sample data. In the script, the margin of error is calculated as 232.9 grams, which is derived from the critical T value, the sample standard deviation, and the sample size.

💡Degrees of Freedom

Degrees of freedom in statistics refer to the number of values in the data set that are free to vary when calculating a statistic. In this video, the degrees of freedom are calculated as the sample size minus one (36 - 1 = 35), which is used in finding the critical T value.

💡Confidence Interval

A confidence interval is a range of values, derived from a sample, that is likely to contain the true population parameter. The video demonstrates how to calculate the confidence interval for the mean weight of newborn girls, which is given as 2983.8 grams to 3449.6 grams.

💡Normal Distribution

A normal distribution, also known as a Gaussian distribution, is a probability distribution that is characterized by a symmetrical bell-shaped curve. The video mentions that the sample is from a normally distributed population or is large enough (n > 30), which justifies the use of the t-distribution for the confidence interval calculation.

💡Interpretation of Confidence Interval

Interpreting a confidence interval involves understanding the probability that the interval contains the true population parameter. The video concludes with an interpretation that there is a 95% confidence that the interval from the lower to the upper bound contains the true mean weight of newborn girls.

Highlights

The sample size for the newborn girls' weights is 36.

The sample mean weight is 3216.7 grams.

The sample standard deviation is 688.5 grams.

A 95% confidence level is used for the analysis.

The critical T value for the margin of error is determined to be 2.03.

The degrees of freedom are calculated as 35.

The margin of error is calculated using the critical T value, sample standard deviation, and sample size.

The margin of error is found to be 232.9 grams.

The requirements for constructing a confidence interval are satisfied with a sample size greater than 30.

The confidence interval for the population mean weight is calculated.

The lower limit of the confidence interval is 2983.8 grams.

The upper limit of the confidence interval is 3449.6 grams.

The confidence interval estimate implies a 95% success rate in capturing the true population mean.

The interpretation of the confidence interval is explained in the context of the population mean weight of newborn girls.

The process involves using StatCrunch for calculating the critical T value and margin of error.

The importance of checking the requirements before constructing a confidence interval is emphasized.

The practical application of the confidence interval is in estimating the mean weight of newborn girls with a high degree of confidence.

Transcripts

Browse More Related Video

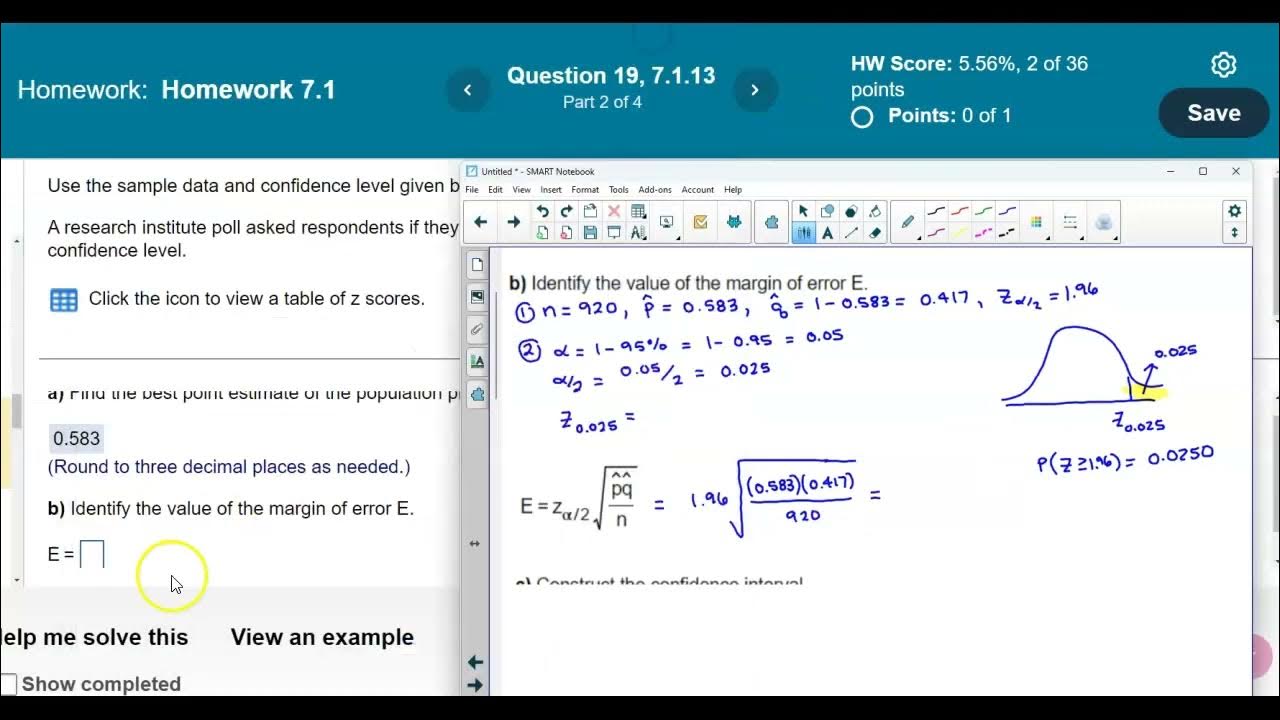
Math 14 7.1.13 Find the point estimate, margin of error & confidence interval of pop. proportion p.

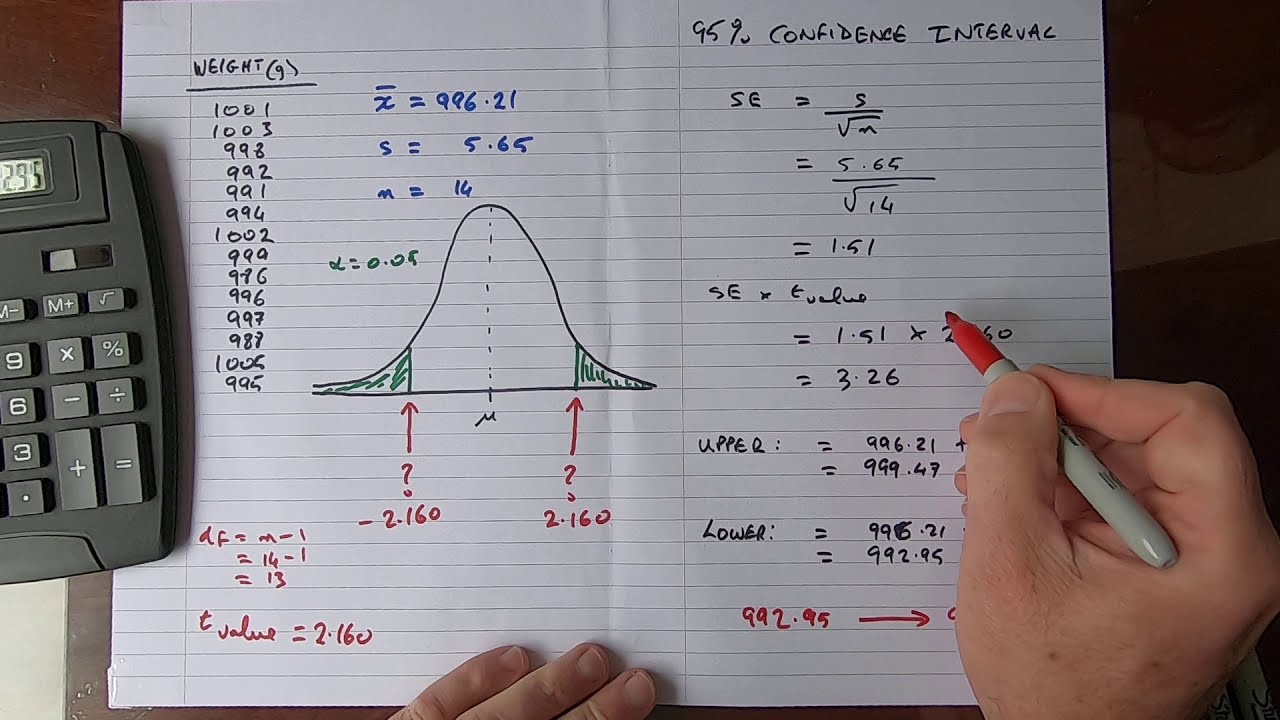
How To...Calculate the Confidence Interval for a Sample

Confidence Interval for a population mean - t distribution

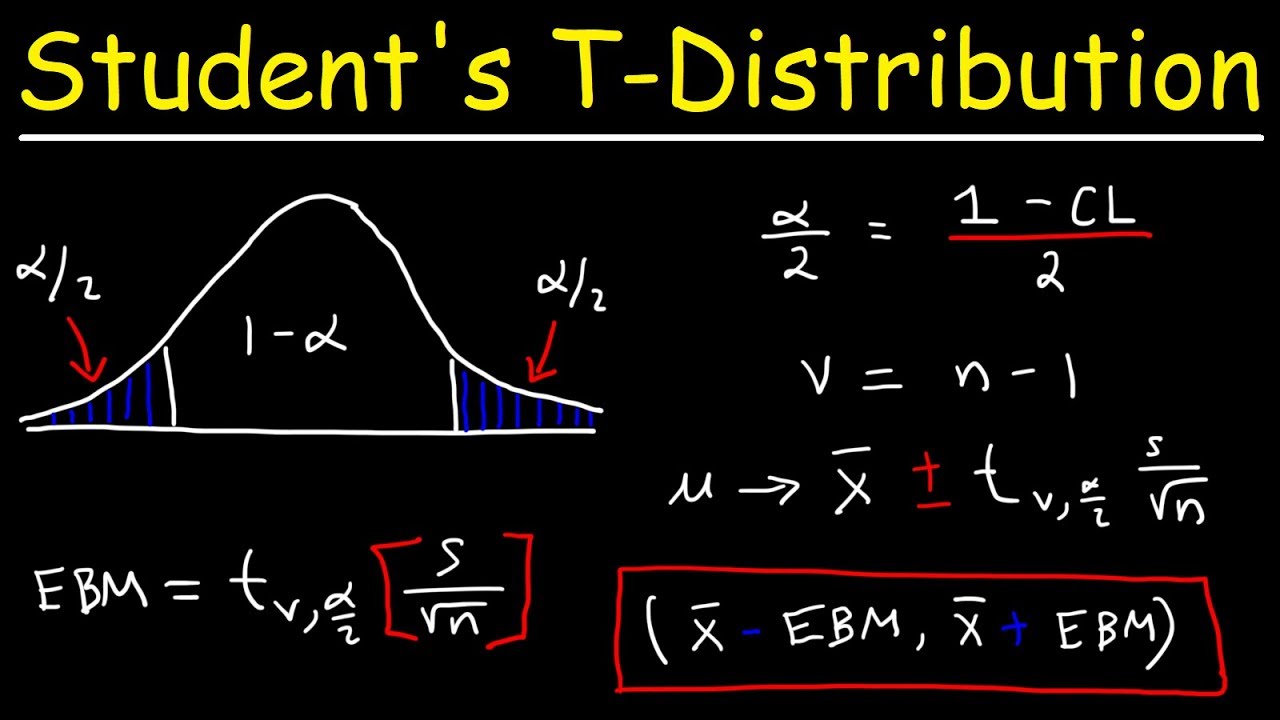
Student's T Distribution - Confidence Intervals & Margin of Error

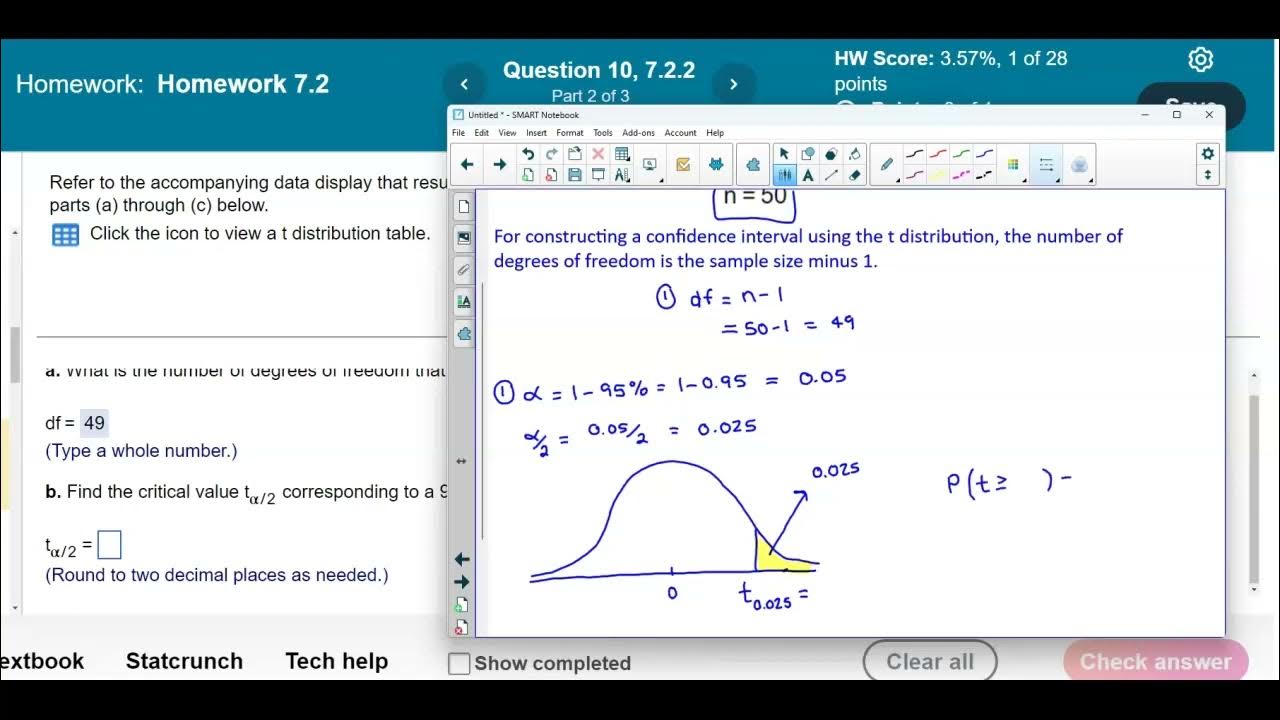
Math 14 HW 7.2.2 Find the degrees of freedom and critical t value.

Deriving a Confidence Interval for the Mean (The Rationale Behind the Confidence Interval Formula)

Math 14 HW 7.2.5-T Find critical t value, margin of error & confidence interval for population mean.

Takeaways

Q & A

What is the sample size (n) for the weights of newborn girls in the study?

What is the sample mean weight (X bar) of the newborn girls?

What is the sample standard deviation for the weights of the newborn girls?

What confidence level is used in the study?

How is the critical T value determined for the margin of error?

What is the critical T value obtained from the T distribution table?

How is the margin of error calculated in this study?

What is the calculated margin of error for the weights of the newborn girls?

What are the requirements for constructing a confidence interval to estimate a population mean?

What is the lower limit of the 95% confidence interval for the mean weight of newborn girls?

What is the upper limit of the 95% confidence interval for the mean weight of newborn girls?

How should the confidence interval be interpreted?